Tides
Tides are the rise and fall of sea levels due to the effects of the gravity exerted by the moon and the sun, and the rotation of the Earth.
learning objectives
- Explain factors that influence the times and amplitude of the tides at a locale
Tides are the rise and fall of sea levels due to the effects of gravitational forces exerted by the moon and the sun when combined with the rotation of the Earth. Tides occur to varying degrees and frequency, depending on location. Shorelines where two almost equally high tides and two low tides occur each day experience a semi- diurnal tide. The occurrence of only one high and one low tide each day is known as diurnal tide. A mixed tide referes to the daily occurrence of two uneven tides, or perhaps one high and one low tide. The times and amplitude of tides at various locales are influenced by the alignment of the sun and moon, the pattern of tides in the deep ocean, the shape of the coastline, and other forces.
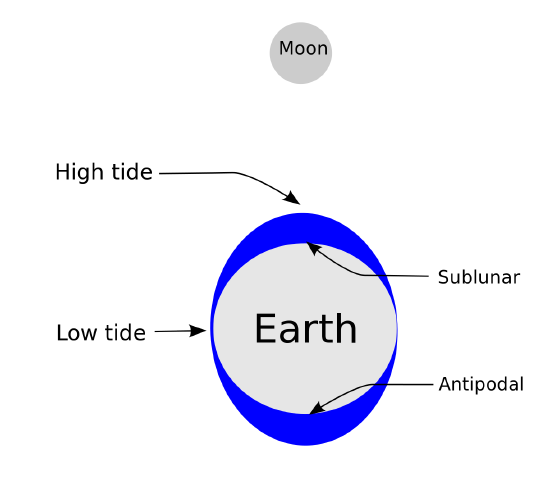
Earth’s tides.: Schematic of the lunar portion of earth’s tides showing (exaggerated) high tides at the sublunar and antipodal points for the hypothetical case of an ocean of constant depth with no land. There would also be smaller, superimposed bulges on the sides facing toward and away from the sun.
Tidal Force
If we want to know the acceleration “felt” by an observer living on Earth due to the moon, a tricky part is that the Earth is not an inertial frame of reference because it is in “free fall” with respect to the moon. Given this, in order to figure out the force observed, we must subtract the acceleration of the (Earth) frame itself. The tidal force produced by the moon on a small particle located on Earth is the vector difference between the gravitational force exerted by the moon on the particle, and the gravitational force that would be exerted if it were located at the Earth’s center of mass.
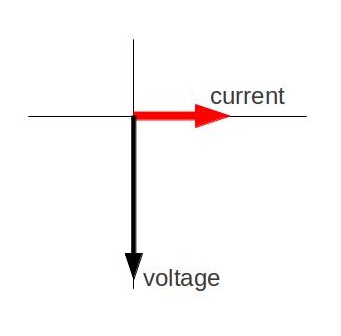
Moon’s Gravity on the Earth: Top picture shows the gravity force due to the Moon at different locations \(\mathrm{F_r}\) on Earth. Bottom picture shows the differential force \(\mathrm{F_r−F_{center}}\). This is the acceleration “felt” by an observer living on Earth.
As diagramed below, this is equivalent to subtracting the “red” vector from the “black” vectors on the surface of the Earth in the top picture, leading to the “differential” force represented by the bottom picture. Thus, the tidal force depends not on the strength of the lunar gravitational field, but on its gradient (which falls off approximately as the inverse cube of the distance to the originating gravitational body).
On average, the solar gravitational force on the Earth is 179 times stronger than the lunar, but because the sun is on average 389 times farther from the Earth its field gradient is weaker. The solar tidal force is 46% as large as the lunar. More precisely, the lunar tidal acceleration (along the moon-Earth axis, at the Earth’s surface) is about \(\mathrm{1.1⋅10^{−7}}\) g, while the solar tidal acceleration (along the sun-Earth axis, at the Earth’s surface) is about \(\mathrm{0.52⋅10^{−7}}\) g, where g is the gravitational acceleration at the Earth’s surface. Venus has the largest effect of the other planets, at 0.000113 times the solar effect.
Tidal Energy
Energy of tides can be extracted by two means: inserting a water turbine into a tidal current, or building ponds that release/admit water through a turbine. In the first case, the energy amount is entirely determined by the timing and tidal current magnitude, but the best currents may be unavailable because the turbines would obstruct ships. In the second case, impoundment dams are expensive to construct, natural water cycles are completely disrupted, as is ship navigation. However, with multiple ponds, power can be generated at chosen times. Presently, there are few installed systems for tidal power generation (most famously, La Rance by Saint Malo, France), as many difficulties are involved. Aside from environmental issues, simply withstanding corrosion and biological fouling pose engineering challenges.

Tidal Energy Generator: Tidal energy generator that works like a wind turbine, but with the ocean currents providing the energy. The circle in the middle is the turbine. The contraption travels up and down the two legs just like a lift and sits on the sea floor when in use.
Unlike with wind power systems, tidal power proponents point out that generation levels can be reliably predicted (save for weather effects). While some generation is possible for most of the tidal cycle, in practice, turbines lose efficiency at lower operating rates. Since the power available from a flow is proportional to the cube of the flow speed, the times during which high power generation is possible are brief.
The Coriolois Force
The Coriolis effect is a deflection of moving objects when they are viewed in a rotating reference frame.
learning objectives
- Formulate relationship between the Coriolis force, mass of an object, and speed in the rotating frame
The Coriolis effect is a deflection of moving objects when they are viewed in a rotating reference frame. In a reference frame with clockwise rotation, the deflection is to the left of the motion of the object; in one with counter-clockwise rotation, the deflection is to the right. Although recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave Coriolis, in connection with the theory of water wheels. Early in the 20th century, the term “Coriolis force” began to be used in connection with meteorology.

Frames of Reference: In the inertial frame of reference (upper part of the picture), the black object moves in a straight line. However, the observer (red dot) who is standing in the rotating/non-inertial frame of reference (lower part of the picture) sees the object as following a curved path due to the Coriolis and centrifugal forces present in this frame.
Newton’s laws of motion govern the motion of an object in a (non-accelerating) inertial frame of reference. When Newton’s laws are transformed to a uniformly rotating frame of reference, the Coriolis and centrifugal forces appear. Both forces are proportional to the mass of the object. The Coriolis force is proportional to the rotation rate, and the centrifugal force is proportional to its square. The Coriolis force acts in a direction perpendicular to the rotation axis and to the velocity of the body in the rotating frame. It is proportional to the object’s speed in the rotating frame. These additional forces are termed inertial forces, fictitious forces, or pseudo-forces. They allow the application of Newton’s laws to a rotating system. They are correction factors that do not exist in a non-accelerating or inertial reference frame.
Perhaps the most commonly encountered rotating reference frame is the Earth. The Coriolis effect is caused by the rotation of the Earth and the inertia of the mass experiencing the effect. Because the Earth completes only one rotation per day, the Coriolis force is quite small. Its effects generally become noticeable only for motions occurring over large distances and long periods of time, such as large-scale movements of air in the atmosphere or water in the ocean. Such motions are constrained by the surface of the earth, so generally only the horizontal component of the Coriolis force is important. This force causes moving objects on the surface of the Earth to be deflected in a clockwise sense (with respect to the direction of travel) in the northern hemisphere and in a counter-clockwise sense in the southern hemisphere. Rather than flowing directly from areas of high pressure to low pressure, as they would in a non-rotating system, winds and currents tend to flow to the right of this direction north of the equator and to the left of this direction south of it. This effect is responsible for the rotation of large cyclones.

Coriolis Force: This low-pressure system over Iceland spins counter-clockwise due to balance between the Coriolis force and the pressure gradient force.
Other Geophysical Applications
Tidal and Coriolis forces may not be obvious over a small time-space scale, but they are important in meteorology, navigation, and fishing.
learning objectives
- Identify fields that have to take into account the tidal and Coriolis forces
We have studied tidal and Coriolis forces previously. To review, the tidal force is responsible for the tides — it is a “differential force,” due to a secondary effect of the force of gravity. The Coriolis force is a fictitious force, representing a deflection of moving objects when they are viewed in a rotating reference frame of the Earth. Although their effects may not be obvious over a small time-space scale, these forces are important in such contexts as meteorology, navigation, fishing, and others.
The Tides
Tidal flows are important for marine navigation, and significant errors in position occur if they are not accounted for. Tidal heights are also important; for example, many rivers and harbors have a shallow “bar” at the entrance to prevent boats with significant draft from entering at low tide. Until the advent of automated navigation, competence in calculating tidal effects was important to naval officers. The certificate of examination for lieutenants in the Royal Navy once declared that the prospective officer was able to “shift his tides. ”

Tidal Indicator: Tidal Indicator, Delaware River, Delaware c. 1897. In the moment pictured, the tide is 1.25 feet above mean low water and is still falling, as indicated by the pointing of the arrow. The indicator is powered by a system of pulleys, cables, and a float
The Coriolis Force
The Coriolis force is quite small, and its effects generally become noticeable only when we are dealing with motions occurring over large distances and long periods of time, such as large-scale movements of air in the atmosphere or water in the ocean. The Coriolis effects also became important in ballistics calculations — for example, calculating the trajectories of very long-range artillery shells. The most famous historical example is the Paris gun, used by the Germans during World War I to bombard Paris from a range of about 120 km.
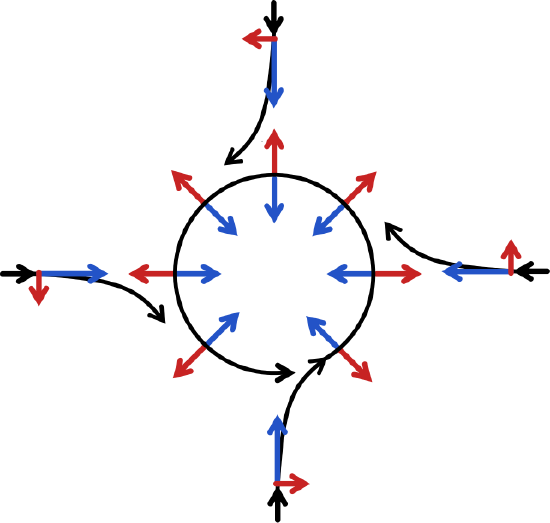
Flow Representation: A schematic representation of flow around a low-pressure area in the Northern Hemisphere. The pressure-gradient force is represented by blue arrows and the Coriolis acceleration (always perpendicular to the velocity) by red arrows









