Skip to main content
Physics LibreTexts

12.7: Kinetic Theory

  1. Last updated
  2. Save as PDF
  • Page ID
    18301

    • Boundless
    • Boundless
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    learning objectives

    • Express the relationship between the pressure and the average kinetic energy of gas molecules in the form of equation

    In Newtonian mechanics, if pressure is the force divided by the area on which the force is exerted, then what is the origin of pressure in a gas? What forces create the pressure? We can gain a better understanding of pressure (and temperature as well) from the kinetic theory of gases, which assumes that atoms and molecules are in continuous random motion.

    Microscopic Origin of Pressure

    Pressure is explained by kinetic theory as arising from the force exerted by molecules or atoms impacting on the walls of a container, as illustrated in the figure below. Consider a gas of N molecules, each of mass m, enclosed in a cubical container of volume V=L3. When a gas molecule collides with the wall of the container perpendicular to the x coordinate axis and bounces off in the opposite direction with the same speed (an elastic collision), then the momentum lost by the particle and gained by the wall (\(\mathrm{Δp}\)) is:

    image

    Translational Motion of Helium: Real gases do not always behave according to the ideal model under certain conditions, such as high pressure. Here, the size of helium atoms relative to their spacing is shown to scale under 1950 atmospheres of pressure.

    \[\begin{align} \mathrm{Δp} & \mathrm{=p_{i,x}−p_{f,x}=p_{i,x}−(−p_{i,x})} \\ & \mathrm{=2p_{i,x}=2mv_x} \end{align}\]

    where vx is the x-component of the initial velocity of the particle.

    The particle impacts one specific side wall once every \(\mathrm{Δt=\frac{2L}{v_x}}\),

    (where L is the distance between opposite walls). The force due to this particle is:

    \[\mathrm{F=\dfrac{Δp}{Δt}=\dfrac{mv_x^2}{L}.}\]

    The total force on the wall, therefore, is:

    \[\mathrm{F=\dfrac{Nm\bar{v^2_x}}L}\]

    where the bar denotes an average over the N particles. Since the assumption is that the particles move in random directions, if we divide the velocity vectors of all particles in three mutually perpendicular directions, the average value of the squared velocity along each direction must be same. (This does not mean that each particle always travel in 45 degrees to the coordinate axes. )

    image

    Pressure: Pressure arises from the force exerted by molecules or atoms impacting on the walls of a container.

    This gives \(\mathrm{\bar{v_x^2}=\frac{\bar{v^2}}{3}}\). We can rewrite the force as \(\mathrm{F=\frac{Nm\bar{v^2}}{3L}}\).

    This force is exerted on an area L2. Therefore the pressure of the gas is:

    \[\mathrm{P=\dfrac{F}{L^2}=\dfrac{Nm\bar{v^2}}{3V}=\dfrac{nm \bar{v^2}}{3},}\]

    where V=L3 is the volume of the box. The fraction n=N/V is the number density of the gas. This is a first non-trivial result of the kinetic theory because it relates pressure (a macroscopic property) to the average (translational) kinetic energy per molecule which is a microscopic property.

    Speed Distribution of Molecules

    A gas of many molecules has a predictable distribution of molecular speeds, known as the Maxwell-Boltzmann distribution.

    learning objectives

    • Describe the shape and temperature dependence of the Maxwell-Boltzmann distribution curve

    The motion of molecules in a gas is random in magnitude and direction for individual molecules, but a gas of many molecules has a predictable distribution of molecular speeds, known as the Maxwell-Boltzmann distribution (illustrated in ). The distribution has a long tail because some molecules may go several times the rms speed. The most probable speed vp (at the peak of the curve) is less than the rms speed vrms. As shown in, the curve is shifted to higher speeds at higher temperatures, with a broader range of speeds.

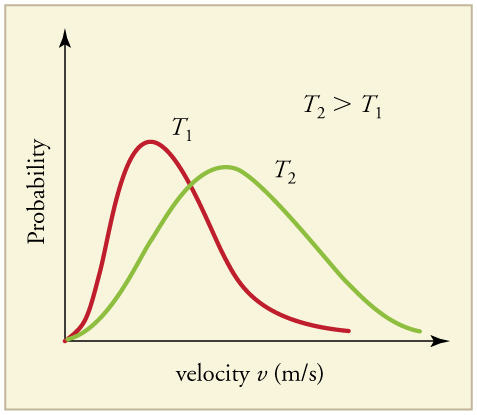
    image

    Maxwell-Boltzmann Distribution at Higher Temperatures: The Maxwell-Boltzmann distribution is shifted to higher speeds and is broadened at higher temperatures.

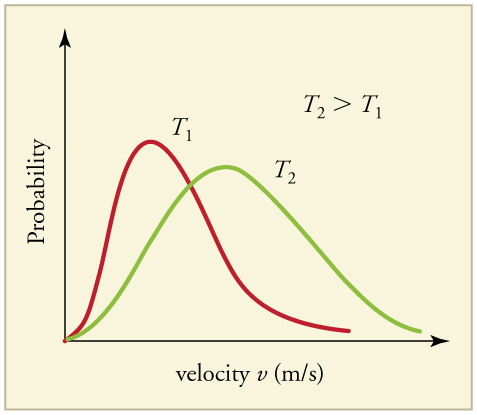
    image

    Maxwell-Boltzmann Distribution: The Maxwell-Boltzmann distribution of molecular speeds in an ideal gas. The most likely speed v_p is less than the rms speed v_rms. Although very high speeds are possible, only a tiny fraction of the molecules have speeds that are an order of magnitude greater than v_rms.

    Maxwell-Boltzmann Distribution

    Maxwell-Boltzmann distribution is a probability distribution. It applies to ideal gases close to thermodynamic equilibrium, and is given as the following equation:

    \[\mathrm{f_v(v_x,v_y,v_z)=(\dfrac{m}{2πkT})^{3/2} exp⁡[−\dfrac{m(v_x^2+v_y^2+v_z^2)}{2kT}],}\]

    where fv is the velocity probability density function. (Derivation of the formula goes beyond the scope of introductory physics. ) The formula calculates the probability of finding a particle with velocity in the infinitesimal element [dvx, dvy, dvz] about velocity v = [vx, vy, vz] is:

    \[\mathrm{f_v(v_x,v_y,v_z)dv_xdv_ydv_z.}\]

    It can also be shown that the Maxwell–Boltzmann velocity distribution for the vector velocity [vx, vy, vz] is the product of the distributions for each of the three directions:

    \[\mathrm{f_v(v_x,v_y,v_z)=f_v(v_x)f_v(v_y)f_v(v_z)}\]

    where the distribution for a single direction is,

    \[\mathrm{f_v(v_i)=\sqrt{\dfrac{m}{2πkT}} \; exp⁡[ \dfrac{−mv_i^2}{2kT}].}\]

    This makes sense because particles are moving randomly, meaning that each component of the velocity should be independent.

    Distribution for the Speed

    Usually, we are more interested in the speeds of molecules rather than their component velocities. The Maxwell–Boltzmann distribution for the speed follows immediately from the distribution of the velocity vector, above. Note that the speed is:

    \[\mathrm{v=\sqrt{v_x^2+v_y^2+v_z^2}}\]

    and the increment of volume is:

    \[\mathrm{dv_x \; dv_y \; dv_z=v^2 \sin ⁡ϕ \; dv \; dθ \; dϕ,}\]

    where \(\mathrm{θ}\) and \(\mathrm{ϕ}\) are the “course” (azimuth of the velocity vector) and “path angle” (elevation angle of the velocity vector). Integration of the normal probability density function of the velocity, above, over the course (from 0 to \(\mathrm{2π}\)) and path angle (from 0 to \(\mathrm{π}\)), with substitution of the speed for the sum of the squares of the vector components, yields the following probability density function (known simply as the Maxwell distribution):

    \(\mathrm{f(v)=\sqrt{(\frac{m}{2πkT})^3}4πv^2 \; exp⁡(\frac{−mv^2}{2kT})}\) for speed v.

    Temperature

    Temperature is directly proportional to the average translational kinetic energy of molecules in an ideal gas.

    learning objectives

    • Describe relationship between temperature and energy of molecules in an ideal gas

    Intuitively, hotter air suggests faster movement of air molecules. In this atom, we will derive an equation relating the temperature of a gas (a macroscopic quantity) to the average kinetic energy of individual molecules (a microscopic quantity). This is a basic and extremely important relationship in the kinetic theory of gases.

    Microscopic View

    We assume that a molecule is small compared with the separation of molecules in the gas (confined in a three dimensional container), and that its interaction with other molecules can be ignored. Also, we assume elastic collisions when molecules hit the wall of the container, as illustrated in.

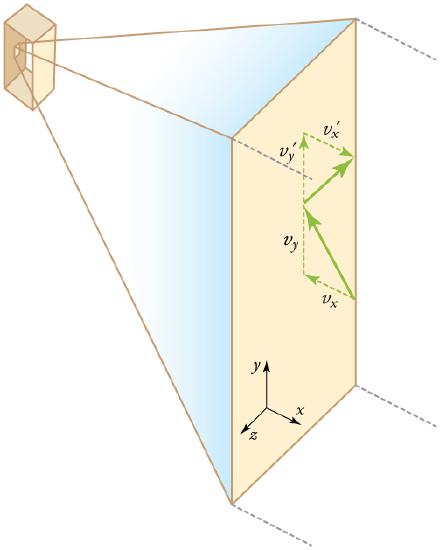
    image

    Elastic Collisions When Molecules Hit the Wall of the Container: Gas in a box exerts an outward pressure on its walls. A molecule colliding with a rigid wall has the direction of its velocity and momentum in the x-direction reversed. This direction is perpendicular to the wall. The components of its velocity momentum in the y- and z-directions are not changed, which means there is no force parallel to the wall.

    We have seen in the Atom on “Origin of Pressure ” that, for an ideal gas under our assumptions:

    \[\mathrm{P=\dfrac{Nm \bar{v^2}}{3V},}\]

    where P is the pressure, N is the number of molecules, m is the mass of the molecule, v is the speed of molecules, and V is the volume of the gas. From the equation, we get:

    \[\mathrm{PV=\dfrac{1}{3}Nm \bar{v^2} \; (Eq. 1).}\]

    What can we learn from this atomic and molecular version of the ideal gas law ? We can derive a relationship between temperature and the average translational kinetic energy of molecules in a gas. Recall the macroscopic expression of the ideal gas law:

    \[\mathrm{PV=NkT \; (Eq. 2),}\]

    where N is the number of molecules, T is the temperature of the gas, and k is the Boltzmann constant.

    Equating the right hand sides of the macroscopic and microscopic versions of the ideal gas law (Eq. 1 & 2) gives:

    \[\mathrm{\dfrac{1}{3}m\bar{v^2}=kT.}\]

    Thermal Energy

    Note that the average kinetic energy (KE) of a molecule in the gas is:

    \[\mathrm{\dfrac{1}{2}m\bar{v^2}.}\]

    Therefore, we derive the relation between average KE and temperature as follows:

    \[\mathrm{\bar{KE}=\dfrac{1}{2}m\bar{v^2}=\dfrac{3}{2}kT, \; (Eq. 3).}\]

    The average translational kinetic energy of a molecule is called thermal energy.

    RMS Speed

    Eq. 3 is a molecular interpretation of temperature. It has been found to be valid for gases and reasonably accurate in liquids and solids. It is another definition of temperature based on an expression of the molecular energy. It is sometimes useful to know the average speed of molecules in a gas in terms of temperature:

    \[\mathrm{\bar{v^2}=v_{rms}=\sqrt{\dfrac{3kT}{m}},}\]

    where vrms stands for root-mean-square (rms) speed.

    Internal Energy of an Ideal Gas

    Internal energy is the total energy contained by a thermodynamic system, and has two major components: kinetic energy and potential energy.

    learning objectives

    • Determine the number of degrees of freedom and calculate the internal energy for an ideal gas molecule

    In thermodynamics, internal energy is the total energy contained by a thermodynamic system. Internal energy has two major components: kinetic energy and potential energy. The kinetic energy is due to the motion of the system’s particles (e.g., translations, rotations, vibrations). In ideal gases, there is no inter-particle interaction. Therefore, we will disregard potential energy and only focus on the kinetic energy contribution to the internal energy.

    Monatomic Gases

    A monatomic gas is one in which atoms are not bound to each other. Noble gases (He, Ne, etc.) are typical examples. A helium balloon is shown in the following figure. In this case, the kinetic energy consists only of the translational energy of the individual atoms. Monoatomic particles do not vibrate, and their rotational energy can be neglected because atomic moment of inertia is so small. Also, they are not electronically excited to higher energies except at very high temperatures. Therefore, practical internal energy changes in an ideal gas may be described solely by changes in its translational kinetic energy.

    image

    Helium Blimp: Helium, like other noble gases, is a monatomic gas, which often can be described by the ideal gas law. It is the gas of choice to fill airships such as the Goodyear blimp.

    The average kinetic energy (KE) of a particle in an ideal gas is given as:

    \[\mathrm{\bar{KE}=\dfrac{1}{2}m\bar{v^2}=\dfrac{3}{2}kT,}\]

    where k is the Boltzmann’s constant. (See the Atom on “Temperature” in kinetic theory. ) With N atoms in the gas, its total internal energy U is given as:

    \[\mathrm{U=\dfrac{3}{2}NkT}\]

    where N is the number of atoms in the gas. Note that there are three degrees of freedom in monatomic gases: translation in x, y and z directions.

    Since atomic motion is random (and therefore isotropic), each degrees of freedom contribute \(\mathrm{\frac{1}{2}kT}\) per atom to the internal energy.

    Diatomic gases

    A diatomic molecule (H2, O2, N2, etc.) has 5 degrees of freedom (3 for translation in x, y and z directions, and 2 for rotation). Therefore, the internal energy for diatomic gases is \(\mathrm{U=\frac{5}{2}NkT.}\)

    Key Points

    • We can gain a better understanding of pressure (and temperature as well) from the kinetic theory of gases, which assumes that atoms and molecules are in continuous random motion.
    • Pressure, a macroscopic property, can be related to the average (translational) kinetic energy per molecule which is a microscopic property by \(\mathrm{P=\frac{nm\bar{v^2}}{3}}\).
    • Since the assumption is that the particles move in random directions, the average value of velocity squared along each direction must be same. This gives: \(\mathrm{\bar{v_x^2}=\bar{v_y^2}=\bar{v_z^2}=\bar{v^2}/3}\).
    • The Maxwell-Boltzmann distribution has a long tail, and the most probable speed vp is less than the rms speed vrms. The distribution curve is shifted to higher speeds at higher temperatures, with a broader range of speeds.
    • Maxwell-Boltzmann distribution is given as follows: \(\mathrm{f_v(v_x,v_y,v_z)=(\frac{m}{2πkT})^{3/2} \; exp⁡[−\frac{m(v_x^2+v_y^2+v_z^2)}{2kT}]}\). It is a product of three independent 1D Maxwell-Boltzmann distributions.
    • Molecular speed distribution is given as \(\mathrm{f(v)=\sqrt{(\frac{m}{2πkT})^3}4πv^2 \; exp⁡(\frac{−mv^2}{2kT})}\). This is simply called Maxwell distribution.
    • The average translational kinetic energy of a molecule is equivalent to \(\mathrm{\frac{3}{2}kT}\) and is called thermal energy.
    • In kinematic theory of gases, macroscopic quantities (such as press and temperature) are explained by considering microscopic (random) motion of molecules.
    • The rms speed of molecules in a gas is given as \(\mathrm{\sqrt{\frac{3kT}{m}}}\).
    • In ideal gases, there is no inter-particle interaction. Therefore, only the kinetic energy contribute to the internal energy.
    • Each degrees of freedom contribute \(\mathrm{\frac{1}{2}kT}\) per atom to the internal energy.
    • For monatomic ideal gases with N atoms, its total internal energy U is given as \(\mathrm{U=\frac{3}{2}NkT}\). For diatomic gases, \(\mathrm{U=\frac{5}{2}NkT}\).

    Key Terms

    • kinetic theory of gases: The kinetic theory of gases describes a gas as a large number of small particles (atoms or molecules), all of which are in constant, random motion.
    • Newtonian mechanics: Early classical mechanics as propounded by Isaac Newton, especially that based on his laws of motion and theory of gravity.
    • rms: Root mean square: a statistical measure of the magnitude of a varying quantity.
    • ideal gas: A hypothetical gas whose molecules exhibit no interaction and undergo elastic collision with each other and with the walls of the container.
    • Boltzmann’s constant: The physical constant relating energy at the particle level with temperature observed at the bulk level. It is the gas constant R divided by Avogadro’s number, NA.
    • moment of inertia: A measure of a body’s resistance to a change in its angular rotation velocity
    • noble gas: Any of the elements of group 18 of the periodic table, being monatomic and (with very limited exceptions) inert.

    LICENSES AND ATTRIBUTIONS

    CC LICENSED CONTENT, SHARED PREVIOUSLY

    CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

    This page titled 12.7: Kinetic Theory is shared under a not declared license and was authored, remixed, and/or curated by Boundless.