14.6: Heat Capacities of an Ideal Gas

Last updated
Save as PDF

Page ID: 18319

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Learning Objectives

By the end of this section, you will be able to:

Define heat capacity of an ideal gas for a specific process
Calculate the specific heat of an ideal gas for either an isobaric or isochoric process
Explain the difference between the heat capacities of an ideal gas and a real gas
Estimate the change in specific heat of a gas over temperature ranges

We learned about specific heat and molar heat capacity previously; however, we have not considered a process in which heat is added. We do that in this section. First, we examine a process where the system has a constant volume, then contrast it with a system at constant pressure and show how their specific heats are related.

Let’s start with looking at Figure \(\PageIndex{1}\), which shows two vessels A and B, each containing 1 mol of the same type of ideal gas at a temperature T and a volume V. The only difference between the two vessels is that the piston at the top of A is fixed, whereas the one at the top of B is free to move against a constant external pressure p. We now consider what happens when the temperature of the gas in each vessel is slowly increased to \(T + dT\) with the addition of heat.

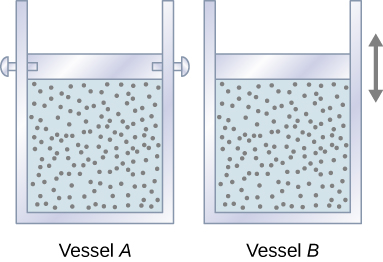
Two containers, labeled Vessel A and Vessel B, are shown. Both are filled with gas and are capped by a piston. In vessel A, the piston is pinned in place. In vessel B, the piston is free to slide, as indicated by a double headed arrow near the piston. — Figure \(\PageIndex{1}\): Two vessels are identical except that the piston at the top of A is fixed, whereas that atop B is free to move against a constant external pressure p.

Since the piston of vessel A is fixed, the volume of the enclosed gas does not change. Consequently, the gas does no work, and we have from the first law

\[dE_{int} = dQ - dW = dQ.\]

We represent the fact that the heat is exchanged at constant volume by writing

\[dQ = C_VndT,\] where \(C_V\) is the molar heat capacity at constant volume of the gas. In addition, since \(dE_{int} = dQ\) for this particular process,

\[dE_{int} = C_VndT. \label{3.9}\]

We obtained this equation assuming the volume of the gas was fixed. However, internal energy is a state function that depends on only the temperature of an ideal gas. Therefore, \(dE_{int} = C_VndT\) gives the change in internal energy of an ideal gas for any process involving a temperature change dT.

When the gas in vessel B is heated, it expands against the movable piston and does work \(dW = pdV\). In this case, the heat is added at constant pressure, and we write \[dQ = C_{p}ndT,\] where \(C_p\) is the molar heat capacity at constant pressure of the gas. Furthermore, since the ideal gas expands against a constant pressure,

\[d(pV) = d(RnT)\] becomes \[pdV = RndT.\]

Finally, inserting the expressions for dQ and pdV into the first law, we obtain

\[dE_{int} = dQ - pdV = (C_{p}n - Rn)dT.\]

We have found \(dE_{int}\) for both an isochoric and an isobaric process. Because the internal energy of an ideal gas depends only on the temperature, \(dE_{int}\) must be the same for both processes. Thus,

\[C_{V}ndT = (C_{p}n - Rn)dT,\]

and

\[C_p = C_V + R. \label{eq50}\]

The derivation of Equation \ref{eq50} was based only on the ideal gas law. Consequently, this relationship is approximately valid for all dilute gases, whether monatomic like He, diatomic like \(O_2\), or polyatomic like \(CO_2\) or \(NH_3\).

In the preceding chapter, we found the molar heat capacity of an ideal gas under constant volume to be

\[C_V = \dfrac{d}{2}R,\]

where d is the number of degrees of freedom of a molecule in the system. Table \(\PageIndex{1}\) shows the molar heat capacities of some dilute ideal gases at room temperature. The heat capacities of real gases are somewhat higher than those predicted by the expressions of \(C_V\) and \(C_p\) given in Equation \ref{eq50}. This indicates that vibrational motion in polyatomic molecules is significant, even at room temperature. Nevertheless, the difference in the molar heat capacities, \(C_p - C_V\), is very close to R, even for the polyatomic gases.

Table \(\PageIndex{1}\): Molar Heat Capacities of Dilute Ideal Gases at Room Temperature
		\(C_p\)	\(C_V\)	\(C_p - C_V\)
Type of Molecule	Gas	(J/mol K)	(J/mol K)	(J/mol K)
Monatomic	Ideal	\(\frac{5}{2}R = 20.79\)	\(\frac{3}{2}R = 12.47\)	\(R = 8.31\)
Diatomic	Ideal	\(\frac{7}{2}R = 29.10\)	\(\frac{5}{2}R = 20.79\)	\(R = 8.31\)
Polyatomic	Ideal	\(4R = 33.26\)	\(3R = 24.04\)	\(R = 8.31\)

Glossary


molar heat capacity at constant pressure: quantifies the ratio of the amount of heat added removed to the temperature while measuring at constant pressure
molar heat capacity at constant volume: quantifies the ratio of the amount of heat added removed to the temperature while measuring at constant volume