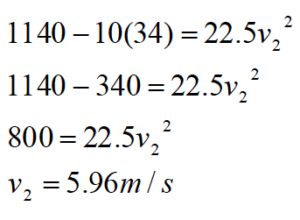2.3: Conservation Laws
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conservation Laws
Concepts and Principles
The Impulse-Momentum Relation
Just like the kinematic relations and Newton’s second law, the impulse-momentum relation is independently valid in any member of a set of perpendicular directions. Thus, we will typically apply the impulse-momentum relation in its component forms:

The Work-Energy Relation
From Model 1, our expression for the Work-Energy Relation, with gravitational potential energy terms, is:

It’s very important to remember that the work-energy relation is a scalar equation, meaning it cannot be broken into components and “solved” separately in the x-, y-, and z-directions. This is even more important to remember now that we are working in multiple dimensions. This observation results in two important points:
- The work-energy relation involves the actual initial and final velocities, not their components. The kinetic energy of an object does not depend on the direction of travel of the object.
- In the expression for work,
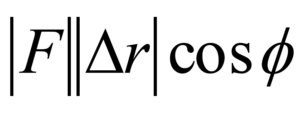 , the product of the magnitude of the force and the magnitude of the displacement is multiplied by cos
, the product of the magnitude of the force and the magnitude of the displacement is multiplied by cos  , where
, where  is defined to be the angle between the applied force and the displacement of the object. If the force and displacement are in the same direction
is defined to be the angle between the applied force and the displacement of the object. If the force and displacement are in the same direction  = 0°, and the work is positive (the object gains energy). If the force and displacement are in the opposite direction
= 0°, and the work is positive (the object gains energy). If the force and displacement are in the opposite direction  = 180°, and the work is negative (the object loses energy). If the force and displacement are perpendicular, no work is done. Note that the actual directions of the force and the displacement are unimportant, only their directions relative to each other affect the work.
= 180°, and the work is negative (the object loses energy). If the force and displacement are perpendicular, no work is done. Note that the actual directions of the force and the displacement are unimportant, only their directions relative to each other affect the work.
Analysis Tools
Applying the Impulse-Momentum Relation to a Single Object
Let’s investigate the following scenario:
A boy pulls a 30 kg sled, including the mass of his kid brother, along ice. The boy pulls on the tow rope, oriented at 600 above horizontal, with a force of 110 N until his kid brother begins to cry. Like clockwork, his brother always cries upon reaching a speed of 2.0 m/s. The frictional coefficient is (0.20,0.15).

To apply the impulse-momentum relation, you must clearly specify the initial and final events at which you will tabulate the momentum. For example:
| Event 1: The instant before the sled begins to move.
P1x = 0 P1y = 0 | Event 2: The instant the sled reaches 2.0 m/s
P2x = 30 (2.0) = 60 P2y = 0 |

Applying impulse-momentum separately in the x- and y-directions yields:

Substituting the value for the force of the surface into the x-equation,

The kid brother begins to cry after only 2.4 s.
Applying the Work-Energy Relation to a Single Object
What will the work-energy relation tell us about the same scenario?
A boy pulls a 30 kg sled, including the mass of his kid brother, along ice. The boy pulls on the tow rope, oriented at 600 above horizontal, with a force of 110 N until his kid brother begins to cry. Like clockwork, his brother always cries upon reaching a speed of 2.0 m/s. The frictional coefficient is (0.20,0.15).

To apply the work-energy relation, you must clearly specify the initial and final events at which you will tabulate the energy. For example:
| Event 1: The instant before the sled begins to move.
KE1 = 0 GE1 = 0 | Event 2: The instant the sled reaches 2.0 m/s
KE2 = ½ 30 (2.0)2 = 60 GE2 = 0 |
Applying the work-energy relation yields:

Notice that the force of the surface does no work, the force of the rope does positive work, and the force of friction does negative work. Each of these terms should make sense if you remember that work is the transfer of energy into (positive) or out of (negative) the system of interest. Also recall that in this form of the work-energy relation we conceptualize gravity as a source of potential energy, not as a force that does work.
Using the result for the force of the surface determined in the first example, Fsurface = 199 N, gives:

The kid brother begins to cry after traveling 2.4 m.
Applying Work-Energy with Gravitational Potential Energy
Let’s use the work-energy relation, with gravitational potential energy terms, to analyze the following scenario:
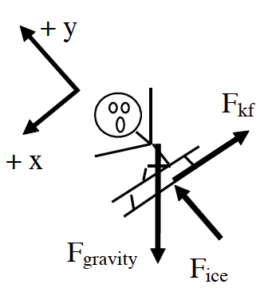
A 30 kg child on his 15 kg sled slides down his parents’ 10 m long, 150 above horizontal driveway after an ice storm. The coefficient of friction between the sled and the driveway is (0.10, 0.08).
To calculate the gravitational energy terms let the bottom of the driveway be zero and up positive. The coordinate system used to calculate gravitational energy does not in general have to be the same as the system you use for the rest of the problem. In fact, since the work-energy relation is a scalar equation, the other portions of the equation should not depend on your choice of coordinate system at all!
| Event 1: The instant before the sled begins to move.
KE1 = 0 GE1 = 45 (9.8) (10 sin150) = 1140 | Event 2: The instant the sled reaches the bottom of the driveway
KE2 = ½ 45 v2 GE2 = 0 |
 | 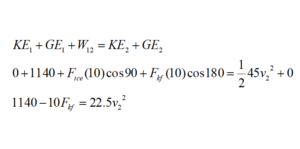 |
Note:
- The only forces that could do work are the force of the ice and the force of friction, since the action of the force of gravity is already incorporated into the gravitational potential energy terms.
- The heights in the gravitational potential energy function were measured from the bottom of the driveway, with the positive direction as upward, as required. Notice that the initial height is not the same as the length of the driveway. Since the driveway is 10 m long, at an angle of 15°, the height of the top of the driveway relative to the bottom is (10 m) sin 15°. The height at the bottom of the driveway is defined to be 0 m.
To finish the analysis we need to determine the kinetic frictional force. Since this depends on the force of the ice, apply Newton’s Second Law in the y-direction and find:

Plugging this value into the work-energy relation yields:
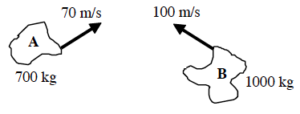
A Two-Dimensional Collision
Let’s try a two-dimensional collision.
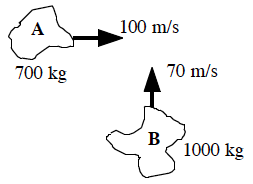
At a busy intersection, an impatient driver heading south runs a red-light and collides with a delivery truck originally moving at 15 m/s west. The vehicles become entangled and the skid marks from the wreckage are at 22o south of west. The auto mass is 755 kg and the truck mass is 1250 kg.
Partial free-body diagrams (top view) for both the car and the truck during the time interval during the collision are shown below.

These are only partial free-body diagrams because:
- Forces perpendicular to the earth’s surface (the force of gravity and the force of the road) are not shown.These are only partial free-body diagrams because:
- During a collision, the force between the colliding objects is normally much greater in magnitude than any other forces acting on the objects. Therefore we will often ignore the other forces acting on colliding objects for the duration of a collision. This approximation is termed the impulse approximation. Under the impulse approximation, the frictional forces between the car and truck and the road are ignored.
Also note that the direction of the force acting between the car and truck is unknown. The angle q is not determined from the situation description.
| Event 1: The instant before the car and truck collide
Object: Car P1x = 0 P1y = 755 vcar | Event 2: The instant they reach a common velocity
P2x = 755 (v2 cos 22º) = 700 v2 P2y = 755 (v2 sin 22º) = 283 v2 |

| Object: Truck P1x = 1250 (15) = 18750 P1y = 0 | P2x = 1250 (v2 cos 22º) = 1160 v2 P2y = 1250 (v2 sin 22º) = 468 v2 |

Applying the impulse-momentum relation to the car and truck yields:
Car

Truck

Since the magnitude of the force on the car due to the truck and the force on the truck due to the car are equal, when the x-equations for the car and truck are added, the impulses cancel!

This is the speed of the wreckage immediately after the collision. Note that this is exactly the same equation we would have written if we had considered the system of the car and truck right from the start. Try it!
Adding the two y-equations yields:

This is the speed of the car immediately before colliding with the truck.
Activities
Below are six different directions in which a baseball can be thrown. In all cases the baseball is thrown at the same initial speed from the same height above the ground. Assume the effects of air resistance are negligible.

Rank these baseballs on the basis of their horizontal speed the instant before they hit the ground.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Rank these baseballs on the basis of their vertical speed the instant before they hit the ground.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Rank these baseballs on the basis of their speed the instant before they hit the ground.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your rankings:
Below are six different directions and heights from which a baseball can be thrown. In all cases the baseball is thrown at the same speed, v. Assume the effects of air resistance are negligible.

Rank these baseballs on the basis of their speed the instant before they hit the ground.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
A crate is released from rest along an inclined surface. The mass of the crate and the angle of the incline vary. The frictional coefficients between the crates and the surfaces are identical and so small that the effect of friction is negligible. All crates are released from the same vertical height, H, above the bottom of the incline.

Rank these scenarios on the basis of the kinetic energy of the crate the instant it reaches the bottom of the incline.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Rank these scenarios on the basis of the speed of the crate the instant it reaches the bottom of the incline.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
A crate is released from rest along an inclined surface. The mass of the crate and the angle of the incline vary. The frictional coefficients between the crates and the surfaces are identical and so small that the effect of friction is negligible. All crates are released from the same distance, D, along the incline.

Rank these scenarios on the basis of the kinetic energy of the crate the instant it reaches the bottom of the incline.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Rank these scenarios on the basis of the speed of the crate the instant it reaches the bottom of the incline.
Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are bird’s-eye views of six automobile crashes an instant before they occur. The automobiles have different masses and velocities. All automobiles will remain joined together after the impact and skid to rest. Rank these automobile crashes on the basis of the angle at which the wreckage skids. Let 00 be the angle oriented directly toward the right and measure angles counterclockwise from 00.

Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
Below are bird’s-eye views of six automobile crashes an instant before they occur. The automobiles have different masses and velocities. All automobiles will remain joined together after the impact and skid to rest at the same angle, as measured from a line oriented directly toward the right. Rank these scenarios on the basis of the initial speed of the auto traveling toward the top of the page.

Largest 1. _____ 2. _____ 3. _____ 4. _____ 5. _____ 6. _____ Smallest
_____ The ranking cannot be determined based on the information provided.
Explain the reason for your ranking:
For each of the collisions illustrated below, sketch a graph of the momentum of asteroid A, the momentum of asteroid B, and the total momentum in the system of the two asteroids. Sketch the horizontal and vertical momentum separately. Begin your graph before the collision takes place and continue it after the collision is over. Use a consistent scale on all graphs.
| a. The two asteroids remain joined together after the collision.
|
| b. The two asteroids remain joined together after the collision.
|
For each of the collisions illustrated below, sketch a graph of the momentum of asteroid A, the momentum of asteroid B, and the total momentum in the system of the two asteroids. Sketch the horizontal and vertical momentum separately. Begin your graph before the collision takes place and continue it after the collision is over. The asteroids’ initial velocities are both oriented at the same angle from horizontal. Use a consistent scale on all graphs.
| a. The two asteroids remain joined together after the collision.
|
| b. The two asteroids remain joined together after the collision.
|
For each of the collisions illustrated below, sketch a graph of the momentum of asteroid A, the momentum of asteroid B, and the total momentum in the system of the two asteroids. Sketch the horizontal and vertical momentum separately. Begin your graph before the collision takes place and continue it after the collision is over.
| a. The two asteroids remain joined together after the collision and move directly toward the top of the page.
|
| b. The two asteroids remain joined together after the collision and move directly toward the right. The asteroids’ initial velocities are both oriented at the same angle from horizontal.
|
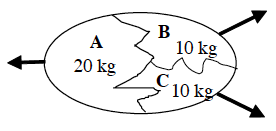
For each of the explosions illustrated below, sketch a graph of the momentum of fragment A, B, and C, and the total momentum in the system of the three asteroids. Sketch the horizontal and vertical momentum separately. Begin your graph before the explosion takes place and continue it as the fragments move apart. The exploding egg is initially at rest.
| a. Fragment A moves horizontally and fragments B and C move at the same angle from horizontal after the explosion.
|
| b. Fragment B moves vertically and fragments A and C move at the same angle from vertical after the explosion.
|
For each of the scenarios described below, indicate the amount of kinetic energy and gravitational potential energy of the object at each of the events listed. Use a consistent scale throughout both motions. Set ground level as the zero-point of gravitational potential energy
a. A baseball is thrown at 30 m/s at an angle of 30 ° above horizontal over level ground.
b. A baseball is thrown at 30 m/s at an angle of 60 ° above horizontal over level ground.
For each of the scenarios described below, indicate the amount of kinetic energy and gravitational potential energy of the object at each of the events listed. Use a consistent scale throughout both motions.
a. A 60 kg skier starts from rest at the top of a 100 m, 250 slope. He doesn’t push with his poles because he’s afraid of going too fast. Set the bottom of the slope as the zero-point of gravitational potential energy.
b. A 60 kg skier starts from rest at the top of a 100 m, 250 slope. He doesn’t push with his poles because he’s afraid of going too fast. Set the top of the slope as the zero-point of gravitational potential energy.
For each of the scenarios described below, indicate the amount of kinetic energy and gravitational potential energy of each object at each of the events listed. Use a consistent scale throughout both motions. Set the initial positions of the skier and block as the zero-points of gravitational potential energy
a. In a horizontal skiing device, the skier begins from rest 35 m from the end of the skiing run. The ballast block has a mass of 50 kg and the skier has a mass of 75 kg. The coefficient of friction is extremely small.
b. In an inclined skiing device, the skier begins from rest 35 m from the end of the 200 above horizontal inclined skiing run. The ballast block has a mass of 50 kg and the skier has a mass of 75 kg. The coefficient of friction is extremely small.
A girl pulls a 35 kg sled, including the mass of her kid sister, along ice. The girl pulls on the tow rope, oriented at 400 above horizontal, with a force of 120 N until her sister begins to cry. Like clockwork, her sister always cries upon reaching a speed of 3.0 m/s. The frictional coefficient is (0.10,0.08).
| Free-Body Diagram
| Mathematical Analysis[i]
Event 1:
P1x = P1y = J12x = J12y =
KE1 = GE1 = W12 = |
Event 2:
P2x = P2y =
KE2 = GE2 =
|
a. How far has the sled moved before the little sister begins to cry?
b. What is the elapsed time before the little sister begins to cry?
A boy pulls a 30 kg sled, including the mass of his kid brother, along ice. The boy pulls on the tow rope, oriented at 60° above horizontal, with a force of 110 N for 3.0 s. At the end of the 3.0 s pull, his kid brother begins to cry. The frictional coefficient is (0.20,0.15).
| Free-Body Diagram
| Mathematical Analysis[ii]
Event 1:
P1x = P1y = J12x = J12y =
KE1 = GE1 = W12 = |
Event 2:
P2x = P2y =
KE2 = GE2 =
|
a. How fast is the sled moving before the little brother begins to cry?
b. How far has the sled moved before the little brother begins to cry?
Starting from rest, a girl can pull a sled, carrying her kid brother, 20 m in 8 s. The girl pulls on the tow rope, oriented at 300 above horizontal, with a force of 90 N. The frictional coefficient is (0.15,0.10).
| Free-Body Diagram
| Mathematical Analysis[iii]
Event 1:
P1x = P1y = J12x = J12y =
KE1 = GE1 = W12 = |
Event 2:
P2x = P2y =
KE2 = GE2 =
|
A 100 kg bicycle and rider initially move at 16 m/s up a 150 hill. The rider slams on the brakes and skids to rest. The coefficient of friction is (0.8,0.7).
| Free-Body Diagram
| Mathematical Analysis[iv]
Event 1:
P1x = P1y = J12x = J12y =
KE1 = GE1 = W12 = |
Event 2:
P2x = P2y =
KE2 = GE2 =
|
How far does the bike skid?
What is the elapsed time before the bike stops skidding?
A 60 kg skier starts from rest at the top of a 100 m, 250 slope. He doesn’t push with his poles because he’s afraid of going too fast. The frictional coefficient is (0.10,0.05).
| Free-Body Diagram
| Mathematical Analysis[v]
Event 1:
P1x = P1y = J12x = J12y =
KE1 = GE1 = W12 = |
Event 2:
P2x = P2y =
KE2 = GE2 =
|
A 70 kg snowboarder starts from rest at the top of a 270 m, 200 slope. At the bottom of the hill she’s moving at 33 m/s.
| Free-Body Diagram
| Mathematical Analysis[vi]
Event 1:
P1x = P1y = J12x = J12y =
KE1 = GE1 = W12 = |
Event 2:
P2x = P2y =
KE2 = GE2 =
|
| The device at right guarantees all the excitement of skiing without the need for hills. The skier begins from rest 35 m from the brick wall. The block has a mass of 50 kg and the skier has a mass of 75 kg. The coefficient of friction is (0.15,0.13). | 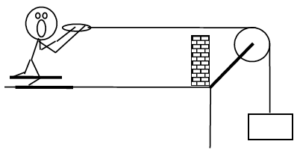 |
Free-Body Diagrams Mathematical Analysis[vii]
| skier | block
| Event 1:
Object: KE1 = GE1 = W12 =
Object: KE1 = GE1 = W12 = | Event 2:
KE2 = GE2 =
KE2 = GE2 =
|
| The device at right allows novices to ski downhill at reduced speeds. The block has a mass of 10 kg and the skier has a mass of 80 kg. The coefficient of friction is (0.08,0.07). The skier starts from rest at the top of a 30 m, 200 slope. | 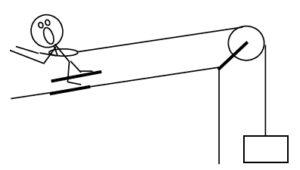 |
Free-Body Diagrams Mathematical Analysis[viii]
| skier | block
| Event 1:
Object: KE1 = GE1 = W12 =
Object: KE1 = GE1 = W12 = | Event 2:
KE2 = GE2 =
KE2 = GE2 =
|
| The device at right allows you to ski uphill (until you smash into the pulley). The ballast block has a mass of 60 kg and the skier has a mass of 70 kg. The coefficient of friction is (0.1,0.09). The ramp is inclined at 200 above horizontal and the pulley is 45 m away. | 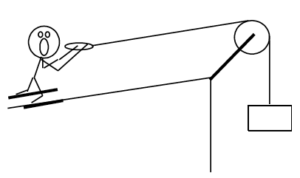 |
Free-Body Diagrams Mathematical Analysis[ix]
| skier | block
| Event 1:
Object: KE1 = GE1 = W12 =
Object: KE1 = GE1 = W12 = | Event 2:
KE2 = GE2 =
KE2 = GE2 =
|
Two identical 800 kg automobiles, one moving east at 10 m/s and the other moving north at 15 m/s, collide. After the collision they remain joined together and move with a common velocity.
Free-Body Diagrams Mathematical Analysis[x]
| Event 1:
Object: P1x = P1y = J12x = J12y =
Object: P1x = P1y = J12x = J12y =
| Event 2:
P2x = P2y =
P2x = P2y =
|
Two identical 750 kg automobiles, one moving east at 10 m/s and the other moving north, collide. After the collision they remain joined together and move with a common velocity. The wreckage skids at 300 north of east.
Free-Body Diagrams Mathematical Analysis[xi]
| Event 1:
Object: P1x = P1y = J12x = J12y =
Object: P1x = P1y = J12x = J12y =
| Event 2:
P2x = P2y =
P2x = P2y =
|
In a demolition derby, a 700 kg Audi is traveling at 15 m/s 300 north of east. An 800 kg BMW is traveling at 5.0 m/s south. They collide. After the collision, the Audi is redirected to 100 north of east and the BMW is redirected to 400 east of south.
Free-Body Diagrams Mathematical Analysis[xii]
| Event 1:
Object: P1x = P1y = J12x = J12y =
Object: P1x = P1y = J12x = J12y =
| Event 2:
P2x = P2y =
P2x = P2y =
|
In a demolition derby, a 600 kg Audi is traveling at 15 m/s 300 west of south. A 700 kg BMW is traveling at 10 m/s 400 north of east. They collide. After the collision, the Audi is redirected to 200 north of west and the BMW is redirected to 500 south of east.
Free-Body Diagrams Mathematical Analysis[xiii]
| Event 1:
Object: P1x = P1y = J12x = J12y =
Object: P1x = P1y = J12x = J12y =
| Event 2:
P2x = P2y =
P2x = P2y =
|
A boy pulls an initially stationary sled of mass m (including the mass of the strange neighborhood kid riding the sled) along a level surface. He exerts a force of magnitude F at an angle of q above the horizontal. Determine the velocity (v) of the sled as a function of the distance pulled (d), the appropriate coefficient of friction between the sled and the surface, m, F, q , and g.
| Free-Body Diagram
| Mathematical Analysis
Event 1:
KE1 = GE1 = W12 = |
Event 2:
KE2 = GE2 =
|
Questions
If d = 0 m, what should v equal? Does your function agree with this observation?
If m = 0 kg, what should v equal? Does your function agree with this observation?
If F = 0 N, what should v equal? Does your function agree with this observation?
A skier of mass m starts from rest at the top of a slope of length D inclined at q above horizontal. She does not push with her poles. Determine the speed of the skier at the bottom of the slope (v) as a function of the appropriate coefficient of friction between the skies and the snow, D, m, q , and g.
| Free-Body Diagram
| Mathematical Analysis
Event 1:
KE1 = GE1 = W12 = |
Event 2:
KE2 = GE2 =
|
Questions
If g = 0 m/s2, what should v equal? Does your function agree with this observation?
If q = 0°, what should v equal? Does your function agree with this observation?
If the D is doubled, what will happen to v?
The driver of an automobile of mass m, traveling down an incline of angle q, suddenly sees an obstacle blocking her lane. Ignoring her reaction time, determine the time elapsed (T) before the car skids to a stop as a function of the initial velocity (v), the appropriate coefficient of friction between the tires and the road, m, q, and g.
| Free-Body Diagram
| Mathematical Analysis
Event 1:
P1x = P1y = J12x = J12y =
|
Event 2:
P2x = P2y =
|
Questions
If m = 0, what should T equal? Does your function agree with this observation?
If m is doubled, what will happen to T?
If v is doubled, what will happen to T?
Is there a maximum angle above which the car will not stop? If so, determine an expression for this angle.
The driver of an automobile of mass m, traveling down an incline of angle q, suddenly sees an obstacle blocking her lane. Ignoring her reaction time, determine the distance (D) the car skids before stopping as a function of the initial velocity (v), the appropriate coefficient of friction between the tires and the road, m, q, and g.
| Free-Body Diagram
| Mathematical Analysis
Event 1:
KE1 = GE1 = W12 = |
Event 2:
KE2 = GE2 =
|
Questions
If m = 0, what should D equal? Does your function agree with this observation?
If m is doubled, what will happen to D?
If v is doubled, what will happen to D?
Is there a maximum angle above which the car will not stop? If so, determine an expression for this angle.
| The device at right guarantees all the excitement of skiing without the need for hills. A skier of mass m begins from rest a distance D from the brick wall. Determine the speed of the skier as he crashes into the wall (v) as a function of the appropriate coefficient of friction between the skies and the snow, the mass of the block (M), D, m, and g.
| 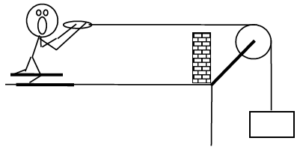 |
Free-Body Diagrams Mathematical Analysis
| skier | block
| Event 1:
Object: KE1 = GE1 = W12 =
Object: KE1 = GE1 = W12 = | Event 2:
KE2 = GE2 =
KE2 = GE2 =
|
Questions
If M = 0, what should v equal? Does your function agree with this observation?
If D is doubled, what will happen to v?
What is the minimum block mass needed for the skier to move?
Two identical automobiles, one moving east at vE and the other moving north at vN, collide. After the collision they remain joined together and move with a common velocity. Determine the angle at which the wreckage skids ( q), measured counterclockwise from east, as a function of vE and vN.
Free-Body Diagrams Mathematical Analysis
| Event 1:
Object: P1x = P1y = J12x = J12y =
Object: P1x = P1y = J12x = J12y =
| Event 2:
P2x = P2y =
P2x = P2y =
|
Questions
If vE = ∞, what should q equal? Does your function agree with this observation?
If vE = vN, what should q equal? Does your function agree with this observation?
[i] a. r2 = 2.23 m b. t2 = 1.49 s
[ii] a. v2 = 2.52 m/s b. r2 = 3.78 m
[iii] m = 51.4 kg
[iv] a. r2 = 14 m b. t2 = 1.75 s
[v] v2 = 27 m/s
[vi] m = 0.14
[vii] v2 = 14.9 m/s
[viii] v2 = 8.89 m/s
[ix] v2 = 14.3 m/s
[x] q = 56°
[xi] v2 = 5.8 m/s
[xii] v2audi = 12.8 m/s
[xiii] v2audi = 4.86 m/s
Homework 6 – Model 2: 110, 111, 112, 113, 114, 127, 129, 130, 132, 139.
- University Physics I Homework Assignments. Authored by: Mary Mohr. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike