6.3: Examples

Law of Conservation of Angular Momentum

The angular momentum of a system of particles around a point in a fixed inertial reference frame is conserved if there is no net external torque around that point:

\[\frac{d \vec{L}}{dt} = 0 \label{11.10}\]

or

\[\vec{L} = \vec{l}_{1} + \vec{l}_{2} + \cdots + \vec{l}_{N} = constant \ldotp \label{11.11}\]

Whiteboard Problem \(\PageIndex{1}\): Space Rescue

The crew of a spaceship has come across an abandoned circular probe, and they want to grab onto it with their tractor beam. The problem is that the crew doesn't know what will happen to them if they do this, because the probe is spinning, at a rate of once every 2 seconds. In this problem, model the spacecraft as being a point of mass 10,000 kg, and the probe as a hollow sphere radius 10 m and a similar mass of 10,000 kg.

1. Assume that turning on the tractor beam to grab the probe has the same effect as attaching the two ships with a massless rigid rod. Describe what would happen to the ships when the tractor beam is turned on.
2. If they are separated by a distance of 100 m when they do this, calculate the final linear speed of the spaceship.

 

Whiteboard Problem \(\PageIndex{2}\): Spinning Platform

I am standing on a frictionless platform holding a spinning bicycle wheel. I'm holding the bicycle wheel so that the axis of rotation is vertical. 

1. As I turn the axis of rotation of the bicycle wheel, I start to spin on the platform. Why?
2. What is the moment of inertia of the wheel, relative to the axis passing through it's center? It has a mass of 4.1 kg and radius 32 cm.
3. Estimate the moment of inertia of my body as I spin on the platform, relative to the vertical axis passing through the center of the platform.
4. Notice that the wheel can spin around it's own axis and around the axis going through the center of the platform. What is the moment of inertia of the center of mass of the wheel as it spins around the axis of the platform? (You will have to estimate how far away from the center I am holding it).
5. Initially, the wheel spins 3 times a second and I am at rest on the platform. Then, I turn the wheel completely around, so my left hand is where my right hand used to be. How fast am I spinning on the platform?

Whiteboard Problem \(\PageIndex{3}\): MY FAVORITE PROBLEM

A ``pulsar'' is a celestial object which ``blinks'' on and off very quickly (in radio wavelengths). I propose that such objects are formed when rotating stars collapse without losing any mass, and since they conserve angular momentum, they are left spinning very quickly. I propose that the blinking is caused by a single hot spot on their surface, so it appears to blink as the pulsar spins. (General Hint: This problem is easier if you use scientific notation for the large numbers, and/or use symbols for as much of it as you can!)

1. What would the radius of a pulsar be if it's a solid sphere, blinking once a second, and formed from the collaspe of the Sun? The Sun rotates at about 15\(^\circ\)/day, and has a radius of 696,000 km.
2. The fastest pulsar (PSR J1748-2442ad, discovered in 2005) spins at 716 times a second. What is the radius of this object, if it formed from a star with the mass of the Sun by my collapse theory?
3. What is the density of this object? Does this density sound reasonable? (maybe Google the density of some objects you know...) You will need the mass of the Sun for this part, 1.99\(\times 10^{30}\) kg.

 

Whiteboard Problem \(\PageIndex{4}\): Calcy Centrifuge

A particular centrifuge has an angular speed that depends on time like
\[\omega(t)=-C\exp ^{-(t-t_0)}+\omega_0,\]
where \(t_0\) and \(\omega_0\) are parameters that can be set by the user, and the constant \(C=1.0\) rad/s. The radius of this centrifuge is 15.5 cm.

1. If we want our centrifuge to start at \(\omega=0\) when \(t=0\) and travel at a maximum angular speed of 105 rad/s as \(t\rightarrow \infty\), what do the constants \(t_0\) and \(\omega_0\) have to be?
2. Draw a sketch of the function \(\omega(t)\).
3. What is the torque as a function of time, \(\tau(t)\), that the motor must act on this centrifuge with? Treat the centrifuge as a solid disk of mass 200 g.
4. Draw a sketch of the function \(\tau(t)\).

Whiteboard Problem \(\PageIndex{5}\): Angular DJ

                                                                

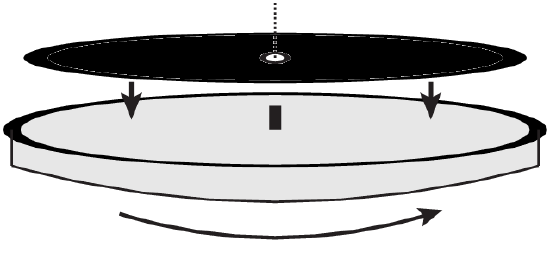
The figure shows a record being dropped onto a turntable. The turntable is initially spinning freely at 0.5 rev/s, and can be modeled as a disk with radius 20 cm, mass 0.50 kg, and moment of inertia \(I=\frac{1}{2}MR^2\).

1. What is the angular speed of the turntable and the record together, after the record is dropped with zero initial angular speed? The record is also a disk, with a radius of 18 cm and mass of 100 g. Note: turntables generally have a motor to keep them spinning at the same rate, but this one is spinning freely and does not!
2. The turntable and record can be stopped by applying a brake to the turntable. This brake applies a small torque of 0.03 Nm. How long does it take this brake to slow the turntable to a stop?

Whiteboard Problems \(\PageIndex{6}\): A Real Life Skater

A figure skater is spinning at 2 rev/s with their arms held out from their body. The mass of this figure skater is 65 kg, and you can assume their body has a moment of inertia of \(I=\frac{1}{4}MR^2\), where \(R\) is the length of their arms. Quick reality check: most of this figure skater's mass is near the center of the rotational axis, so that's why their moment of inertia is less than that of a disk!

1. If their arms are extended to a radius of 50 cm while they are spinning, how big is their moment of inertia?
2. Now they pull their arms in to a distance of 30 cm. How fast are they rotating now, assuming there is no friction between their skates and the ice?
3. Now repeat part (b), assuming friction is acting on their skates with a torque 10.0 Nm. If it takes 3 seconds for them to pull their arms in, how fast will they be rotating after they do so?

Example \(\PageIndex{7}\): Coupled Flywheels

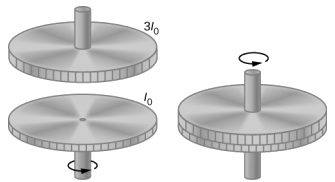
A flywheel rotates without friction at an angular velocity \(\omega_{0}\) = 600 rev/min on a frictionless, vertical shaft of negligible rotational inertia. A second flywheel, which is at rest and has a moment of inertia three times that of the rotating flywheel, is dropped onto it (Figure \(\PageIndex{3}\)). Because friction exists between the surfaces, the flywheels very quickly reach the same rotational velocity, after which they spin together.

1. Use the law of conservation of angular momentum to determine the angular velocity \(\omega\) of the combination.
2. What fraction of the initial kinetic energy is lost in the coupling of the flywheels?

Figure \(\PageIndex{3}\): Two flywheels are coupled and rotate together.

Strategy

Part (a) is straightforward to solve for the angular velocity of the coupled system. We use the result of (a) to compare the initial and final kinetic energies of the system in part (b).

Solution

1. No external torques act on the system. The force due to friction produces an internal torque, which does not affect the angular momentum of the system. Therefore conservation of angular momentum gives \[I_{0} \omega_{0} = (I_{0} + 3I_{0}) \omega, \nonumber\] \[\omega = \frac{1}{4} \omega_{0} = 150\; rev/min = 15.7\; rad/s \ldotp \nonumber\]
2. Before contact, only one flywheel is rotating. The rotational kinetic energy of this flywheel is the initial rotational kinetic energy of the system, \(\frac{1}{2} I_{0} \omega_{0}^{2}\). The final kinetic energy is \[\frac{1}{2} (4I_{0}) \omega^{2} = \frac{1}{2} (4I_{0}) \left(\dfrac{\omega_{0}}{4}\right)^{2} = \frac{1}{8} I_{0} \omega_{0}^{2}. \nonumber\] Therefore, the ratio of the final kinetic energy to the initial kinetic energy is \[\frac{\frac{1}{8} I_{0} \omega_{0}^{2}}{\frac{1}{2} I_{0} \omega_{0}^{2}} = \frac{1}{4} \ldotp \nonumber\] Thus, 3/4 of the initial kinetic energy is lost to the coupling of the two flywheels.

Significance

Since the rotational inertia of the system increased, the angular velocity decreased, as expected from the law of conservation of angular momentum. In this example, we see that the final kinetic energy of the system has decreased, as energy is lost to the coupling of the flywheels. Compare this to the example of the skater in Figure \(\PageIndex{1}\) doing work to bring her arms inward and adding rotational kinetic energy.

Exercise \(\PageIndex{8}\)

A merry-go-round at a playground is rotating at 4.0 rev/min. Three children jump on and increase the moment of inertia of the merry-go-round/children rotating system by 25%. What is the new rotation rate?

Example \(\PageIndex{9}\): Dismount from a High Bar

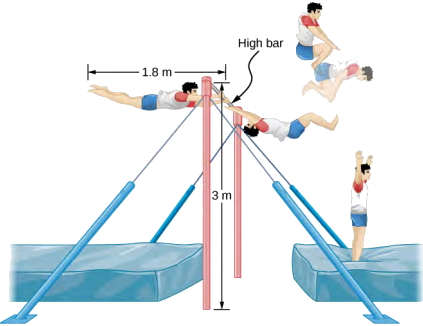
An 80.0-kg gymnast dismounts from a high bar. He starts the dismount at full extension, then tucks to complete a number of revolutions before landing. His moment of inertia when fully extended can be approximated as a rod of length 1.8 m and when in the tuck a rod of half that length. If his rotation rate at full extension is 1.0 rev/s and he enters the tuck when his center of mass is at 3.0 m height moving horizontally to the floor, how many revolutions can he execute if he comes out of the tuck at 1.8 m height? See Figure \(\PageIndex{4}\).

Figure \(\PageIndex{4}\): A gymnast dismounts from a high bar and executes a number of revolutions in the tucked position before landing upright.

Strategy

Using conservation of angular momentum, we can find his rotation rate when in the tuck. Using the equations of kinematics, we can find the time interval from a height of 3.0 m to 1.8 m. Since he is moving horizontally with respect to the ground, the equations of free fall simplify. This will allow the number of revolutions that can be executed to be calculated. Since we are using a ratio, we can keep the units as rev/s and don’t need to convert to radians/s.

Solution

The moment of inertia at full extension is \[I_{0} = \frac{1}{12} mL^{2} = \frac{1}{12} (80.0\; kg)(1.8\; m)^{2} = 21.6\; kg\; \cdotp m^{2} \ldotp \nonumber\]

The moment of inertia in the tuck is \[I_{f} = \frac{1}{12} mL_{f}^{2} = \frac{1}{12} (80.0\; kg)(0.9\; m)^{2} = 5.4\; kg\; \cdotp m^{2} \ldotp \nonumber\]

Conservation of angular momentum: \[I_{f} \omega_{f} = I_{0} \omega_{0} \Rightarrow \omega_{f} = \frac{I_{0} \omega_{0}}{I_{f}} = \frac{(21.6\; kg\; \cdotp m^{2})(1.0\; rev/s)}{5.4\; kg\; \cdotp m^{2}} = 4.0\; rev/s \ldotp \nonumber\]

Time interval in the tuck: \[t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2(3.0 - 1.8) m}{9.8\; m/s}} = 0.5\; s \ldotp \nonumber\]

In 0.5 s, he will be able to execute two revolutions at 4.0 rev/s.

Significance

Note that the number of revolutions he can complete will depend on how long he is in the air. In the problem, he is exiting the high bar horizontally to the ground. He could also exit at an angle with respect to the ground, giving him more or less time in the air depending on the angle, positive or negative, with respect to the ground. Gymnasts must take this into account when they are executing their dismounts.

Example \(\PageIndex{10}\): Conservation of Angular Momentum of a Collision

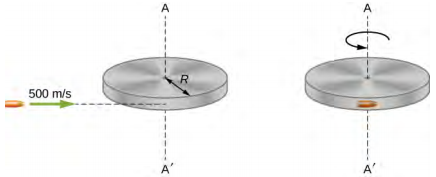
A bullet of mass m = 2.0 g is moving horizontally with a speed of 500.0 m/s. The bullet strikes and becomes embedded in the edge of a solid disk of mass M = 3.2 kg and radius R = 0.5 m. The cylinder is free to rotate around its axis and is initially at rest (Figure \(\PageIndex{5}\)). What is the angular velocity of the disk immediately after the bullet is embedded?

Figure \(\PageIndex{5}\): A bullet is fired horizontally and becomes embedded in the edge of a disk that is free to rotate about its vertical axis.

Strategy

For the system of the bullet and the cylinder, no external torque acts along the vertical axis through the center of the disk. Thus, the angular momentum along this axis is conserved. The initial angular momentum of the bullet is mvR, which is taken about the rotational axis of the disk the moment before the collision. The initial angular momentum of the cylinder is zero. Thus, the net angular momentum of the system is mvR. Since angular momentum is conserved, the initial angular momentum of the system is equal to the angular momentum of the bullet embedded in the disk immediately after impact.

Solution

The initial angular momentum of the system is

\[L_{i} = mvR \ldotp \nonumber\]

The moment of inertia of the system with the bullet embedded in the disk is

\[I = mR^{2} + \frac{1}{2} MR^{2} = \left(m + \dfrac{M}{2}\right) R^{2} \ldotp \nonumber\]

The final angular momentum of the system is

\[L_{f} = I \omega_{f} \ldotp \nonumber\]

Thus, by conservation of angular momentum, L_i = L_f and

\[mvR = \left(m + \dfrac{M}{2}\right) R^{2} \omega_{f} \ldotp \nonumber\]

Solving for \(\omega_{f}\),

\[\omega_{f} = \frac{mvR}{\left(m + \dfrac{M}{2}\right) R^{2}} = \frac{(2.0 \times 10^{-3}\; kg)(500.0\; m/s)}{(2.0 \times 10^{-3}\; kg + 1.6\; kg)(0.50\; m)} = 1.2\; rad/s \ldotp \nonumber\]

Significance

The system is composed of both a point particle and a rigid body. Care must be taken when formulating the angular momentum before and after the collision. Just before impact the angular momentum of the bullet is taken about the rotational axis of the disk.