9.4: Advanced Application- Springs and Collisions

Two Carts Colliding and Compressing a Spring

Unlike the discussion in the previous section, which considered a stationary spring and asked only questions about initial and final states, this example is intended to show you how one can use “energy methods” to solve for the actual motion of a relatively complicated system as a function of time. The system is the two carts colliding, one of them fitted with a spring, considered in Section 9.3. Although all the physics involved is straightforward, the math is at a higher level than you will be using this semester, so I’m presenting this here as a “curiosity” only.

First, recall the total kinetic energy for a collision problem can be written as \(K = K_{cm} + K_{conv}\), where (if the system is isolated) \(K_{cm}\) remains constant throughout. Then, the total mechanical energy \(E = K + U = K_{cm} + K_{conv} + U\). This is also constant, and before the interaction happens, when \(U\) = 0, we have \(E = K_{cm} + K_{conv,i}\), so setting these two things equal and canceling out \(K_{cm}\) we get

\[ K_{\text {conv}}=K_{\text {conv}, i}-U \label{eq:5.15} \]

where the potential energy function is given by Equation (9.2.2). Introducing the relative coordinate \(x_{12} = x_2 − x_1\), and the relative velocity \(v_{12}\), Equation (\ref{eq:5.15}) becomes

\[ \frac{1}{2} \mu v_{12}^{2}=\frac{1}{2} \mu v_{12, i}^{2}-\frac{1}{2} k\left(x_{12}-x_{0}\right)^{2} \label{eq:5.16} \]

an equation that must hold while the interaction is going on. We can solve this for \(v_{12}\), and then notice that both \(x_{12}\) and \(v_{12}\) are functions of time, and the latter is the derivative with respect to time of the former, so

\[ v_{12}=\pm \sqrt{v_{12, i}^{2}-(k / \mu)\left(x_{12}-x_{0}\right)^{2}} \label{eq:5.17} \]

\[ \frac{d x_{12}}{d t}=\pm \sqrt{v_{12, i}^{2}-(k / \mu)\left(x_{12}(t)-x_{0}\right)^{2}} \label{eq:5.18} .\]

(The “\(\pm\)” sign means that the quantity on the right-hand side has to be negative at first, when the carts are coming together, and positive later, when they are coming apart. This is because I have assumed cart 1 starts to the left of cart 2, so going in cart 2, as seen from cart 1, appears to be moving to the left.)

Equation (\ref{eq:5.18}) is what is known, in calculus, as a differential equation. The problem is to find a function of \(t\), \(x_{12}(t)\), such that when you take its derivative you get the expression on the right-hand side. If you know how to calculate derivatives, you can check that the solution is in fact

\[ x_{12}(t)=x_{0}-\frac{v_{12, i}}{\omega} \sin \left[\omega\left(t-t_{c}\right)\right] \quad \text { for } t_{c} \leq t \leq t_{c}+\pi / \omega \label{eq:5.19} \]

where the quantity \(\omega = \sqrt{k/ \mu}\), and the time \(t_c\) is the time cart 1 first makes contact with the spring: \(t_c = (x_{2i} −x_0 −x_{1i})/v_{1i}\). The solution (\ref{eq:5.19}) is valid for as long as the spring is compressed, which is to say, for as long as \(x_{12}(t) < x_0\), or \( \sin \left[\omega\left(t-t_{c}\right)\right]>0 \), which translates to the condition on \(t\) shown above.

Having a solution for \(x_{12}\), we could now obtain explicit results for \(x_1(t)\) and \(x_2(t)\) separately, using the fact that \(x_1 = x_{cm} −m_2x_{12}/(m_1+m_2)\), and \(x_2 = x_{cm} +m_1x_{12}/(m_1 +m_2)\) (compare Eqs. (4.2.1), in chapter 4), and finding the position of the center of mass as a function of time is a trivial problem, since it just moves with constant velocity.

We do not, however, need to do any of this in order to generate the plots of the kinetic and potential energy shown in Figure 8.2.1: the potential energy depends only on \(x_2 − x_1\), which is given explicitly by Equation (\ref{eq:5.19}), and the kinetic energy is equal to \(K_{cm} + K_{conv}\), where \(K_{cm}\) is constant and \(K_{conv}\) is given by Equation (\ref{eq:5.16}), which can also be easily rewritten in terms of Equation (\ref{eq:5.19}). The results are Eqs. (9.2.3) in the text.

Getting the Potential Energy Function from Collision Data

Consider the collision illustrated in Figure 4.3.1. Can we tell what the potential energy function is for the interaction between the two carts?

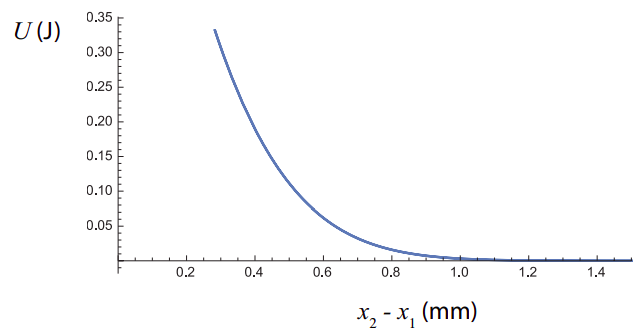
At first sight, it may seem that all the information necessary to “reconstruct” the function \(U(x_1−x_2)\) is available already, at least in graphical form: From Figure 4.3.1 you could get the value of \(x_2 − x_1\) at any time \(t\); then from Figure 8.5.1 you can get the value of \(K\) (in the elastic-collision scenario) for the same value of \(t\); and then you could plot \(U = E − K\) (where \(E\) is the total energy) as a function of \(x_2 − x_1\).

But there is a catch: Figure 4.3.1 shows that the colliding objects never get any closer than \(x_2−x_1\) ≃ 0.28 mm, so we have no way to tell what \(U(x_2−x_1)\) is for smaller values of \(x_2−x_1\). This is essentially the problem faced by particle physicists when they use collisions (which they do regularly) to try to determine the precise nature of the interactions between the particles they study!

You can check this for yourself. The functions I used for \(x_1(t)\) and \(x_2(t)\) in Figure 4.3.1 are

\begin{align}
&x_{1}(t)=\frac{1}{3}\left((2 t-10) \operatorname{erf}(10-2 t)+10 \operatorname{erf}(10)+t-\frac{e^{-4(t-5)^{2}}}{\sqrt{\pi}}\right)-5 \nonumber \\
&x_{2}(t)=\frac{1}{3}\left((5-t) \operatorname{erf}(10-2 t)-5 \operatorname{erf}(10)+t+\frac{e^{-4(t-5)^{2}}}{2 \sqrt{\pi}}\right) \label{eq:5.20}
\end{align}

Here, “erf” is the so-called “error function,” which you can find in any decent library of mathematical functions. This looks complicated, but it just gives you the shapes you want for the velocity curves. The derivative of the above is

\begin{align}
&v_{1}(t)=\frac{1}{3}(1+2 \operatorname{erf}(10-2 t)) \nonumber \\
&v_{2}(t)=\frac{1}{3}(1-\operatorname{erf}(10-2 t)) \label{eq:5.21}
\end{align}

and you may want to try plotting these for yourself; the result should be Figure 4.3.1.

Now, assume (as I did for Figure 8.5.1) that \(m_1\) = 1 kg, and \(m_2\) = 2 kg, and use these values and the results of Eq (\ref{eq:5.21}) (assumed to be in m/s) to calculate \(K_{sys}\) as a function of \(t\). Then \(U = E_{sys} − K_{sys}\), with \(E_{sys}\) = 1/2 J:

\[ U=\frac{1}{2}-\frac{1}{2} m_{1} v_{1}^{2}(t)-\frac{1}{2} m_{2} v_{2}^{2}(t)=\frac{1}{3}\left(1-\operatorname{erf}^{2}(10-2 t)\right) \label{eq:5.22} \]

and now do a parametric plot of \(U\) versus \(x_2 − x_1\), using \(t\) as a parameter. You will end up with a figure like the one below:

Figure \(\PageIndex{1}\). No information can be gathered from those figures (nor from the explicit expressions (\ref{eq:5.20}) and (\ref{eq:5.21}) above) on the values of \(U\) for \(x_2 − x_1\) < 0.28 mm, the distance of closest approach of the two carts.