4.2: "Convertible" and "Translational" Kinetic Energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
Figure 4.2.1 shows how the total kinetic energy varies with time, for the two objects shown colliding in Figure 4.1.1 , depending on the details of the collision, namely, on the value of e. The three curves shown cover the elastic case, e = 1 (Figure 4.1.1), the totally inelastic case, e = 0 (Figure 4.3), and the inelastic case with e = 0.6 of Figure 4.1.4. Recall that the total momentum is conserved in all three cases.
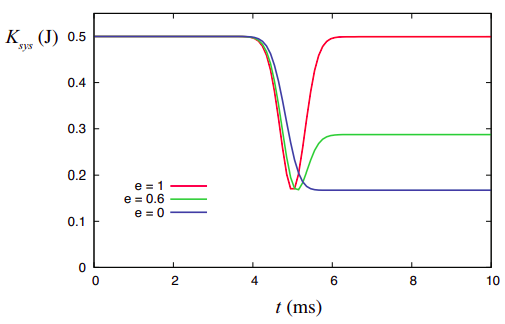
Figure 4.2.1 shows that the greatest loss of kinetic energy happens for the totally inelastic collision, which, as we will see in a moment, is, in fact, a general result. That being the case, the figure also shows that it may not be always be possible to bring the total kinetic energy down to zero, even temporarily. The reason for this is that, if momentum is conserved, the velocity of the center of mass cannot change, so if the center of mass was moving before the collision, it must still be moving afterwards; and, as mentioned in this chapter’s introduction, as long as there is motion in a system, its total kinetic energy cannot be zero.
All of this suggests that it should be possible to break up a system’s total kinetic energy into two parts: one part associated with the motion of the center of mass, which cannot change in any momentum-conserving collision, and one part associated with the relative motion of the parts that make up the system. This second part would vanish irreversibly in a totally inelastic collision, whereas it would recover its original value in an elastic collision.
The way to see this mathematically, for a system of two objects with masses m1 and m2, is to introduce the center of mass velocity vcm [Equation (3.3.3)]
vcm=m1v1+m2v2m1+m2
and the relative velocity v12=v2−v1 (Equation (4.1.3) above), and observe that the velocities v1 and v2 can be written, respectively, as
v1=vcm−m2m1+m2v12v2=vcm+m1m1+m2v12.
Substituting the equations (4.2.2) into the expression Ksys=12m1v21+12m2v22, one finds that the cross-terms vanish, and all that is left is
Ksys=12(m1+m2)v2cm+12m1m22+m2m21(m1+m2)2v212.
A factor of (m1+m2) may be canceled in the last term, and the final expression takes the form
where the center of mass kinetic energy (or translational energy) is just what one would have if the whole system was a single particle of mass M=m1+m2 moving at the center of mass speed:
Kcm=12Mv2cm
and the “convertible energy” Kconv is the part associated with the relative motion, which can be made to vanish entirely in an inelastic collision3:
Kconv=12m1m2m1+m2v212=12μv212.
The last equation implicitly defines a useful quantity that we call the reduced mass of a system of two particles, and denote by µ:
μ=m1m2m1+m2.
Equation (???), with the definitions (???) and (???), pretty much explains everything that we see going on in Figure 4.2.1. The total kinetic energy is the sum of two terms, the first of which, Kcm, can never change: it is, in fact, as constant as the total momentum itself, since it involves the center of mass velocity, vcm, which is proportional to the total momentum of the system (recall equation (3.3.4)). The term that can, and does change, is the second one, the convertible energy. In fact, in an ordinary collision in which the objects do not pass through each other, there must be at least an instant in time when Kconv = 0. This is because it involves the relative velocity, and since the relative velocity must change sign at some point (the objects are initially coming together, but end up moving apart), it must be zero at that time.
This explains why all the curves in Figure 4.2.1 have the same minimum value (even though they may reach it at different times): that value is clearly Kcm for the system (since Kconv is zero at that time). It is the same for all the curves because all the systems considered have the same total mass and momentum (as determined by the initial velocities)—we just chose them that way.
Since Kcm cannot change for an isolated system, the maximum kinetic energy that can be lost in a collision in such a system is the initial value of Kconv, which we would denote as Kconv,i. This is, in fact, completely lost in a totally inelastic collision, since in that case v12,f = 0, and Equation (???) then gives Kconv,f = 0. In fact, using Equation (4.1.9), we can relate the final value of the convertible energy to its initial value via the coefficient of restitution:
Kconv,f=12μv212,f=12μe2v212,i=e2Kconv,i.
Thus, for example, in a collision with e = 0.6, the final value of the convertible energy would be only 0.36 times its initial value: 64% of it would have been “lost.” (This is not, however, the same as 64% of the total initial energy, since the latter still includes Kcm, which does not change.) We can also write Equation (???) as
ΔKsys=(e2−1)Kconv,i=(e2−1)12μv212,i
since the only possible change in Ksys must come from the convertible energy.
Although we have derived the decomposition (???) for the very restricted situation of two objects moving in one dimension, the basic result is quite general: first, everything in the derivation works if v1 and v2 are replaced by vectors →v1 and →v2, so the results holds in three dimensions as well. Second, for a system of any number of particles, one still can write Ksys as Kcm+ another term that depends only on the relative motion of all the pairs of particles. This “generalized convertible energy,” or kinetic energy of relative motion would have the form
Krel=12μ12v212+12μ13v213+…+12μ23v223+…
(in this expression, something like μ23 means a reduced mass like the one in Equation (???), only for masses m2 and m3, and so forth).
When we get to the study of rotational motion, for instance, we will see that the total kinetic energy of an extended rigid object can be written as Kcm+Krot, where Krot, the rotational kinetic energy, is just the same kind of thing as what we have called the “convertible energy” here.
All of the above still leaves unanswered the question of what happens to the convertible energy that is lost in an inelastic collision. Just what is it that it gets converted into? The answer to this question will be the subject of the following chapter.
3Although the name “convertible energy” makes sense in this context, it is not, as far as I can tell, in general usage. I have borrowed it from Mazur’s The Principles and Practice of Physics, but you should probably not expect to find it in other textbooks.
Kinetic Energy and Momentum in Different Reference Frames
I have pointed out repeatedly before that all motion is relative, and so, to some extent, kinetic energy and momentum must be somewhat relative as well. A car in a freight train has a lot of momentum relative to an observer on the ground, but its momentum relative to another car on the same train is zero, since they are not moving relative to each other. The same could be said about its kinetic energy.
In general, if you have a system with a total momentum →psys and inertia M, its center of mass will have a velocity →vcm=→psys/M. Then, if you were to move alongside the system with a velocity exactly equal to →vcm, the total momentum of the system relative to you would be zero. If the system was a solid object, it would not “hit” you if you made contact; there would be no collision. It may help here to think, for instance, of aircraft refueling in flight: if the two planes’ velocities are exactly matched, they can make contact without any damage, just as if they were at rest. A reference frame moving at a system’s center of mass velocity is, for this reason, called a zero-momentum frame for the system in question.
Clearly, in such a reference frame, the translational kinetic energy of the system, Kcm=12Mv2cm, will also be zero (since, in that frame, the center of mass is not moving at all). However, the relative motion term, Kconv, would be completely unaffected by the change in reference frame. This is because, as you may have noticed by now, to convert velocities from one frame of reference to another we just add or subtract from all the velocities the relative velocity of the two frames. This operation, however, will not change any of the relative velocities of the parts of the system, since these are all differences to begin with. Mathematically
(v2+v′)−(v1+v′)=v2−v1
regardless of the value of v′.
So there something we might call absolute (as opposed to “relative”) about the convertible kinetic energy: it is the same, it will have the same value, for any observer, regardless of how fast or in what direction that observer may be moving relative to the system as a whole. We may think of it as an intrinsic (meaning, observer-independent) property of the system.


