21.3: Forces Not Derived From a Potential Energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
As we have seen in the previous section, for interactions that are associated with a potential energy, we are always able to determine the forces from the potential energy by simple differentiation. This means that we do not have to rely exclusively on an equation of the type F=ma, to infer the value of a force from the observed acceleration; rather, we can work in reverse, and predict the value of the acceleration (and from it all the subsequent motion) from our knowledge of the force.
I have said before that, on a microscopic level, all the interactions can be derived from potential energies, yet at the macroscopic level this is not generally true: we have many kinds of interactions for which the associated “stored” or converted energy cannot, in general, be written as a function of the macroscopic position variables for the objects making up the system (by which I mean, typically, the positions of their centers of mass). So what do we do in those cases?
The forces of this type with which we shall deal this semester actually fall into two different categories: the ones that do not dissipate energy, and that we could, in fact, associate with a potential energy if we wanted to3, and the ones that definitely dissipate energy and need special handling. The former category includes the normal force, tension, and the static friction force; the second category includes the force of kinetic (or sliding) friction, and air resistance. A brief description of all these forces, and the methods to deal with them, follows.
3If we wanted to complicate our life, that is...
Tensions
Tension is the force exerted by a stretched spring, and, similarly, by objects such as cables, ropes, and strings in response to a stretching force (or load) applied to them. It is ultimately an elastic force, so, as I said above, we could in principle describe it by a potential energy, but in practice cables, strings and the like are so stiff that it is often all right to neglect their change in length altogether and assume that no potential energy is, in fact, stored in them. The price we pay for this simplification (and it is a simplification) is that we are left without an independent way to determine the value of the tension in any specific case; we just have to infer it from the acceleration of the object on which it acts (since it is a reaction force, it can assume any value as required to adjust to any circumstance—up to the point where the rope snaps, anyway).
Thus, for instance, in the picture below, which shows two blocks connected by a rope over a pulley, the tension force exerted by the rope on block 1 must equal m1a1, where a1 is the acceleration of that block, provided there are no other horizontal forces (such as friction) acting on it. For the hanging block, on the other hand, the net force is the sum of the tension on the other end of the rope (pulling up) and gravity, pulling down. If we choose the upward direction as positive, we can write Newton’s second law for the second block as
Ftr,2−m2g=m2a2.
Two things need to be realized now. First, if the rope is inextensible, both blocks travel the same distance in the same time, so their speeds are always the same, and hence the magnitude of their accelerations will always be the same as well; only the sign may be different depending on which direction we choose as positive. If we take to the right to be positive for the horizontal motion, we will have a2=−a1. I’m just going to call a1=a, so then a2=−a.
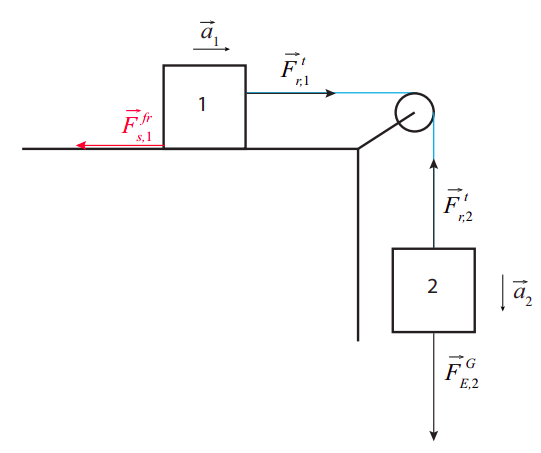
The second thing to note is that, if the rope’s mass is negligible, it will, like an ideal spring, pull with a force with the same magnitude on both ends. With our specific choices (up and to the right is positive), we then have Ftr,2=Ftr,1, and I’m just going to call this quantity Ft . All this yields, then, the following two equations:
Ft=m1aFt−m2g=−m2a.
The system (21.3.2) can be easily solved to get
a=m2gm1+m2Ft=m1m2gm1+m2.
Normal Forces
Normal force is the reaction force with which a surface pushes back when it is being pushed on. Again, this works very much like an extremely stiff spring, this time under compression instead of tension. And, again, we will eschew the potential energy treatment by assuming that the surface’s actual displacement is entirely negligible, and we will just calculate the value of Fn as whatever is needed in order to make Newton’s second law work. Note that this force will always be perpendicular to the surface, by definition (the word “normal” means “perpendicular” here); the task of dealing with a sideways push on the surface will be delegated to the static friction force, to be covered next.
If I am just standing on the floor and not falling through it, the net vertical force acting on me must be zero. The force of gravity on me is mg downwards, and so the upwards normal force must match this value, so for this situation Fn=mg. But don’t get too attached to the notion that the normal force must always be equal to mg, since this will often not be the case. Imagine, for instance, a person standing inside an elevator at the time it is accelerating upwards. With the upwards direction as positive, Newton’s second law for the person reads
Fn−mg=ma
and therefore for this situation
Fn=mg+ma.
If you were weighing yourself on a bathroom scale in the elevator, this is the upwards force that the bathroom scale would have to exert on you, and it would do that by compressing a spring inside, and it would record the “extra” compression (beyond that required by your actual weight, mg) as extra weight. Conversely, if the elevator were accelerating downward, the scale would record you as being lighter. In the extreme case in which the cable of the elevator broke and you, the elevator and the scale ended up (briefly, before the emergency brake caught on) in free fall, you would all be falling with the same acceleration, you would not be pushing down on the scale at all, and its normal force as well as your recorded weight would be zero. This is ultimately the reason for the apparent weightlessness experienced by the astronauts in the space station, where the force of gravity is, in fact, not very much smaller than on the surface of the earth. (We will return to this effect after we have a good grip on two-dimensional, and in particular circular, motion.)
Static and Kinetic Friction Forces
The static friction force is a force that prevents two surfaces in contact from slipping relative to each other. It is an extremely useful force, since we would not be able to drive a car, or ride a bicycle, or even walk, without it—as we know from experience, if we have ever tried to do any of those things on a low-friction surface (such as a sheet of ice).
The science behind friction (known technically as tribology) is actually not very simple at all, and it is of great current interest for many reasons—whether the ultimate goal is to develop ways to reduce friction or to increase it. On an elementary level, we are all aware of the fact that even a surface that looks smooth on a macroscopic scale will actually exhibit irregularities, such as ridges and valleys, under a microscope. It makes sense, then, that when two such surfaces are pressed together, the bumps on one of them will hit, and be held in place by, the bumps on the other one, and that will prevent sliding until and unless a sufficient force is applied to temporarily “flatten” the bumps enough to allow the thing to move4.
As long as this does not happen, that is, as long as the surfaces do not slide relative to each other, we say we are dealing with the static friction force, which is, at least approximately, an elastic force that does not dissipate energy: the small distortion of the “bumps” on the surfaces that takes place when you push on them typically happens slowly enough, and is small enough, to be reversible, so that when you stop pushing the two surfaces just go back to their initial state. This is no longer the case once the surfaces start sliding relative to each other. At that point the character of the friction force changes, and we have to deal with the sliding, or kinetic friction force, as I will explain below.
The static friction force is also, like tension and the normal force, a reaction force that will adjust itself, within limits, to take any value required to prevent slippage in a given circumstance. Hence, its actual value in a particular situation cannot really be ascertained until the other relevant forces— the other forces pushing or pulling on the object—are known.
For instance, for the system in Figure 21.3.1, imagine there is a force of static friction between block 1 and the surface on which it rests, sufficiently large to keep it from sliding altogether. How large does this have to be? If there is no acceleration (a = 0), the equivalent of system (21.3.2) will be
Fss,1+Ft=0Ft−m2g=0
where Fss,1 is the force of static friction exerted by the surface on block 1, and we are going to let the math tell us what sign it is supposed to have. Solving the system (21.3.8) we just get the condition
Fss,1=−m2g
so this is how large Fss,1 has to be in order to keep the whole system from moving in this case.
There is an empirical formula that tells us approximately how large the force of static friction can get in a given situation. The idea behind it is that, microscopically, the surfaces are in contact only near the top of their respective ridges. If you press them together harder, some of the ridges get flattened and the effective contact area increases; this in turn makes the surfaces more resistant to slippage. A direct measure of how strongly the two surfaces press against each other is, actually, just the normal force they exert on each other. So, in general, we expect the maximum force that static friction will be able to exert to be proportional to the normal force between the surfaces:
where s_1 and s_2 just mean “surface 1” and “surface 2,” respectively, and the number \mu_s is known as the coefficient of static friction: it is a tabulated quantity that is determined experimentally, by testing the slippage of different surfaces against each other under different loads.
In our example, the normal force exerted by the surface on block 1 has to be equal to m_1g, since there is no vertical acceleration for that block, and so the maximum value that F^s may have in this case is \mu_sm_1g, whatever \mu_s might happen to be. In fact, this setup would give us a way to determine \mu_s for these two surfaces: start with a small value of m_2, and gradually increase it until the system starts moving. At that point we will know that m_2g has just exceeded the maximum possible value of \left|F^s_{12}\right|, namely, \mu_sm_1g, and so \mu_s = (m_2)_{max}/m_1, where (m_2)_{max} is the largest mass we can hang before the system starts moving.
By contrast with all of the above, the kinetic friction force, which always acts so as to oppose the relative motion of the two surfaces when they are actually slipping, is not elastic, it is definitely dissipative, and, most interestingly, it is also not much of a reactive force, meaning that its value can be approximately predicted for any given circumstance, and does not depend much on things such as how fast the surfaces are actually moving relative to each other. It does depend on how hard the surfaces are pressing against each other, as quantified by the normal force, and on another tabulated quantity known as the coefficient of kinetic friction:
\left|F_{s 1, s 2}^{k}\right|=\mu_{k}\left|F_{s 1, s 2}^{n}\right| \label{eq:6.30}
Note that, unlike for static friction, this is not the maximum possible value of |F^k|, but its actual value; so if we know F^n (and \mu_k) we know F^k without having to solve any other equations (its sign does depend on the direction of motion, of course). The coefficient \mu_k is typically a little smaller than \mu_s, reflecting the fact that once you get something you have been pushing on to move, keeping it in motion with constant velocity usually does not require the same amount of force.
To finish off with our example in Figure \PageIndex{1}, suppose the system is moving, and there is a kinetic friction force F^k_{s,1} between block 1 and the surface. The equations (\ref{eq:6.23}) then have to be changed to
\begin{align} F^{t}-\mu_{k} m_{1} g &=m_{1} a \nonumber \\ F^{t}-m_{2} g &=-m_{2} a \label{eq:6.31} \end{align}
and the solution now is
You may ask, why does kinetic friction dissipate energy? A qualitative answer is that, as the surfaces slide past each other, their small (sometimes microscopic) ridges are constantly “bumping” into each other; so you have lots of microscopic collisions happening all the time, and they cannot all be perfectly elastic. So mechanical energy is being “lost.” In fact, it is primarily being converted to thermal energy, as you can verify experimentally: this is why you rub your hands together to get warm, for instance. More dramatically, this is how some people (those who really know what they are doing!) can actually start a fire by rubbing sticks together.
4This picture based, essentially, on classical physics, leaves out an atomic-scale effect that may be important in some cases, which is the formation of weak bonds between the atoms of both surfaces, resulting in an actual “adhesive” force. This is, for instance, how geckos can run up vertical walls. For our purposes, however, the classical picture (of small ridges and valleys bumping into each other) will suffice to qualitatively understand all the examples we will cover this semester.
Air Resistance
Air resistance is an instance of fluid resistance or drag, a force that opposes the motion of an object through a fluid. Microscopically, you can think of it as being due to the constant collisions of the object with the air molecules, as it cleaves its way through the air. As a result of these collisions, some of its momentum is transferred to the air, as well as some of its kinetic energy, which ends up as thermal energy (as in the case of kinetic friction discussed above). The very high temperatures that air resistance can generate can be seen, in a particularly dramatic way, on the re-entry of spacecraft into the atmosphere.
Unlike kinetic friction between solid surfaces, the fluid drag force does depend on the velocity of the object (relative to the fluid), as well as on a number of other factors having to do with the object’s shape and the fluid’s density and viscosity. Very roughly speaking, for low velocities the drag force is proportional to the object’s speed, whereas for high velocities it is proportional to the square of the speed.
In principle, one can use the appropriate drag formula together with Newton’s second law to calculate the effect of air resistance on a simple object thrown or dropped; in practice, this requires a somewhat more advanced math than we will be using this course, and the formulas themselves are complicated, so I will not introduce them here.
One aspect of air resistance that deserves to be mentioned is what is known as “terminal velocity”. Since air resistance increases with speed, if you drop an object from a sufficiently great height, the upwards drag force on it will increase as it accelerates, until at some point it will become as large as the downward force of gravity. At that point, the net force on the object is zero, so it stops accelerating, and from that point on it continues to fall with constant velocity. When the Greek philosopher Aristotle was trying to figure out the motion of falling bodies, he reasoned that, since air was just another fluid, he could slow down the fall (in order to study it better) without changing the physics by dropping objects in liquids instead of air. The problem with this approach, though, is that terminal velocity is reached much faster in a liquid than in air, so Aristotle missed entirely the early stage of approximately constant acceleration, and concluded (wrongly) that the natural way all objects fell was with constant velocity. It took almost two thousand years until Galileo disproved that notion by coming up with a better method to slow down the falling motion—namely, by using inclined planes.


