21.4: Examples

Problem-Solving Strategy: Work-Energy Theorem

1. Draw a free-body diagram for each force on the object.
2. Determine whether or not each force does work over the displacement in the diagram. Be sure to keep any positive or negative signs in the work done.
3. Add up the total amount of work done by each force.
4. Set this total work equal to the change in kinetic energy and solve for any unknown parameter.
5. Check your answers. If the object is traveling at a constant speed or zero acceleration, the total work done should be zero and match the change in kinetic energy. If the total work is positive, the object must have sped up or increased kinetic energy. If the total work is negative, the object must have slowed down or decreased kinetic energy

 

Whiteboard Problem \(\PageIndex{1}\): Conservative vs Nonconservative

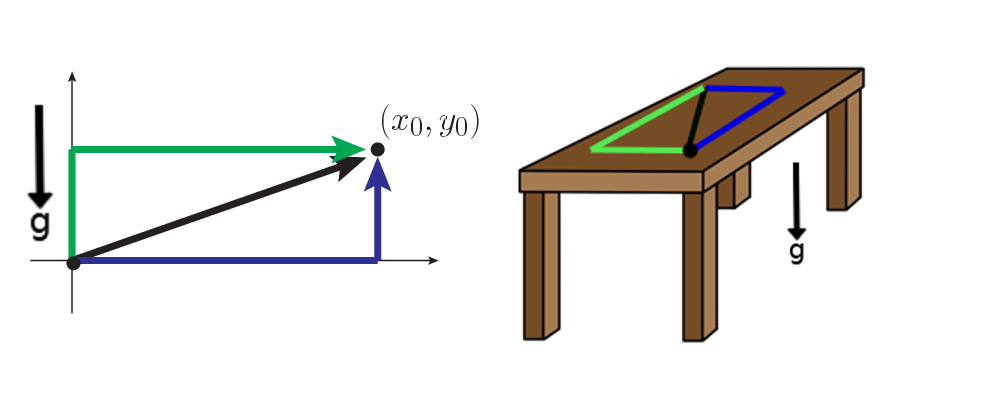
Consider moving an object, of mass \(m\) = 8.75 kg, from the origin to point \((x_0,y_0)=(7.2,3.5)\) m, along three different paths as shown in the figure.

1. First assume the only force acting on the object is gravity, which is directed downwards (so \(\vec{g}=-g\hat{y}\)). Find the work done by the gravitational force on the object for each of the three paths in the figure on the left. 
2. Now consider dragging this object around the surface of a table, as shown in the figure on the right. If the coefficient of friction between the table and the particle is 0.15, find the work done by friction for each path.

 

Whiteboard Problem \(\PageIndex{2}\): Terror on an Elevator

You have been tasked with designing a ``worst-case scenario'' safety system for an elevator. If this 2000-kg elevator's cables break at the top of it's tower, it will be moving with a speed of 25 m/s when it reaches the bottom. Your job is to determine the parameters required if this elevator will be stopped by brakes or a safety spring, over a distance of 3.00 m.

1. Using brakes that apply a constant force, how much force would the brakes have to apply to stop the elevator?
2. Using a spring, what would the spring constant need to be to stop this elevator?
3. What if you used both? If the brakes apply a force of 17 kN, what would the spring constant need to be? 

 

Example \(\PageIndex{3}\): Loop-the-Loop

The frictionless track for a toy car includes a loop-the-loop of radius \(R\). How high, measured from the bottom of the loop, must the car be placed to start from rest on the approaching section of track and go all the way around the loop?

Figure \(\PageIndex{2}\): A frictionless track for a toy car has a loop-the-loop in it. How high must the car start so that it can go around the loop without falling off?

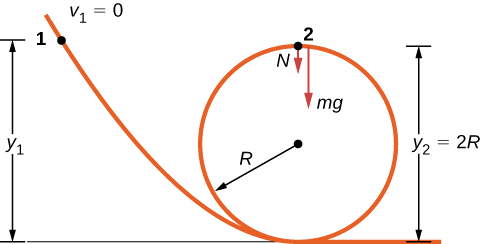
Strategy

The free-body diagram at the final position of the object is drawn in Figure \(\PageIndex{2}\). The gravitational work is the only work done over the displacement that is not zero. Since the weight points in the same direction as the net vertical displacement, the total work done by the gravitational force is positive. From the work-energy theorem, the starting height determines the speed of the car at the top of the loop,

\[mg(y_{2} - y_{1}) = \dfrac{1}{2} mv_{2}^{2}, \nonumber\]

where the notation is shown in the accompanying figure. At the top of the loop, the normal force and gravity are both down and the acceleration is centripetal, so

\[a_{top} = \dfrac{F}{m} = \dfrac{N + mg}{m} = \frac{v_{2}^{2}}{R} \ldotp \nonumber\]

The condition for maintaining contact with the track is that there must be some normal force, however slight; that is, \(N > 0\). Substituting for \(v_{2}^{2}\) and \(N\), we can find the condition for \(y_1\).

Solution

Implement the steps in the strategy to arrive at the desired result:

\[N = -mg + \frac{mv_{2}^{2}}{R} = \frac{-mgR + 2mg(y_{1} - 2R)}{R} > 0\; or\; y_{1} > \frac{5R}{2} \ldotp \nonumber\]

Significance

On the surface of the loop, the normal component of gravity and the normal contact force must provide the centripetal acceleration of the car going around the loop. The tangential component of gravity slows down or speeds up the car. A child would find out how high to start the car by trial and error, but now that you know the work-energy theorem, you can predict the minimum height (as well as other more useful results) from physical principles. By using the work-energy theorem, you did not have to solve a differential equation to determine the height.

Exercise \(\PageIndex{4}\)

Suppose the radius of the loop-the-loop in Example \(\PageIndex{1}\) is 15 cm and the toy car starts from rest at a height of 45 cm above the bottom. What is its speed at the top of the loop?

In situations where the motion of an object is known, but the values of one or more of the forces acting on it are not known, you may be able to use the work-energy theorem to get some information about the forces. Work depends on the force and the distance over which it acts, so the information is provided via their product.

Example \(\PageIndex{5}\): Determining a Stopping Force

A bullet has a mass of 40 grains (2.60 g) and a muzzle velocity of 1100 ft./s (335 m/s). It can penetrate eight 1-inch pine boards, each with thickness 0.75 inches. What is the average stopping force exerted by the wood, as shown in Figure \(\PageIndex{3}\)?

Figure \(\PageIndex{3}\): The boards exert a force to stop the bullet. As a result, the boards do work and the bullet loses kinetic energy

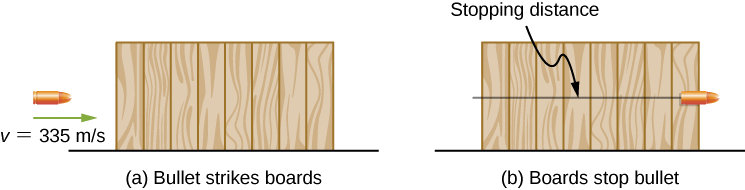
Strategy

We can assume that under the general conditions stated, the bullet loses all its kinetic energy penetrating the boards, so the work-energy theorem says its initial kinetic energy is equal to the average stopping force times the distance penetrated. The change in the bullet’s kinetic energy and the net work done stopping it are both negative, so when you write out the work-energy theorem, with the net work equal to the average force times the stopping distance, that’s what you get. The total thickness of eight 1-inch pine boards that the bullet penetrates is 8 x \(\frac{3}{4}\) in. = 6 in. = 15.2 cm.

Solution

Applying the work-energy theorem, we get

\[W_{net} = - F_{ave} \Delta s_{stop} = - K_{initial} , \nonumber\]

so

\[F_{ave} = \frac{\frac{1}{2} mv^{2}}{\Delta s_{stop}} = \frac{\frac{1}{2} (2.66 \times 10^{-3}\; kg)(335\; m/s)^{2}}{0.152\; m} = 960\; N \ldotp \nonumber\]

Significance

We could have used Newton’s second law and kinematics in this example, but the work-energy theorem also supplies an answer to less simple situations. The penetration of a bullet, fired vertically upward into a block of wood, is discussed in one section of Asif Shakur’s recent article [“Bullet-Block Science Video Puzzle.” The Physics Teacher (January 2015) 53(1): 15-16]. If the bullet is fired dead center into the block, it loses all its kinetic energy and penetrates slightly farther than if fired off-center. The reason is that if the bullet hits off-center, it has a little kinetic energy after it stops penetrating, because the block rotates. The work-energy theorem implies that a smaller change in kinetic energy results in a smaller penetration.

Learn more about work and energy in this PhET simulation (https://phet.colorado.edu/en/simulation/the-ramp) called “the ramp.” Try changing the force pushing the box and the frictional force along the incline. The work and energy plots can be examined to note the total work done and change in kinetic energy of the box.

Example \(\PageIndex{6}\): Work, energy and the choice of system- dissipative case

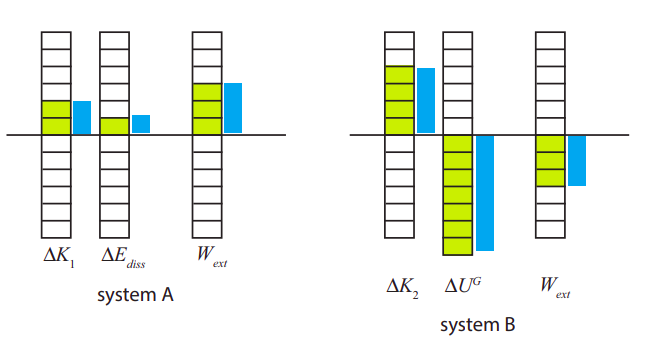
Consider again the situation shown in Figure 21.3.1. Let \(m_1\) = 1 kg, \(m_2\) = 2 kg, and \(\mu_k\) = 0.3. Use the solutions provided in section 21.3 to calculate the work done by all the forces, and the changes in all energies, when the system undergoes a displacement of 0.5 m, and represent the changes graphically using bar diagrams like the ones in Figure 21.2.2 (for system A and B separately)

Solution

From Equation (21.3.11), we have

\begin{align}
a &=\frac{m_{2}-\mu_{k} m_{1}}{m_{1}+m_{2}} g=5.55 \: \frac{\mathrm{m}}{\mathrm{s}^{2}} \nonumber \\
F^{t} &=\frac{m_{1} m_{2}\left(1+\mu_{k}\right)}{m_{1}+m_{2}} g=8.49 \: \mathrm{N} \label{eq:7.34}
\end{align}

We can use the acceleration to calculate the change in kinetic energy, since we have Equation (15.2.10) for motion with constant acceleration:

\[ v_{f}^{2}-v_{i}^{2}=2 a \Delta x=2 \times\left(5.55 \: \frac{\mathrm{m}}{\mathrm{s}^{2}}\right) \times 0.5 \: \mathrm{m}=5.55 \: \frac{\mathrm{m}^{2}}{\mathrm{s}^{2}} \label{eq:7.35} \]

so the change in kinetic energy of the two blocks is

\begin{align}
&\Delta K_{1}=\frac{1}{2} m_{1}\left(v_{f}^{2}-v_{i}^{2}\right)=2.78 \: \mathrm{J} \nonumber \\
&\Delta K_{2}=\frac{1}{2} m_{2}\left(v_{f}^{2}-v_{i}^{2}\right)=5.55 \: \mathrm{J} \label{eq:7.36}.
\end{align}

We can also use the tension to calculate the work done by the external force on each system:

\begin{align}
W_{e x t, A} &=F_{r, 1}^{t} \Delta x=(8.49 \: \mathrm{N}) \times(0.5 \: \mathrm{m})=4.25 \: \mathrm{J} \nonumber \\
W_{e x t, B} &=F_{r, 2}^{t} \Delta y=(8.49 \: \mathrm{N}) \times(-0.5 \: \mathrm{m})=-4.25 \: \mathrm{J} \label{eq:7.37}.
\end{align}

Lastly, we need the change in the gravitational potential energy of system B:

\[ \Delta U_{B}^{G}=m_{2} g \Delta y=(2 \: \mathrm{kg}) \times\left(9.8 \: \frac{\mathrm{m}}{\mathrm{s}^{2}}\right) \times(-0.5 \: \mathrm{m})=-9.8 \: \mathrm{J} \label{eq:7.38} \]

and the increase in dissipated energy in system A, which we can get from Equation (21.2.16):

\[ \Delta E_{\text {diss}}=-F_{s, 1}^{k} \Delta x=\mu_{k} F_{s, 1}^{n} \Delta x=\mu_{k} m_{1} g \Delta x=0.3 \times(1 \: \mathrm{kg}) \times\left(9.8 \: \frac{\mathrm{m}}{\mathrm{s}^{2}}\right) \times(0.5 \: \mathrm{m})=1.47 \: \mathrm{J} \label{eq:7.39} .\]

We can now put all this together to show that Equation (21.2.8) indeed holds:

\begin{align}
W_{e x t, A} &=\Delta E_{A}=\Delta K_{1}+\Delta E_{d i s s}=2.78 \: \mathrm{J}+1.47 \: \mathrm{J}=4.25 \: \mathrm{J} \nonumber \\
W_{e x t, B} &=\Delta E_{B}=\Delta K_{2}+\Delta U_{B}^{G}=5.55 \: \mathrm{J}-9.8 \: \mathrm{J}=-4.25 \: \mathrm{J} \label{eq:7.40} .
\end{align}

To plot all this as energy bars, if you do not have access to a very precise drawing program, you typically have to make some approximations. In this case, we see that \(\Delta K_2 = 2\Delta K_1\) (exactly), whereas \( \Delta K_{1} \simeq 2 \Delta E_{d i s s}\), so we can use one box to represent \(E_{diss}\), two boxes for \(\Delta K_1\), three for \(W_{ext,A}\), four for \(\Delta K_2\), and so on. The result is shown in green in the picture below; the blue bars have been drawn more exactly to scale, and are shown for your information only.

Example \(\PageIndex{7}\): Work, energy and the choice of system- non-dissipative case

Suppose you hang a spring from the ceiling, then attach a block to the end of the spring and let go. The block starts swinging up and down on the spring. Consider the initial time just before you let go, and the final time when the block momentarily stops at the bottom of the swing. For each of the choices of a system listed below, find the net energy change of the system in this process, and relate it explicitly to the work done on the system by an external force (or forces)

1. System is the block and the spring.
2. System is the block alone.
3. System is the block and the earth.

Solution

(a) The block alone has kinetic energy, and the spring alone has (elastic) potential energy, so the total energy of this system is the sum of these two. For the interval considered, the change in kinetic energy is zero, because the block starts and ends (momentarily) at rest, so only the spring energy changes. This has to be equal to the work done by gravity, which is the only external force.

So, if the spring stretches a distance d, its potential energy goes from zero to \(\frac{1}{2}kd^2\), and the block falls the same distance, so gravity does an amount of work equal to \(mgd\), and we have

\[ W_{g r a v}=m g d=\Delta E_{s y s}=\Delta K+\Delta U^{s p r}=0+\frac{1}{2} k d^{2} \label{eq:7.41} .\]

(b) If the system is the block alone, the only energy it has is kinetic energy, which, as stated above, does not see a net change in this process. This means the net work done on the block by the external forces must be zero. The external forces in this case are the spring force and gravity, so we have

\[ W_{s p r}+W_{g r a v}=\Delta K=0 \label{eq:7.42} .\]

We have calculated \(W_{grav}\) above, so from this we get that the work done by the spring on the block, as it stretches, is \(−mgd\), or (by Equation (\ref{eq:7.41})) \(−\frac{1}{2}kd^2\). Note that the force exerted by the spring is not constant as it stretches (or compresses) so we cannot just use Equation (9.2.1) to calculate it; rather, we need to calculate it as an integral, as in Equation (21.2.5), or derive it in some indirect way as we have just done here.

(c) If the system is the block and the earth, it has kinetic energy and gravitational potential energy. The force exerted by the spring is an external force now, so we have:

\[ W_{s p r}=\Delta E_{s y s}=\Delta K+\Delta U^{G}=0-m g d \label{eq:7.43} \]

so we end up again with the result that \(W_{spr} = −mgd = −\frac{1}{2}kd^2\). Note that both the work done by the spring and the work done by gravity are equal to the negative of the changes in their respective potential energies, as they should be.

 

Example \(\PageIndex{8}\): Jumping

For a standing jump, you start standing straight (A) so your body’s center of mass is at a height \(h_1\) above the ground. You then bend your knees so your center of mass is now at a (lower) height \(h_2\) (B). Finally, you straighten your legs, pushing hard on the ground, and take off, so your center of mass ends up achieving a maximum height, \(h_3\), above the ground (C). Answer the following questions in as much detail as you can.

1. Consider the system to be your body only. In going from (A) to (B), which external forces are acting on it? How do their magnitudes compare, as a function of time?
2. In going from (A) to (B), does any of the forces you identified in part (a) do work on your body? If so, which one, and by how much? Does your body’s energy increase or decrease as a result of this? Into what kind of energy do you think this work is primarily converted?
3. In going from (B) to (C), which external forces are acting on you? (Not all of them need to be acting all the time.) How do their magnitudes compare, as a function of time?
4. In going from (B) to (C), does any of the forces you identified do work on your body? If so, which one, and by how much? Does your body’s kinetic energy see a net change from (B) to (C)? What other energy change needs to take place in order for Equation (21.2.8) (always with your body as the system) to be valid for this process?

Solution

(a) The external forces on your body are gravity, pointing down, and the normal force from the floor, pointing up. Initially, as you start lowering your center of mass, the normal force has to be slightly smaller than gravity, since your center of mass acquires a small downward acceleration. However, eventually \(F^n\) would have to exceed \(F^G\) in order to stop the downward motion.

(b) The normal force does no work, because its point of application (the soles of your feet) does not move, so \(\Delta x\) in the expression \(W = F\Delta x\) (Equation (9.2.1)) is zero.

Gravity, on the other hand, does positive work, since you may always treat the center of mass as the point of application of gravity. We have \(F^G_y = −mg\), and \(\Delta y = h_2 − h_1\), so

\[ W_{g r a v}=F_{y}^{G} \Delta y=-m g\left(h_{2}-h_{1}\right)=m g\left(h_{1}-h_{2}\right) \nonumber .\]

Since this is the net work done by all the external forces on my body, and it is positive, the total energy in my body must have increased (by the theorem ((21.2.8)): \(W_{ext,sys} = \Delta E_{sys}\)). In this case, it is clear that the main change has to be an increase in my body’s elastic potential energy, as my muscles tense for the jump. (An increase in thermal energy is always possible too.)

(c) During the jump, the external forces acting on me are again gravity and the normal force, which together determine the acceleration of my center of mass. At the beginning of the jump, the normal force has to be much stronger than gravity, to give me a large upwards acceleration. Since the normal force is a reaction force, I accomplish this by pushing very hard with my feet on the ground, as I extend my leg’s muscles: by Newton’s third law, the ground responds with an equal and opposite force upwards.

As my legs continue to stretch, and move upwards, the force they exert on the ground decreases, and so does \(F^n\), which eventually becomes less than \(F^G\). At that point (probably even before my feet leave the ground) the acceleration of my center of mass becomes negative (that is, pointing down). This ultimately causes my upwards motion to stop, and my body to come down.

(d) The only force that does work on my body during the process described in (c) is gravity, since, again, the point of application of \(F^n\) is the point of contact between my feet and the ground, and that point does not move up or down—it is always level with the ground. So \(W_{ext,sys} = W_{grav}\), which in this case is actually negative: \(W_{grav} = −mg(h_3 − h_2)\).

In going from (B) to (C), there is no change in your kinetic energy, since you start at rest and end (momentarily) with zero velocity at the top of the jump. So the fact that there is a net negative work done on you means that the energy inside your body must have gone down. Clearly, some of this is just a decrease in elastic potential energy. However, since \(h_3\) (the final height of your center of mass) is greater than \(h_1\) (its initial height at (A), before crouching), there is a net loss of energy in your body as a result of the whole process. The most obvious place to look for this loss is in chemical energy: you “burned” some calories in the process, primarily when pushing hard against the ground.

Example \(\PageIndex{9}\): analyzing a car crash

At a stoplight, a large truck (3000 kg) collides with a motionless small car (1200 kg). The truck comes to an instantaneous stop; the car slides straight ahead, coming to a stop after sliding 10 meters. The measured coefficient of friction between the car’s tires and the road was 0.62. How fast was the truck moving at the moment of impact?

Strategy

At first it may seem we don’t have enough information to solve this problem. Although we know the initial speed of the car, we don’t know the speed of the truck (indeed, that’s what we’re asked to find), so we don’t know the initial momentum of the system. Similarly, we know the final speed of the truck, but not the speed of the car immediately after impact. The fact that the car eventually slid to a speed of zero doesn’t help with the final momentum, since an external friction force caused that. Nor can we calculate an impulse, since we don’t know the collision time, or the amount of time the car slid before stopping. A useful strategy is to impose a restriction on the analysis.

Suppose we define a system consisting of just the truck and the car. The momentum of this system isn’t conserved, because of the friction between the car and the road. But if we could find the speed of the car the instant after impact—before friction had any measurable effect on the car—then we could consider the momentum of the system to be conserved, with that restriction.

Can we find the final speed of the car? Yes; we invoke the work-kinetic energy theorem.

Solution

First, define some variables. Let:

• M_c and M_T be the masses of the car and truck, respectively
• v_T,i and v_T,f be the velocities of the truck before and after the collision, respectively
• v_c,i and v_c,f be the velocities of the car before and after the collision, respectively
• K_i and K_f be the kinetic energies of the car immediately after the collision, and after the car has stopped sliding (so K_f = 0).
• d be the distance the car slides after the collision before eventually coming to a stop.

Since we actually want the initial speed of the truck, and since the truck is not part of the work-energy calculation, let’s start with conservation of momentum. For the car + truck system, conservation of momentum reads

\[\begin{split} p_{i} & = p_{f} \\ M_{c} v_{c,i} + M_{T} v_{T,i} & = M_{c} v_{c,f} + M_{T} v_{T,f} \ldotp \end{split}\]

Since the car’s initial velocity was zero, as was the truck’s final velocity, this simplifies to

\[v_{T,i} = \frac{M_{c}}{M_{T}} v_{c,f} \ldotp\]

So now we need the car’s speed immediately after impact. Recall that

\[W = \Delta K\]

where

\[\begin{split} \Delta K & = K_{f} - K_{i} \\ & = 0 - \frac{1}{2} M_{c} v_{c,f}^{2} \ldotp \end{split}\]

Also,

\[W = \vec{F}\; \cdotp \vec{d} = Fd \cos \theta \ldotp\]

The work is done over the distance the car slides, which we’ve called d. Equating:

\[Fd \cos \theta = - \frac{1}{2} M_{c} v_{c,f}^{2} \ldotp\]

Friction is the force on the car that does the work to stop the sliding. With a level road, the friction force is

\[F = \mu_{k} M_{c} g \ldotp\]

Since the angle between the directions of the friction force vector and the displacement d is 180°, and cos(180°) = –1, we have

\[- (\mu_{k} M_{c} g) d = - \frac{1}{2} M_{c} v_{c,f}^{2}\]

(Notice that the car’s mass divides out; evidently the mass of the car doesn’t matter.)

Solving for the car’s speed immediately after the collision gives

\[v_{c,f} = \sqrt{2 \mu_{k} gd} \ldotp\]

Substituting the given numbers:

\[\begin{split} v_{c,f} & = \sqrt{2(0.62)(9.81\; m/s^{2})(10\; m)} \\ & = 11.0\; m/s \ldotp \end{split}\]

Now we can calculate the initial speed of the truck:

\[v_{T,i} = \left(\dfrac{1200\; kg}{3000\; kg}\right) (11.0\; m/s) = 4.4\; m/s \ldotp\]

Significance

This is an example of the type of analysis done by investigators of major car accidents. A great deal of legal and financial consequences depend on an accurate analysis and calculation of momentum and energy.