11.A: Geometric Optics and Image Formation (Answers)
- Last updated
- Jan 13, 2021
- Save as PDF
- Page ID
- 32260
( \newcommand{\kernel}{\mathrm{null}\,}\)
Check Your Understanding
Conceptual Questions
1. Virtual image cannot be projected on a screen. You cannot distinguish a real image from a virtual image simply by judging from the image perceived with your eye.
3. Yes, you can photograph a virtual image. For example, if you photograph your reflection from a plane mirror, you get a photograph of a virtual image. The camera focuses the light that enters its lens to form an image; whether the source of the light is a real object or a reflection from mirror (i.e., a virtual image) does not matter.
5. No, you can see the real image the same way you can see the virtual image. The retina of your eye effectively serves as a screen.
7. The mirror should be half your size and its top edge should be at the level of your eyes. The size does not depend on your distance from the mirror.
9. when the object is at infinity; see the mirror equation
11. Yes, negative magnification simply means that the image is upside down; this does not prevent the image from being larger than the object. For instance, for a concave mirror, if distance to the object is larger than one focal distance but smaller than two focal distances the image will be inverted and magnified.
13. answers may vary
15. The focal length of the lens is fixed, so the image distance changes as a function of object distance.
17. Yes, the focal length will change. The lens maker’s equation shows that the focal length depends on the index of refraction of the medium surrounding the lens. Because the index of refraction of water differs from that of air, the focal length of the lens will change when submerged in water.
19. A relaxed, normal-vision eye will focus parallel rays of light onto the retina.
21. A person with an internal lens will need glasses to read because their muscles cannot distort the lens as they do with biological lenses, so they cannot focus on near objects. To correct nearsightedness, the power of the intraocular lens must be less than that of the removed lens.
23. Microscopes create images of macroscopic size, so geometric optics applies.
25. The eyepiece would be moved slightly farther from the objective so that the image formed by the objective falls just beyond the focal length of the eyepiece.
Problems
27.
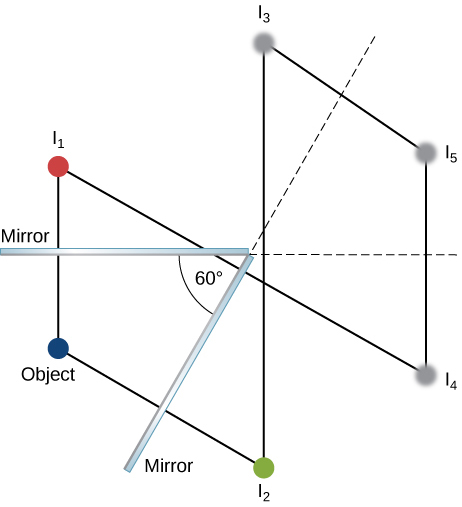
29. It is in the focal point of the big mirror and at the center of curvature of the small mirror.
31. f=R2⇒R=+1.60m
33. do=27.3cm
35. Step 1: Image formation by a mirror is involved.
Step 2: Draw the problem set up when possible.
Step 3: Use thin-lens equations to solve this problem.
Step 4: Find f.
Step 5: Given: m=1.50,do=0.120m.
Step 6: No ray tracing is needed.
Step 7: Using m=dido,di=−0.180m. Then, f=0.360m.
Step 8: The image is virtual because the image distance is negative. The focal length is positive, so the mirror is concave.
37. a. for a convex mirror di<0⇒m>0.m=+0.111;
b. di=−0.334cm (behind the cornea);
c. f=−0.376cm, so that R=−0.752cm
39. m=hiho=−dido=−−dodo=dodo=1⇒hi=ho
41. m=−11.0 A′=0.110m2 I=6.82kW/m2
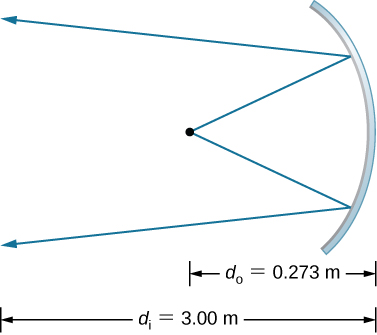
43. x2m=−x2m−1,(m=1,2,3,...),
x2m+1=b−x2m,(m=0,1,2,...), with x0=a.
45. di=−55cm;m=+1.8
47. di=−41cm,m=1.4
49. proof
51. a. 1di+1do=1f⇒di=3.43m;
b. m=−33.33, so that (2.40×10−2m)(33.33)=80.0cm, and
(3.60×10−2m)(33.33)=1.20m⇒0.800m×1.20m or 80.0cm×120cm
53. a. 1do+1di=1f di=5.08cm;
b. m=−1.695×10−2, so the maximum height is 0.036m1.695×10−2=2.12m⇒100;
c. This seems quite reasonable, since at 3.00 m it is possible to get a full length picture of a person.
55. a. 1do+1di=1f⇒do=2.55m;
b. hiho=−dido⇒ho=1.00m
57. a. Using 1do+1di=1f, di=−56.67cm. Then we can determine the magnification, m=6.67.
b. di=−190cm and m=+20.0;
c. The magnification m increases rapidly as you increase the object distance toward the focal length.
59. 1do+1di=1f
dI=1(1/f)−(1/do)
dido=6.667×10−13=hiho
hi=−0.933mm
61. di=−6.7cm
hi=4.0cm
63. 83 cm to the right of the converging lens, m=−2.3,hi=6.9cm
65. P=52.0D
67. hiho=−dido⇒hi=−ho(dido)=−(3.50mm)(2.00cm30.0cm)=−0.233mm
69. a. P=+62.5D;
b. hiho=−dido⇒hi=−0.250mm;
c. hi=−0.0800mm
71. P=1do+1di⇒do=28.6cm
73. Originally, the close vision was 51.0 D. Therefore, P=1do+1di⇒do=1.00m
75. originally, P=70.0D; because the power for normal distant vision is 50.0 D, the power should be decreased by 20.0 D
77. P=1do+1di⇒do=0.333m
79. a. P=52.0D;
b. P′=56.16D 1do+1di=P⇒do=16.2cm
81. We need di=−18.5cm when do=∞, so P=−5.41D
83. Let x = far point ⇒P=1−(x−0.0175m)+1∞⇒−xP+(0.0175m)P=1⇒x=26.8cm
85. M=6×
87. M=(25cmL)(1+L−ℓf) L−ℓ=do do=13cm
89. M=2.5×
91. M=−2.1×
93. M=25cmf Mmax=5
95. Myoungmax=1+18cmf⇒f=18cmMyoungmax−1
Moldmax=9.8×
97. a. 1do+1di=1f⇒di=4.65cm⇒m=−30.01;
b. Mnet=−240
99. a. 1dobjo+1dobji=1fobj⇒dobji=18.3cm behind the objective lens;
b. mobj=−60.0;
c. deyeo=1.70cm
deyei=−11.3cm;
d. Meye=13.5;
e. Mnet=−810
101. M=−40.0
103. fobj=R2,M=−1.67
105. M=−fobjfeye,feye=+10.0cm
107. Answers will vary.
109. 12 cm to the left of the mirror, m=3/5
111. 27 cm in front of the mirror, m=0.6,hi=1.76cm, orientation upright
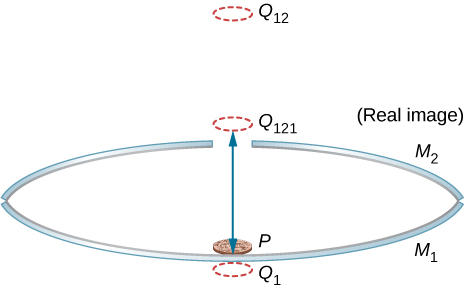
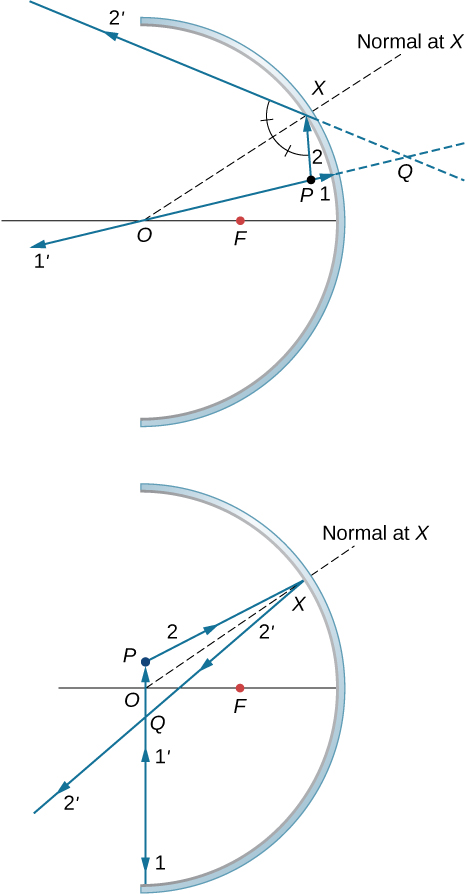
113. The following figure shows three successive images beginning with the image Q1 in mirror M1. Q1 is the image in mirror M1, whose image in mirror M2 is Q12 whose image in mirror M1 is the real image Q121.
115. 5.4 cm from the axis
117. Let the vertex of the concave mirror be the origin of the coordinate system. Image 1 is at −10/3 cm (−3.3 cm), image 2 is at −40/11 cm (−3.6 cm). These serve as objects for subsequent images, which are at −310/83 cm (−3.7 cm), −9340/2501 cm (−3.7 cm), −140,720/37,681 cm (−3.7 cm). All remaining images are at approximately −3.7 cm.
119.
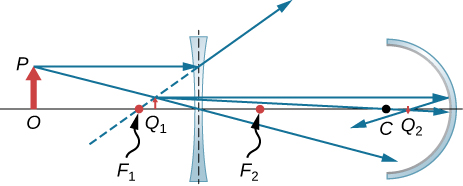
121. Figure shows from left to right: an object with base O on the axis and tip P. A bi-concave lens with focal point F1 and F2 on the left and right respectively and a concave mirror with center of curvature C. Two rays originate from P and diverge through the bi-concave lens. Their back extensions converge between F1 and the lens to form image Q1. Two rays originating from the tip of Q1 strike the mirror, are reflected and converge at Q2 between C and the mirror.
123. −5 D
125. 11
Additional Problems
127. a.
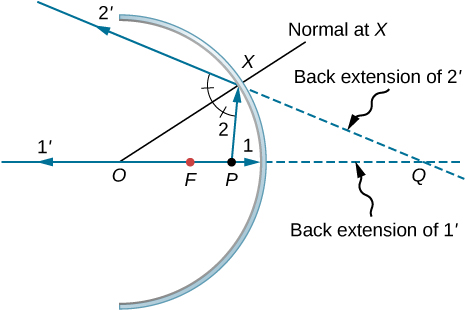
b.
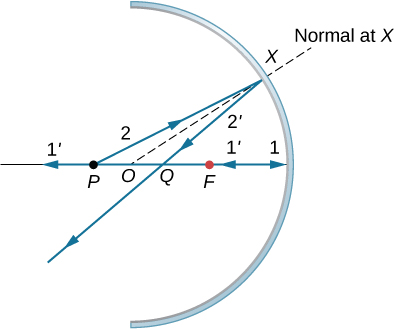
c.
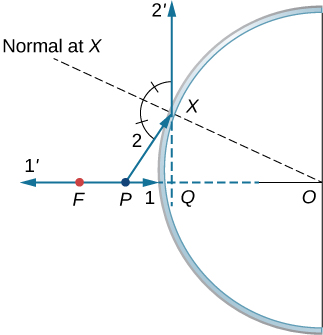
d. similar to the previous picture but with point P outside the focal length;
e. Repeat (a)–(d) for a point object off the axis. For a point object placed off axis in front of a concave mirror corresponding to parts (a) and (b), the case for convex mirror left as exercises.
129. di=−10/3cm,hi=2cm, upright
131. proof
133.
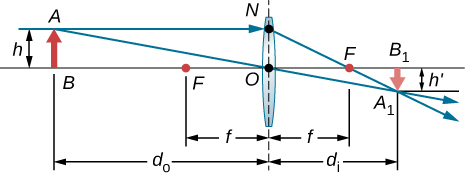
Triangles BAO and B1A1O are similar triangles. Thus, A1B1AB=dido. Triangles NOF and B1A1F are similar triangles. Thus, NOf=A1B1di−f. Noting that NO=AB gives ABf=A1B1di−f or ABA1B1=fdi−f. Inverting this gives A1B1AB=di−ff. Equating the two expressions for the ratio A1B1AB gives dido=di−ff. Dividing through by di gives 1do=1f−1di or 1do+1di=1f.
135. 70 cm
137. The plane mirror has an infinite focal point, so that di=−do. The total apparent distance of the man in the mirror will be his actual distance, plus the apparent image distance, or do+(−di)=2do. If this distance must be less than 20 cm, he should stand at do=10cm.
139. Here we want do=25cm−2.20cm=0.228m. If x=near point, di=−(x−0.0220m). Thus, P=1do+1di=10.228m+1x−0.0220m. Using P=0.75D gives x=0.253m, so the near point is 25.3 cm.
141. Assuming a lens at 2.00 cm from the boy’s eye, the image distance must be di=−(500cm−2.00cm)=−498cm. For an infinite-distance object, the required power is P=1di=−0.200D. Therefore, the −4.00D lens will correct the nearsightedness.
143. 87μm
145. Use, Mnet=−dobji(feye+25cm)fobjfeye. The image distance for the objective is dobji=−Mnetfobjfeyefeye+25cm. Using fobj=3.0cm, feye=10cm, and M=−10 gives dobji=8.6cm. We want this image to be at the focal point of the eyepiece so that the eyepiece forms an image at infinity for comfortable viewing. Thus, the distance d between the lenses should be d=feye+dobji=10cm+8.6cm=19cm
147. a. focal length of the corrective lens fc=−80cm;
b. −1.25 D
149. 2×1016km
151. 105m


