5.5: Newton’s Law of Universal Gravitation
- Last updated
- Jan 14, 2019
- Save as PDF
- Page ID
- 16951

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
The Law of Universal Gravitation
Objects with mass feel an attractive force that is proportional to their masses and inversely proportional to the square of the distance.
learning objectives
- Express the Law of Universal Gravitation in mathematical form
While an apple might not have struck Sir Isaac Newton’s head as myth suggests, the falling of one did inspire Newton to one of the great discoveries in mechanics: The Law of Universal Gravitation. Pondering why the apple never drops sideways or upwards or any other direction except perpendicular to the ground, Newton realized that the Earth itself must be responsible for the apple’s downward motion.
Theorizing that this force must be proportional to the masses of the two objects involved, and using previous intuition about the inverse-square relationship of the force between the earth and the moon, Newton was able to formulate a general physical law by induction.
The Law of Universal Gravitation states that every point mass attracts every other point mass in the universe by a force pointing in a straight line between the centers-of-mass of both points, and this force is proportional to the masses of the objects and inversely proportional to their separation This attractive force always points inward, from one point to the other. The Law applies to all objects with masses, big or small. Two big objects can be considered as point-like masses, if the distance between them is very large compared to their sizes or if they are spherically symmetric. For these cases the mass of each object can be represented as a point mass located at its center-of-mass.
While Newton was able to articulate his Law of Universal Gravitation and verify it experimentally, he could only calculate the relative gravitational force in comparison to another force. It wasn’t until Henry Cavendish’s verification of the gravitational constant that the Law of Universal Gravitation received its final algebraic form:
F=GMmr2
where F represents the force in Newtons, M and m represent the two masses in kilograms, and r represents the separation in meters. G represents the gravitational constant, which has a value of 6.674⋅10−11N(m/kg)2. Because of the magnitude of G, gravitational force is very small unless large masses are involved.

Forces on two masses: All masses are attracted to each other. The force is proportional to the masses and inversely proportional to the square of the distance.
Gravitational Attraction of Spherical Bodies: A Uniform Sphere
The Shell Theorem states that a spherically symmetric object affects other objects as if all of its mass were concentrated at its center.
learning objectives
- Formulate the Shell Theorem for spherically symmetric objects
Universal Gravitation for Spherically Symmetric Bodies
The Law of Universal Gravitation states that the gravitational force between two points of mass is proportional to the magnitudes of their masses and the inverse-square of their separation, d:
F=GmMd2
However, most objects are not point particles. Finding the gravitational force between three-dimensional objects requires treating them as points in space. For highly symmetric shapes such as spheres or spherical shells, finding this point is simple.
The Shell Theorem
Isaac Newton proved the Shell Theorem, which states that:
- A spherically symmetric object affects other objects gravitationally as if all of its mass were concentrated at its center,
- If the object is a spherically symmetric shell (i.e., a hollow ball) then the net gravitational force on a body inside of it is zero.
Since force is a vector quantity, the vector summation of all parts of the shell/sphere contribute to the net force, and this net force is the equivalent of one force measurement taken from the sphere’s midpoint, or center of mass (COM). So when finding the force of gravity exerted on a ball of 10 kg, the distance measured from the ball is taken from the ball’s center of mass to the earth’s center of mass.
Given that a sphere can be thought of as a collection of infinitesimally thin, concentric, spherical shells (like the layers of an onion), then it can be shown that a corollary of the Shell Theorem is that the force exerted in an object inside of a solid sphere is only dependent on the mass of the sphere inside of the radius at which the object is. That is because shells at a greater radius than the one at which the object is, do not contribute a force to an object inside of them (Statement 2 of theorem).
When considering the gravitational force exerted on an object at a point inside or outside a uniform spherically symmetric object of radius RR, there are two simple and distinct situations that must be examined: the case of a hollow spherical shell, and that of a solid sphere with uniformly distributed mass.
Case 1: A hollow spherical shell
The gravitational force acting by a spherically symmetric shell upon a point mass inside it, is the vector sum of gravitational forces acted by each part of the shell, and this vector sum is equal to zero. That is, a mass mm within a spherically symmetric shell of mass M, will feel no net force (Statement 2 of Shell Theorem).
The net gravitational force that a spherical shell of mass M exerts on a body outside of it, is the vector sum of the gravitational forces acted by each part of the shell on the outside object, which add up to a net force acting as if mass M is concentrated on a point at the center of the sphere (Statement 1 of Shell Theorem).
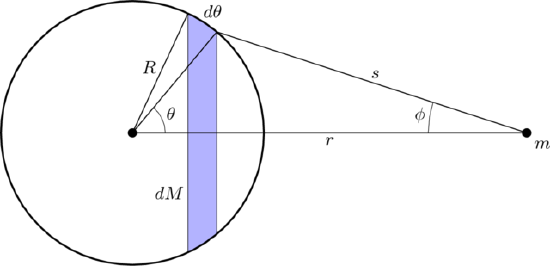
Diagram used in the proof of the Shell Theorem: This diagram outlines the geometry considered when proving The Shell Theorem. In particular, in this case a spherical shell of mass M (left side of figure) exerts a force on mass m (right side of the figure) outside of it. The surface area of a thin slice of the sphere is shown in color. (Note: The proof of the theorem is not presented here. Interested readers can explore further using the sources listed at the bottom of this article.)
Case 2: A solid, uniform sphere
The second situation we will examine is for a solid, uniform sphere of mass M and radius R, exerting a force on a body of mass m at a radius d inside of it (that is, d<R). We can use the results and corollaries of the Shell Theorem to analyze this case. The contribution of all shells of the sphere at a radius (or distance) greater than dd from the sphere’s center-of-mass can be ignored (see above corollary of the Shell Theorem). Only the mass of the sphere within the desired radius M<d(that is the mass of the sphere inside dd) is relevant, and can be considered as a point mass at the center of the sphere. So, the gravitational force acting upon point mass mm is:
F=GmM<dd2
where it can be shown that M<d=43πd3ρ
(ρ is the mass density of the sphere and we are assuming that it does not depend on the radius. That is, the sphere’s mass is uniformly distributed.)
Therefore, combining the above two equations we get:
F=43πGmρd
which shows that mass mm feels a force that is linearly proportional to its distance, dd, from the sphere’s center of mass.
As in the case of hollow spherical shells, the net gravitational force that a solid sphere of uniformly distributed mass M exerts on a body outside of it, is the vector sum of the gravitational forces acted by each shell of the sphere on the outside object. The resulting net gravitational force acts as if mass M is concentrated on a point at the center of the sphere, which is the center of mass, or COM (Statement 1 of Shell Theorem). More generally, this result is true even if the mass M is not uniformly distributed, but its density varies radially (as is the case for planets).
Weight of the Earth
When the bodies have spatial extent, gravitational force is calculated by summing the contributions of point masses which constitute them.
learning objectives
- Describe how gravitational force is calculated for the bodies with spatial extent
Newton’s law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses, and inversely proportional to the square of the distance between them.
In modern language, the law states the following: Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them:
F=Gm1m2r2
where F is the force between the masses, G is the gravitational constant, m1 is the first mass, m2 is the second mass and r is the distance between the centers of the masses.
If the bodies in question have spatial extent (rather than being theoretical point masses), then the gravitational force between them is calculated by summing the contributions of the notional point masses which constitute the bodies. In the limit, as the component point masses become “infinitely small”, this entails integrating the force (in vector form, see below) over the extents of the two bodies.
In this way it can be shown that an object with a spherically-symmetric distribution of mass exerts the same gravitational attraction on external bodies as if all the object’s mass were concentrated at a point at its center.
For points inside a spherically-symmetric distribution of matter, Newton’s Shell theorem can be used to find the gravitational force. The theorem tells us how different parts of the mass distribution affect the gravitational force measured at a point located a distance r0 from the center of the mass distribution:
- The portion of the mass that is located at radii r<r0 causes the same force at r0 as if all of the mass enclosed within a sphere of radius r0 was concentrated at the center of the mass distribution (as noted above).
- The portion of the mass that is located at radii r>r0 exerts no net gravitational force at the distance r0 from the center. That is, the individual gravitational forces exerted by the elements of the sphere out there, on the point at r0 , cancel each other out.
As a consequence, for example, within a shell of uniform thickness and density there is no net gravitational acceleration anywhere within the hollow sphere. Furthermore, inside a uniform sphere the gravity increases linearly with the distance from the center; the increase due to the additional mass is 1.5 times the decrease due to the larger distance from the center. Thus, if a spherically symmetric body has a uniform core and a uniform mantle with a density that is less than 23 of that of the core, then the gravity initially decreases outwardly beyond the boundary, and if the sphere is large enough, further outward the gravity increases again, and eventually it exceeds the gravity at the core/mantle boundary.
The gravity of the Earth may be highest at the core/mantle boundary, as shown in Figure 1:
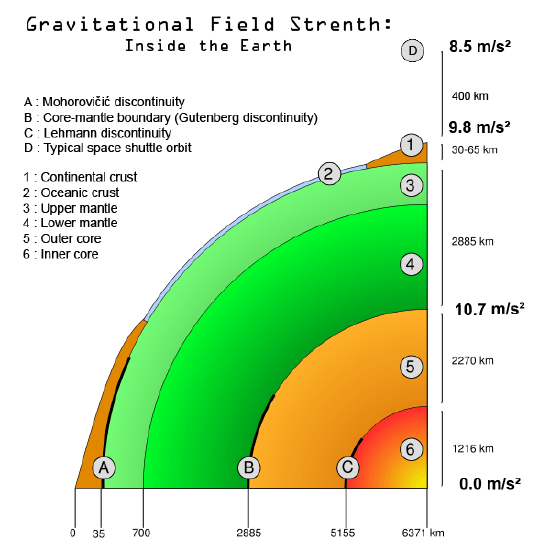
Gravitational Field of Earth: Diagram of the gravitational field strength within the Earth.
Key Points
- Sir Isaac Newton’s inspiration for the Law of Universal Gravitation was from the dropping of an apple from a tree.
- Newton’s insight on the inverse-square property of gravitational force was from intuition about the motion of the earth and the moon.
- The mathematical formula for gravitational force is F=GMmr2 where G is the gravitational constant.
- Since force is a vector quantity, the vector summation of all parts of the shell contribute to the net force, and this net force is the equivalent of one force measurement taken from the sphere’s midpoint, or center of mass (COM).
- The gravitational force on an object within a hollow spherical shell is zero.
- The gravitational force on an object within a uniform spherical mass is linearly proportional to its distance from the sphere’s center of mass (COM).
- Newton’s law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
- The second step in calculating earth’s mass came with the development of Newton’s law of universal gravitation.
- By equating Newton’s second law with his law of universal gravitation, and inputting for the acceleration a the experimentally verified value of 9.8 ms2, the mass of earth is calculated to be 5.96×1024kg, making the earth’s weight calculable given any gravitational field.
- The gravity of the Earth may be highest at the core/mantle boundary
Key Terms
- induction: Use inductive reasoning to generalize and interpret results from applying Newton’s Law of Gravitation.
- inverse: Opposite in effect or nature or order.
- center of mass: The center of mass (COM) is the unique point at the center of a distribution of mass in space that has the property that the weighted position vectors relative to this point sum to zero.
- point mass: A theoretical point with mass assigned to it.
- weight: The force on an object due to the gravitational attraction between it and the Earth (or whatever astronomical object it is primarily influenced by).
- gravitational force: A very long-range, but relatively weak fundamental force of attraction that acts between all particles that have mass; believed to be mediated by gravitons.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Newton's law of universal gravitation. Provided by: WIKIPEDIA. Located at: en.Wikipedia.org/wiki/Newton's_law_of_universal_gravitation. License: CC BY-SA: Attribution-ShareAlike
- Isaac Newton. Provided by: WIKIPEDIA. Located at: en.Wikipedia.org/wiki/Isaac_Newton%23Apple_incident. License: CC BY-SA: Attribution-ShareAlike
- induction. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/induction. License: CC BY-SA: Attribution-ShareAlike
- inverse. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/inverse. License: CC BY-SA: Attribution-ShareAlike
- Shell theorem. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Shell_theorem. License: CC BY-SA: Attribution-ShareAlike
- Center of mass. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Center_of_mass. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Light and Matter. Located at: http://lightandmatter.com/mef.pdf. License: CC BY: Attribution
- Newton's law of universal gravitation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Newton's_law_of_universal_gravitation. License: CC BY-SA: Attribution-ShareAlike
- center of mass. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/center%20of%20mass. License: CC BY-SA: Attribution-ShareAlike
- Shell-diag-1. Provided by: Wikimedia Commons. Located at: commons.wikimedia.org/wiki/File:Shell-diag-1.png. License: CC BY-SA: Attribution-ShareAlike
- Law of universal gravitation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Law_of_universal_gravitation. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42073/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Gravitational constant. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Gravitational_constant. License: CC BY-SA: Attribution-ShareAlike
- Law of universal gravitation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Law_of_universal_gravitation. License: CC BY-SA: Attribution-ShareAlike
- weight. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/weight. License: CC BY-SA: Attribution-ShareAlike
- point mass. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/point_mass. License: CC BY-SA: Attribution-ShareAlike
- gravitational force. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/gravitational_force. License: CC BY-SA: Attribution-ShareAlike
- Shell-diag-1. Provided by: Wikimedia Commons. Located at: https://commons.wikimedia.org/wiki/File:Shell-diag-1.png. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/4/43/Earth-G-force.png. License: CC BY-SA: Attribution-ShareAlike

