1.6: Wave Behavior and Interaction
- Last updated
- Save as PDF
- Page ID
- 17097

- Boundless
- Boundless
learning objectives
- Distinguish transmission and reflection phenomena
When the medium through which a wave travels suddenly changes, the wave often experiences partial transmission and partial refection at the interface. Reflection is a wave phenomenon that changes the direction of a wavefront at an interface between two different media so that the wavefront returns into the medium from which it originated. Transmission permits the passage of wave, with some or none of the incident wave being absorbed. Reflection and transmission often occur at the same time.
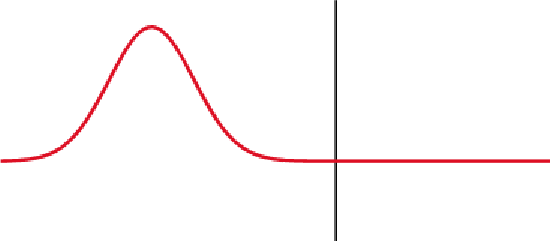
Partial Transmittance and Partial Reflectance: A wave experiences partial transmittance and partial reflectance when the medium through which it travels suddenly changes.
Consider a long string made by connecting two sub-strings with different density \(\mathrm{μ_1,μ_2}\). When the string is driven by an external force, partial reflection and transmission occur as in the figure above. For the incoming, reflected, and transmitted waves, we can try a solution of the following forms:
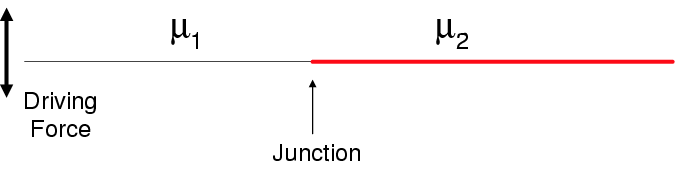
Two Strings With Different Density: Two strings with different density are connected and driven by an external driving force.
\[\begin{align} \mathrm{y_{inc}=A \cos (k_1x−ωt)} \\ \mathrm{y_{ref}=B \cos(k_1x+ωt)} \\ \mathrm{y_{trans}=C \cos (k_2x−ωt)} \end{align}\]
k1 and k2 are determined by the speed of the wave in each medium. We choose our coordinates such that the junction of two sub-strings is located at x=0. In choosing a trial solution for the waves, we assumed that the incident and transmitted waves travel to the right, while the reflected waves travel to the left. (This is why the ‘+’ sign is chosen before ωtωt in the reflected wave. On the left side of the junction, we have
\[\mathrm{y_l=y_{inc}+y_{ref}=A \cos (k_1x−ωt).}\]
On the right side, we have
\[\mathrm{y_r=y_{trans}=C \cos (k_2x−ωt)}\]
We will impose additional restriction on the waves by applying “boundary conditions” at x=0. At the boundary x=0, the wave must be continuous and there should be no kinks in it. Thus we must have
\[\begin{align} \mathrm{y_l(x=0,t)=y_r(x=0,t)} \\ \mathrm{\dfrac{∂y_l(x,t)}{∂x})_{x=0}=(\dfrac{∂y_r(x,t)}{∂x})_{x=0}} \end{align}\]
From the first equation, we get \(\mathrm{A+B = C}\). From the second equation, we get \(\mathrm{A-B = (\frac{k_2}{k_1})C}\).
Thus, we get the following result.
\[\begin{align}\mathrm{A=\dfrac{1}{2}(1+\dfrac{k_2}{k_1})C} \\ \mathrm{B=\dfrac{1}{2}(1−\dfrac{k_2}{k_1})C} \end{align} \]
We can define the transmission (t) and reflection (r) coefficients as
\[\mathrm{t=\dfrac{C}{A}=\dfrac{2k_1}{k_1+k_2}, r=\dfrac{B}{A}=\dfrac{k_1−k_2}{k_1+k_2}.}\]
Superposition and Interference
A wave may have a complicated shape that can result from superposition and interference of several waves.
learning objectives
- Distinguish destructive and constructive interference and identify conditions that are required for the superposition of waves
Most waves do not look very simple. They look are often more complex than the simple water waves often considered in textbooks. Simple waves may be created by a simple harmonic oscillation, and thus have a sinusoidal shape. Complex waves are more interesting, even beautiful, but they look formidable. Most waves appear complex because they result from several simple waves adding together. Luckily, the rules for adding waves are quite simple.

Complex Pattern of Waves: These waves result from the superposition of several waves from different sources, producing a complex pattern.
Superposition
When two or more waves arrive at the same point, they superimpose themselves on one another. More specifically, the disturbances of waves are superimposed when they come together—a phenomenon called superposition. Each disturbance corresponds to a force, and forces add. If the disturbances are along the same line, then the resulting wave is a simple addition of the disturbances of the individual waves—that is, their amplitudes add.
Interference
As a result of superposition of waves, interference can be observed. Interference is an effect caused by two or more waves.
Wave Interference: A brief introduction to constructive and destructive wave interference and the principle of superposition.
When two identical waves arrive at the same point exactly in phase the crests of the two waves are precisely aligned, as are the troughs. This superposition produces pure constructive interference. Because the disturbances add, constructive interference may produce a wave that has twice the amplitude of the individual waves, but has the same wavelength.
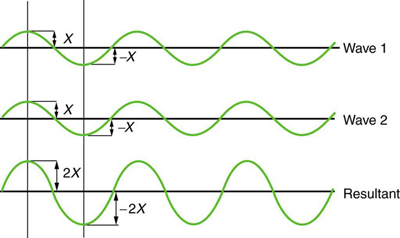
Constructive Interference: Pure constructive interference of two identical waves produces one with twice the amplitude, but the same wavelength.
If two identical waves that arrive exactly out of phase—that is, precisely aligned crest to trough—they may produce pure destructive interference. Because the disturbances are in the opposite direction for this superposition, the resulting amplitude may be zero for destructive interference, and the waves completely cancel.
While pure constructive and pure destructive interference do occur, they require precisely aligned identical waves. The superposition of most waves produces a combination of constructive and destructive interference and can vary from place to place and time to time. Here again, the disturbances add and subtract, producing a more complicated looking wave.
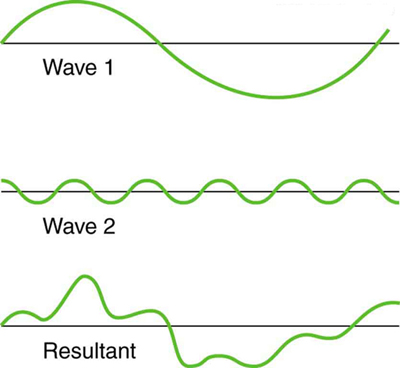
Superposition of Non-Identical Waves: Superposition of non-identical waves exhibits both constructive and destructive interference.
Standing Waves and Resonance
A standing wave is one in which two waves superimpose to produce a wave that varies in amplitude but does not propagate.
learning objectives
- Describe properties of a standing wave
Standing Wave
Sometimes waves do not seem to move, but rather they just vibrate in place. These waves are formed by the superposition of two or more moving waves for two identical waves moving in opposite directions. The waves move through each other with their disturbances adding as they go by. If the two waves have the same amplitude and wavelength then they alternate between constructive and destructive interference. The resultant looks like a wave standing in place and, thus, is called a standing wave.
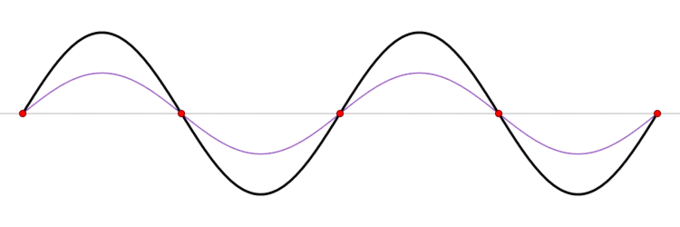
Standing Wave: A standing wave (black) depicted as the sum of two propagating waves traveling in opposite directions (red and blue).
Standing waves are found on the strings of musical instruments and are due to reflections of waves from the ends of the string. shows seven standing waves that can be created on a string that is fixed at both ends. Nodes are the points where the string does not move; more generally, nodes are where the wave disturbance is zero in a standing wave. The fixed ends of strings must be nodes, too, because the string cannot move there. The word antinode is used to denote the location of maximum amplitude in standing waves. Standing waves on strings have a frequency that is related to the propagation speed vw of the disturbance on the string. The wavelength λ is determined by the distance between the points where the string is fixed in place.
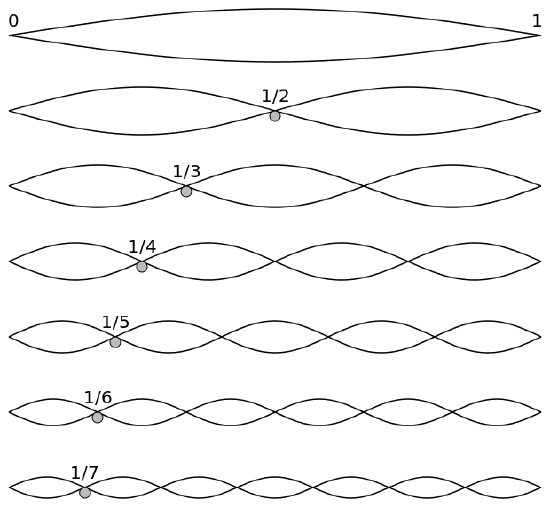
Standing Waves: Standing waves in a string, the fundamental mode and the first six overtones.
The lowest frequency, called the fundamental frequency, is thus for the longest wavelength, twice the length of the string. The overtones or harmonics are multiples of the fundamental frequency. shows the fundamental mode along with six overtones.
Resonance
A closer look at earthquakes provides evidence for conditions appropriate for resonance: standing waves, and constructive and destructive interference. A building may be vibrated for several seconds with a driving frequency matching that of the natural frequency of the vibration of the building—producing a resonance resulting in one building collapsing while neighboring buildings do not. Often buildings of a certain height are devastated while other taller buildings remain intact. The building height matches the condition for setting up a standing wave for that particular height. As the earthquake waves travel along the surface of Earth and reflect off denser rocks, constructive interference occurs at certain points. Often areas closer to the epicenter are not damaged while areas farther away are damaged.
Resonance: A brief overview of resonance, targeted toward introductory physics students.
Harmonic Wave Functions
When vibrations in the string are simple harmonic motion, waves are described by harmonic wave functions.
learning objectives
- Express relationship between the wave number and the wavelength, and frequency and period, of the harmonic wave function
In this Atom we shall consider wave motion resulting from harmonic vibrations and discuss harmonic transverse wave in the context of a string. We assume there is no loss of energy during transmission of wave along the string. This can be approximated when the string is light and taught. In such condition, if we oscillate the free end in harmonic manner, then the vibrations in the string are simple harmonic motion (SHM), perpendicular to the direction of wave motion. The amplitude of wave form remains intact through its passage along the string.
We know that a traveling wave function representing motion in x-direction has the form:
\[\mathrm{y(x,t)=A f(ax−bt).}\]
(Read our Atom on “Mathematical Representation of a Traveling Wave. “) For the case of harmonic vibration, we represent harmonic wave motion in terms of either harmonic sine or cosine function:
\[\mathrm{y(x,t)=A \sin (kx−ωt).}\]
Harmonic Oscillatory Properties
Each particle (or a small segment of string) vibrates in SHM. The particle attains the greatest speed at the mean position and reduces to zero at extreme positions. On the other hand, acceleration of the particle is greatest at extreme positions and zero at the mean position. The vibration of particle is represented by a harmonic sine or cosine function. For x=0:
\[\mathrm{y(x=0,t)=A \sin (ωt)=A \sin (ωt).}\]
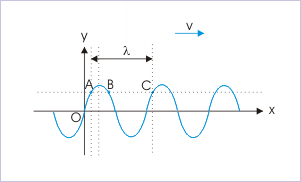
Harmonic Waves: Harmonic waves are described by sinusoidal functions. The wavelength is equal to linear distance between repetitions of transverse disturbance or phase.
Clearly, the displacement in y-direction is described by the bounded sine or cosine function. The important point here is to realize that oscillatory attributes (like time period, angular and linear frequency) of wave motion is same as that of vibration of a particle in transverse direction.
We know that time period in SHM is equal to time taken by the particle to complete one oscillation. It means that displacement of the particle from the mean position at a given position such as x=0 has same value after time period “T” for:
\(\mathrm{ωT=2π}\). Therefore, \(\mathrm{ω=\frac{2π}{T}}\).
Similarly, displacement of the particle from the mean position at a given time such as t=0 has same value by change the position by “, where \(\mathrm{kλ=2π}\). k is called wavenumber.
We can determine speed of the wave by noting that wave travels a linear distance ” in one period (T). Thus, speed of wave is given by:
\[\mathrm{v=\dfrac{λ}{T}=\dfrac{ω}{k}.}\]
Refraction
Refraction is a surface phenomenon that occurs as the change in direction of a wave due to a change in its medium.
learning objectives
- Formulate the law of conservation of energy and momentum as it is applied to refraction
Refraction is the change in direction of a wave due to a change in its medium. Essentially, it is a surface phenomenon—mainly in governance to the law of conservation of energy and momentum. Due to change of medium, the phase velocity of the wave is changed but its frequency remains constant (most commonly observed when a wave passes from one medium to another at any angle other than 90° or 0°). Refraction of light is the most commonly observed phenomenon, but any type of wave can refract when it interacts with a medium (e.g., when sound waves pass from one medium into another or when water waves move into water of a different depth). Refraction is described by Snell’s law, which states that for a given pair of media and a wave with a single frequency, the ratio of the sines of the angle of incidence θ1 and angle of refraction θ2 is equivalent to the ratio of phase velocities (v1/v2) in the two media, or equivalently, to the opposite ratio of the indices of refraction (n2/n1):
\[\mathrm{\dfrac{\sin θ_1 }{\sin θ_2}=\dfrac{v_1}{v_2}=\dfrac{n_2}{n_1}.}\]
In optics, refraction is a phenomenon that often occurs when waves travel from a medium with a given refractive index to a medium with another at an oblique angle. For example, a light ray will refract as it enters and leaves glass, assuming there is a change in refractive index. A ray traveling along the normal (perpendicular to the boundary) will change speed, but not direction. Refraction still occurs in this case. Understanding of refraction led to the invention of lenses and the refracting telescope.
Refraction can be seen when looking into a bowl of water, as illustrated in. Air has a refractive index of about 1.0003, and water has a refractive index of about 1.33. If a person looks at a straight object, such as a pencil or straw, placed partially in the water at a slant, the object appears to bend at the water’s surface. This is due to the bending of light rays as they move from the water to the air. Once the rays reach the eye, the eye traces them back as straight lines (lines of sight). The lines of sight (shown as dashed lines) intersect at a higher position than where the actual rays originated (causing the pencil to appear higher and the water to appear shallower than they actually are).
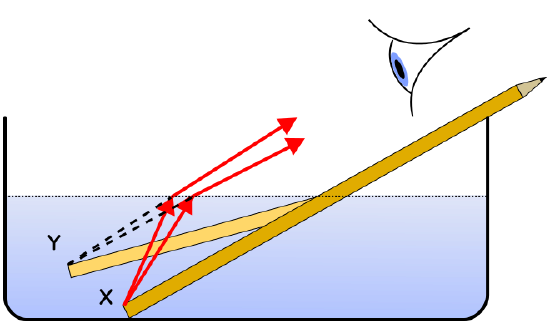
Refraction in Water: An object (in this case a pencil) partially immersed in water looks bent due to refraction: the light waves from X change direction and so seem to originate at Y. (More accurately, for any angle of view, Y should be vertically above X, and the pencil should appear shorter, not longer as shown. )
Diffraction
Diffraction refers to various phenomena such as the bending of waves around obstacles and the spreading out of waves past small openings.
learning objectives
- Describe the phenomenon of diffraction, according to classical physics
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. In classical physics, the diffraction phenomenon is described as the apparent bending of waves around small obstacles and the spreading out of waves past small openings. Similar effects occur when a light wave travels through a medium with a varying refractive index, or a sound wave travels through one with varying acoustic impedance.
Diffraction occurs with all waves, including sound waves, water waves, and electromagnetic waves such as visible light, X-rays and radio waves. As physical objects have wave-like properties (at the atomic level), diffraction also occurs with matter and can be studied according to the principles of quantum mechanics.
Diffraction effects are generally most pronounced for waves whose wavelengths are roughly similar to the dimensions of the diffracting objects. If the obstructing object provides multiple, closely-spaced openings, a complex pattern of varying intensity can result. This is due to the superposition, or interference, of different parts of a wave that travel to the observer by different paths. A good example would be diffraction gratings.

Intensity Pattern: Intensity pattern formed on a screen by diffraction from a square aperture.
The effects of diffraction are often seen in everyday life. The most striking examples of diffraction are those involving light. For example, the closely spaced tracks on a CD or DVD act as a diffraction grating to form the familiar rainbow pattern seen when looking at a disk. This principle can be extended to engineer a grating with a structure such that it will produce any diffraction pattern desired, like the hologram on a credit card. Diffraction in the atmosphere by small particles can cause a bright ring to be visible around a bright light source like the sun or the moon. A shadow of a solid object, using light from a compact source, shows small fringes near its edges. The speckle pattern which is observed when laser light falls on an optically rough surface is also a diffraction phenomenon. All these effects are a consequence of the fact that light propagates as a wave.
Mathematical Represenation of a Traveling Wave
The most general solution of the wave equation \(\mathrm{\frac{∂^2u}{∂t^2}=c^2\frac{∂^2u}{∂x^2}}\) is given as \(\mathrm{u(x,t)=f(x+ct)+g(x−ct)}\), where f and g are arbitrary functions.
learning objectives
- Formulate solution of the wave equation for a traveling wave
In general, one dimensional waves satisfy the 1D wave equation:
\[\mathrm{\dfrac{∂^2u}{∂t^2}=c^2\dfrac{∂^2u}{∂x^2}.}\]
For example, a sinusoidal form
\[\mathrm{u(x,t)=A \sin (kx−ωt)}\]
is a solution of the wave equation for \(\mathrm{c=\frac{ω}{k}}\). In this atom, we will obtain a general mathematical form of a traveling wave.
Solving the Wave Equation
First, we notice that any function u(x,t) satisfying
\[\mathrm{\dfrac{∂u}{∂t}=±c\dfrac{∂u}{∂x} (Eq. 1)}\]
is a solution to the wave equation. To show this, note that
\[\begin{align} \mathrm{\dfrac{∂^2u}{∂t^2}} & \mathrm{=\dfrac{∂}{∂t}(\dfrac{∂u}{∂t})=±c\dfrac{∂}{∂t}(\dfrac{∂u}{∂x})} \\ & \mathrm{=±c\dfrac{∂}{∂x}(\dfrac{∂u}{∂t})=c^2\dfrac{∂^2u}{∂x^2}.} \end{align}\]
In the middle, we used the equation 1 along with the fact that partial derivatives are interchangeable.
To solve the equation 1, let’s introduce new variables: \(\mathrm{ϕ=x−ct,ψ=x+ct.}\) From the chain rules,
\[\mathrm{\dfrac{∂}{∂t}=\dfrac{∂ϕ}{∂t}\dfrac{∂}{∂ϕ}+\dfrac{∂ψ}{∂t}\dfrac{∂}{∂ψ}=−c\dfrac{∂}{∂ϕ}+c\dfrac{∂}{∂ψ}.}\]
\[\mathrm{\dfrac{∂}{∂x}=\dfrac{∂ϕ}{∂x}\dfrac{∂}{∂ϕ}+\dfrac{∂ψ}{∂x}\dfrac{∂}{∂ψ}=\dfrac{∂}{∂ϕ}+\dfrac{∂}{∂ψ}.}\]
With the change of variables, the equation 1 becomes \(\mathrm{\frac{∂u_+}{∂ϕ}=0}\) for the equation with the “+” sign and \(\mathrm{\frac{∂u_−}{∂ψ}=0}\) for the “-” sign. Therefore, we see that
\[\mathrm{u_+(ϕ,ψ)=f(ψ),u_−(ϕ,ψ)=g(ϕ),}\]
where f and g are arbitrary functions. Converting back to the original variables of x and t, we conclude that the solution of the original wave equation is
\[\mathrm{u(x,t)=f(x+ct)+g(x−ct).}\]
f(x+ct) represents a left-going traveling wave, while g(x-ct) represents a right-going traveling wave. In other words, solutions of the 1D wave equation are sums of a left traveling function f and a right traveling function g. “Traveling” means that the shape of these individual arbitrary functions with respect to x stays constant, however the functions are translated left and right with time at the speed c. This solution was derived by Jean le Rond d’Alembert.
Boundary Condition
Any function that contains “x+ct” or “x-ct” can be a solution of the wave equation. The wave function is further determined by taking additional information, usually given as boundary conditions and some others. For example, in the case of a string in a guitar, we know that the wave has zero amplitude at both ends: u(x=0)=u(x=L)=0. Also, the shape of the function at an instance can be provided to determine the function.
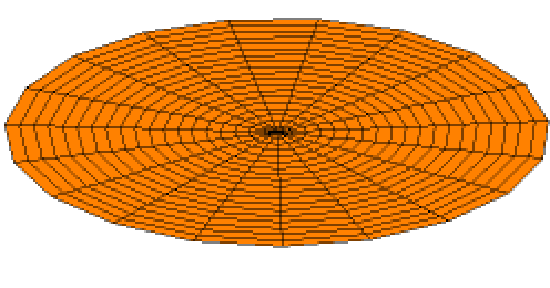
Wave Equation in Two Dimensions: A solution of the wave equation in two dimensions with a zero-displacement boundary condition along the entire outer edge.
Energy, Intensity, Frequency, and Amplitude
The energy in a wave is proportional to its amplitude squared and the intensity of a wave is defined as power per unit area.
learning objectives
- Describe relationship between the energy and the amplitude, and energy and intensity, of a wave
All waves carry energy. This is seen in practical applications (e.g., in medicine), as well as effects in nature. Some examples of are:
- ultrasound used for deep-heat treatment of muscle strains
- a laser beam to burn away malignant tissue
- water waves that erode beaches
- earthquakes that topple cities
The amount of energy in a wave is related to its amplitude. Large-amplitude earthquakes produce large ground displacements, as seen in. Loud sounds have higher pressure amplitudes and come from larger-amplitude source vibrations than soft sounds. Large ocean breakers erode the shore more than small ones. More quantitatively, a wave is a displacement that is resisted by a restoring force. The larger the displacement x, the larger the force F=-kx needed to create it. Because work W is related to force multiplied by distance (Fx) and energy is put into the wave by the work done to create it, the energy in a wave is related to amplitude. In fact, a wave’s energy is directly proportional to its amplitude squared because:

Earthquake Destruction: The destructive effect of an earthquake is palpable evidence of the energy carried in these waves. The Richter scale rating of earthquakes is related to both their amplitude and the energy they carry.
\[\mathrm{W=∫F(x)dx=\frac{1}{2}kx^2.}\]
The energy effects of a wave depend on time as well as amplitude. For example, the longer deep-heat ultrasound is applied, the more energy it transfers. Therefore, power is more appropriate than energy to describe the “intensity” of a wave. Waves can also be concentrated or spread out. Sunlight, for example, can be focused to burn wood. Earthquakes “spread out” so they do less damage the farther they spread from their source. In both cases, changing the area the waves cover has important effects. All these pertinent factors are included in the definition of intensity I as power (P) per unit area:
\[\mathrm{I=\dfrac{P}{A},}\]
where P is the power carried by the wave through area A.
Energy vs. Frequency
In classic wave theory, energy of a wave doesn’t depend on the frequency of the wave. However, this is not the case in the microscopic world, as shown in experiments on photoelectric effects (see our Atom on “Photoelectric Effect”). As Einstein postulated to explain photoelectric effects, a quantum of light (photon) carries a specific amount of energy proportional to the frequency of light. Although you can increase the number of photons by increasing the intensity of a beam, the energy of individual photons in the beam is determined by the frequency of the beam.
Key Points
- Reflection is a wave phenomenon that changes the direction of a wavefront at an interface between two different media so that the wavefront returns into the medium from which it originated.
- At the boundary, a wave must be continuous and there should be no kinks in it.
- By imposing boundary conditions, we can solve wave equation and get the form of the waves. Reflection and transmission coefficients are defined as ratio of reflected/transmitted amplitudes and the incoming amplitude.
- The disturbances of waves are superimposed when they come together—a phenomenon called superposition.
- As a result of superposition of waves, inteference can be observed. Interference is an effect caused by two or more waves. Waves can interfere constructively or destructively.
- The superposition of most waves produces a combination of constructive and destructive interference and can vary from place to place and time to time.
- If two waves with the same amplitude and wavelength travel in opposite directions they alternate between constructive and destructive interference. The resultant looks like a wave standing in place and, thus, is called a standing wave.
- Nodes are points of no motion in standing waves. An antinode is the location of maximum amplitude of a standing wave.
- During an earthquake, buildings with a certain height may collapse more easily. This occurs when the building height matches the condition for setting up a standing wave for that particular height.
- We represent harmonic wave motion in terms of either harmonic sine or cosine function: \(\mathrm{y(x,t)=A \sin (kx−ωt)}\).
- k and ω in the harmonic wave functinon are related to wavelength and period as follows: \(\mathrm{k=\frac{2π}{λ}, ω=\frac{2π}{T}.}\)
- The speed of a harmonic wave is given by ω/k.
- Refraction is mainly in governance to the law of conservation of energy and momentum. Due to change of medium, the phase velocity of the wave is changed but its frequency remains constant.
- Refraction is described by Snell’s law, which states that for a given pair of media and a wave with a single frequency, \(\mathrm{\frac{\sin θ_1}{ \sin θ_2}=\frac{v_1}{v_2}=\frac{n_2}{n_1}.}\)
- An object partially immersed in water looks bent due to refraction.
- Diffraction is a wave phenomenon. It occurs with all waves, including sound waves, water waves, and electromagnetic waves such as visible light, X-rays and radio waves.
- Diffraction effects are generally most pronounced for waves whose wavelengths are roughly similar to the dimensions of the diffracting objects.
- The effects of diffraction are often seen in everyday life. All these effects are a consequence of the fact that light propagates as a wave.
- Any function u(x,t) satisfying \(\mathrm{\frac{∂u}{∂t}=±c\frac{∂u}{∂x}}\) is a solution the wave equation. To solve this new equation, we introduced new variables \(\mathrm{ϕ=x−ct,ψ=x+ct}\).
- The solutions of the 1D wave equation are sums of a left traveling function and a right traveling function.
- The wave function is further determined by taking additional information, usually given as boundary conditions and some others.
- The energy effects of a wave depend on the amplitude and duration (time) of the wave. Waves can also be concentrated or spread out. Considering all these factors, intensity is defined as power per unit area.
- In the classical wave theory, energy of a wave doesn’t depend on the frequency of the wave. However, the energy of individual photons in a beam is determined by the frequency of the beam.
- Wave’s energy is directly proportional to its amplitude squared.
Key Terms
- boundary condition: A set of restraints at the boundaries, used to solve a differential equation.
- superposition: The summing of two or more field contributions occupying the same space.
- interference: An effect caused by the superposition of two systems of waves, such as a distortion on a broadcast signal due to atmospheric or other effects.
- constructive interference: Occurs when waves interfere with each other crest to crest and the waves are exactly in phase with each other.
- destructive interference: Occurs when waves interfere with each other crest to trough (peak to valley) and are exactly out of phase with each other.
- resonance: The increase in the amplitude of an oscillation of a system under the influence of a periodic force whose frequency is close to that of the system’s natural frequency.
- simple harmonic motion: (SHM) — Oscillating motion (as of a pendulum) in which the acceleration of the oscillator has an equal magnitude but opposite direction to the displacement of it from the equilibrium position.
- Snell’s law: A formula used to describe the relationship between the angles of incidence and refraction.
- refractive index: The ratio of the speed of light in air or vacuum to that in another medium.
- wave equation: An important second-order linear partial differential equation for the description of waves such as sound waves, light waves, and water waves.
- Restoring force: If the system is perturbed away from the equilibrium, the restoring force will tend to bring the system back toward equilibrium. The restoring force is a function only of position of the mass or particle. It is always directed back toward the equilibrium position of the system.An example is the action of a spring. An idealized spring exerts a force that is proportional to the amount of deformation of the spring from its equilibrium length, exerted in a direction to oppose the deformation. Pulling the spring to a greater length causes it to exert a force that brings the spring back toward its equilibrium length. The amount of force can be determined by multiplying the spring constant of the spring by the amount of stretch.
- ultrasound: Sound with a frequency greater than the upper limit of human hearing; approximately 20 kilohertz.
- photoelectric effects: In photoelectric effects, electrons are emitted from matter (metals and non-metallic solids, liquids or gases) as a consequence of their absorption of energy from electromagnetic radiation.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Paul Padley, Reflection and Transmission of Mechanical Waves. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12794/latest/. License: CC BY: Attribution
- boundary condition. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/boundary%20condition. License: CC BY-SA: Attribution-ShareAlike
- Transmission (wave propagation). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Transmission_(wave_propagation). License: CC BY: Attribution
- Paul Padley, Reflection and Transmission of Mechanical Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12794/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/superposition. License: CC BY-SA: Attribution-ShareAlike
- interference. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/interference. License: CC BY-SA: Attribution-ShareAlike
- Transmission (wave propagation). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Transmission_(wave_propagation). License: CC BY: Attribution
- Paul Padley, Reflection and Transmission of Mechanical Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12794/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- Wave Interference. Located at: http://www.youtube.com/watch?v=tsmwLFgibT4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Superposition and Interference. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/constructive-interference. License: CC BY-SA: Attribution-ShareAlike
- resonance. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/resonance. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/destructive-interference. License: CC BY-SA: Attribution-ShareAlike
- Transmission (wave propagation). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Transmission_(wave_propagation). License: CC BY: Attribution
- Paul Padley, Reflection and Transmission of Mechanical Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12794/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- Wave Interference. Located at: http://www.youtube.com/watch?v=tsmwLFgibT4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Resonance. Located at: http://www.youtube.com/watch?v=YYlpePXdiCg. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Transverse Harmonic Waves. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m15992/latest/. License: CC BY: Attribution
- simple harmonic motion. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/simple_harmonic_motion. License: CC BY-SA: Attribution-ShareAlike
- Transmission (wave propagation). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Transmission_(wave_propagation). License: CC BY: Attribution
- Paul Padley, Reflection and Transmission of Mechanical Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12794/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- Wave Interference. Located at: http://www.youtube.com/watch?v=tsmwLFgibT4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Resonance. Located at: http://www.youtube.com/watch?v=YYlpePXdiCg. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Transverse Harmonic Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m15992/latest/. License: CC BY: Attribution
- Refraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Refraction. License: CC BY-SA: Attribution-ShareAlike
- Snell's law. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Snell's%20law. License: CC BY-SA: Attribution-ShareAlike
- refractive index. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/refractive_index. License: CC BY-SA: Attribution-ShareAlike
- Transmission (wave propagation). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Transmission_(wave_propagation). License: CC BY: Attribution
- Paul Padley, Reflection and Transmission of Mechanical Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12794/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- Wave Interference. Located at: http://www.youtube.com/watch?v=tsmwLFgibT4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Resonance. Located at: http://www.youtube.com/watch?v=YYlpePXdiCg. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Transverse Harmonic Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m15992/latest/. License: CC BY: Attribution
- Refraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Refraction. License: CC BY: Attribution
- Diffraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Diffraction. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/superposition. License: CC BY-SA: Attribution-ShareAlike
- interference. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/interference. License: CC BY-SA: Attribution-ShareAlike
- Transmission (wave propagation). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Transmission_(wave_propagation). License: CC BY: Attribution
- Paul Padley, Reflection and Transmission of Mechanical Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12794/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- Wave Interference. Located at: http://www.youtube.com/watch?v=tsmwLFgibT4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Resonance. Located at: http://www.youtube.com/watch?v=YYlpePXdiCg. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Transverse Harmonic Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m15992/latest/. License: CC BY: Attribution
- Refraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Refraction. License: CC BY: Attribution
- Diffraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Diffraction. License: CC BY: Attribution
- Wave equation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Wave_equation. License: CC BY-SA: Attribution-ShareAlike
- boundary condition. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/boundary%20condition. License: CC BY-SA: Attribution-ShareAlike
- wave equation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/wave%20equation. License: CC BY-SA: Attribution-ShareAlike
- Transmission (wave propagation). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Transmission_(wave_propagation). License: CC BY: Attribution
- Paul Padley, Reflection and Transmission of Mechanical Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12794/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- Wave Interference. Located at: http://www.youtube.com/watch?v=tsmwLFgibT4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Resonance. Located at: http://www.youtube.com/watch?v=YYlpePXdiCg. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Transverse Harmonic Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m15992/latest/. License: CC BY: Attribution
- Refraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Refraction. License: CC BY: Attribution
- Diffraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Diffraction. License: CC BY: Attribution
- Wave equation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Wave_equation. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42250/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Restoring force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Restoring%20force. License: CC BY-SA: Attribution-ShareAlike
- photoelectric effects. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/photoelectric%20effects. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//biology/definition/ultrasound. License: CC BY-SA: Attribution-ShareAlike
- Transmission (wave propagation). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Transmission_(wave_propagation). License: CC BY: Attribution
- Paul Padley, Reflection and Transmission of Mechanical Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12794/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- OpenStax College, Superposition and Interference. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42249/latest/. License: CC BY: Attribution
- Wave Interference. Located at: http://www.youtube.com/watch?v=tsmwLFgibT4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Standing wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Standing_wave. License: CC BY: Attribution
- Resonance. Located at: http://www.youtube.com/watch?v=YYlpePXdiCg. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Transverse Harmonic Waves. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m15992/latest/. License: CC BY: Attribution
- Refraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Refraction. License: CC BY: Attribution
- Diffraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Diffraction. License: CC BY: Attribution
- Wave equation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Wave_equation. License: CC BY: Attribution
- OpenStax College, College Physics. February 7, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42250/latest/?collection=col11406/1.7. License: CC BY: Attribution

