learning objectives
- Calculate the speed of a wave on a string
When studying waves, it is helpful to use a string to observe the physical properties of waves visually. Imagine you are holding one end of a string, and the other end is secured and the string is pulled tight. Now, if you were to flick the string either up and down. The wave that occurs due to this motion is called a transverse wave. A transverse wave is defined as a wave where the movement of the particles of the medium is perpendicular to the direction of the propagation of the wave. Figure 1 shows this in a diagram. In this case, the medium through which the waves propagate is the rope. The wave traveled from one end to the other, while the rope moved up and down.
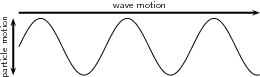
Figure 1: In transverse waves, the media the wave is traveling in moves perpendicular to the direction of the wave.
Wave Properties
Transverse waves have what are called peaks and troughs. The peak is the crest, or top point of the wave and the trough is the valley or bottom point of the wave. Refer to Figure 2 for a visual representation of these terms.The amplitude is the maximum displacement of a particle from its equilibrium position.Wavelength, usually denoted with a lambda (λ) and measured in meters, is the distance from either one peak to the next peak, or one trough to the next trough.Period, usually denoted as T and measured in seconds, is the time it takes for two successive peaks, or one wavelength, to pass through a fixed point.Frequency, f, is the number of wavelengths that pass through a given point in 1 second. Frequency is measured by taking the reciprocal of a period: \(\mathrm{f=\frac{1}{T}}\)
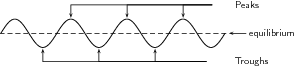
Figure 2: Peaks are the top most points of the waves and troughs are the bottom, or valleys of the waves.
Speed of a Wave on a String
Velocity is found by dividing the distance traveled by the time it took to travel that distance. In waves, this is found by dividing the wavelength by the period: v=λTv=λTWe can take the inverse proportionality to period and frequency and apply it to this situation:
\[\begin{align} & \mathrm{v=\dfrac{λ}{T}} \\ & \mathrm{ v=λ\dfrac{1}{T}} \\ & \mathrm{ v=λf} \end{align}\]
Speed of a Wave on a Vibrating String
Another example of waves on strings are of the waves on vibrating strings, such as in musical instruments. Pianos and guitars both use vibrating strings to produce music. In these cases, the frequency is what characterizes the pitch and therefore the note. The speed of a wave on this kind of string is proportional to the square root of the tension in the string and inversely proportional to the square root of the linear density of the string:\(\mathrm{v=\sqrt{\frac{T}{μ}}}\)
Reflections
When transverse waves in strings meet one end, they are reflected, and when the incident wave meets the reflected wave, interference occurs.
learning objectives
- Explain when a standing wave occurs
Overview
Imagine you are holding one end of a string, and the other end is secured and the string is pulled tight. Now, if you were to flick the string either up and down. The wave that occurs due to this motion is called a transverse wave. A transverse wave is defined as a wave where the movement of the particles of the medium is perpendicular to the direction of the propagation of the wave. shows this in a diagram. In this case, the medium through which the waves propagate is the rope. The wave traveled from one end to the other, while the rope moved up and down.
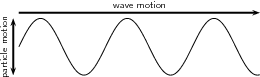
Transverse Wave: Diagram of a transverse wave. The wave motion moves perpendicular to the medium it is traveling in.
Properties of Waves
- Transverse waves have what are called peaks and troughs. The peak is the crest, or top point of the wave and the trough is the valley or bottom point of the wave.
- The amplitude is the maximum displacement of a particle from its equilibrium position.
- Wavelength, usually denoted with a lambda (λ) and measured in meters, is the distance from either one peak to the next peak, or one trough to the next trough.
- Period, usually denoted as T and measured in seconds, is the time it takes for two successive peaks, or one wavelength, to pass through a fixed point.
- Frequency, f, is the number of wavelengths that pass through a given point in 1 second. Frequency is measured by taking the reciprocal of a period: \(\mathrm{f=\frac{1}{T}}\)
- Transverse waves can occur while being fixed at the end point or while being free at the end point.
Reflections of Transverse Waves
The way in which a transverse wave reflects depends on whether or not it is fixed at both ends. First we will look at waves that are fixed at both ends:
shows an image of a transverse wave that is reflected from a fixed end. When a transverse wave meets a fixed end, the wave is reflected, but inverted. This swaps the peaks with the troughs and the troughs with the peaks.

Transverse Wave With a Fixed End Point: A transverse wave that is fixed at the end point. The reflected wave is inverted.
is an image of a transverse wave on a string that meets a free end. The wave is reflected, but unlike a transverse wave with a fixed end, it is not inverted.

Transverse Wave With a Free End: When a transverse wave meets a free end, it is reflected.
Standing Waves
When either of the two scenarios of wave reflection occurs, the incident wave meets the reflected wave. These waves move past each other in opposite directions, causing interference. When these two waves have the same frequency, the product of this is called the standing waves. Standing waves appear to be standing still, hence the name. To understand how standing waves occur, we can analyze them further: When the incident wave and reflected wave first meet, both waves have an amplitude is zero. As the waves continue to move past each other, they continue to interfere with each other either constructively of destructively.
As you may remember from previous atoms, when waves are completely in phase and interfere with each other constructively, they are amplified, and when they are completely out of phase and interfere destructively they cancel out. As the waves continue to move past each other, and are reflected from the opposite end, they continue to interfere both ways, and a standing wave is produced.
Every point in the medium containing a standing wave oscillates up and down and the amplitude of the oscillations depends on the location of the point. When we observe standing waves on strings, it looks like the wave is not moving and standing still. The principle of standing waves is the basis of resonance and how many musical instruments get their sound. The points in a standing wave that appear to remain flat and do not move are called nodes. The points which reach the maximum oscillation height are called antinodes.
Key Points
- The type of wave that occurs in a string is called a transverse wave. In a transverse wave, the wave direction is perpendicular the the direction that the string oscillates in.
- The period of a wave is indirectly proportional to the frequency of the wave: \(\mathrm{T=\frac{1}{f}}\).
- The speed of a wave is proportional to the wavelength and indirectly proportional to the period of the wave: \(\mathrm{v=\frac{λ}{T}}\).
- This equation can be simplified by using the relationship between frequency and period:\(\mathrm{v=λf}\).
- When a transverse wave on a string is fixed at the end point, the reflected wave is inverted from the incident wave. When a transverse wave on a string is free at the end point, the reflected wave is not inverted from the incident wave.
- A standing wave occurs when an incident wave meets a reflected wave on a string.
- The points in a standing wave that appear to remain flat and do not move are called nodes. The points which reach the maximum oscillation height are called antinodes.
- Every point in the medium containing a standing wave oscillates up and down and the amplitude of the oscillations depends on the location of the point.
- A standing wave has some points that remain flat due to destructive interference. These are called antinodes.
- The points on a standing wave that have reached maximum oscillation do so from constructive interference, and are called nodes.
Key Terms
- transverse wave: Any wave in which the direction of disturbance is perpendicular to the direction of travel.
- oscillate: To swing back and forth, especially if with a regular rhythm.
- amplitude: The maximum absolute value of some quantity that varies.
- standing wave: A wave form which occurs in a limited, fixed medium in such a way that the reflected wave coincides with the produced wave. A common example is the vibration of the strings on a musical stringed instrument.
- transverse wave: Any wave in which the direction of disturbance is perpendicular to the direction of travel.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Rory Adams (Free High School Science Texts Project), Mark Horner, and Heather Williams, Transverse Waves - Grade 10. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m32635/latest/. License: CC BY: Attribution
- Wave. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Wave%23Waves_on_strings. License: CC BY-SA: Attribution-ShareAlike
- Vibrating string. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Vibrating_string. License: CC BY-SA: Attribution-ShareAlike
- oscillate. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/oscillate. License: CC BY-SA: Attribution-ShareAlike
- transverse wave. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/transverse_wave. License: CC BY-SA: Attribution-ShareAlike
- Rory Adams (Free High School Science Texts Project), Mark Horner, and Heather Williams, Transverse Waves - Grade 10. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m32635/latest/. License: CC BY: Attribution
- Rory Adams (Free High School Science Texts Project), Mark Horner, and Heather Williams, Transverse Waves - Grade 10. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m32635/latest/. License: CC BY: Attribution
- Rory Adams (Free High School Science Texts Project), Mark Horner, and Heather Williams, Transverse Waves - Grade 10. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m32635/latest/. License: CC BY: Attribution
- amplitude. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/amplitude. License: CC BY-SA: Attribution-ShareAlike
- transverse wave. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/transverse_wave. License: CC BY-SA: Attribution-ShareAlike
- standing wave. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/standing_wave. License: CC BY-SA: Attribution-ShareAlike
- Rory Adams (Free High School Science Texts Project), Mark Horner, and Heather Williams, Transverse Waves - Grade 10. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m32635/latest/. License: CC BY: Attribution
- Rory Adams (Free High School Science Texts Project), Mark Horner, and Heather Williams, Transverse Waves - Grade 10. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m32635/latest/. License: CC BY: Attribution
- Rory Adams (Free High School Science Texts Project), Mark Horner, and Heather Williams, Transverse Waves - Grade 10. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m32635/latest/. License: CC BY: Attribution
- Rory Adams (Free High School Science Texts Project), Mark Horner, and Heather Williams, Transverse Waves - Grade 10. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m32635/latest/. License: CC BY: Attribution
- Rory Adams (Free High School Science Texts Project), Mark Horner, and Heather Williams, Transverse Waves - Grade 10. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m32635/latest/. License: CC BY: Attribution






