4.6: Vector Nature of Forces
- Last updated
- Jan 14, 2019
- Save as PDF
- Page ID
- 16944

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
Forces in Two Dimensions
Forces act in a particular direction and have sizes dependent upon how strong the push or pull is.
learning objectives
- Explain why forces are classified as “vector quantities”
Forces act in a particular direction and have sizes dependent upon how strong the push or pull is. Because of these characteristics, forces are classified as “vector quantities. ” This means that forces follow a different set of mathematical rules than physical quantities that do not have direction (denoted scalar quantities).
For example, when determining what happens when two forces act on the same object, it is necessary to know both the magnitude and the direction of both forces to calculate the result. If both of these pieces of information are not known for each force, the situation is ambiguous. For example, if you know that two people are pulling on the same rope with known magnitudes of force but you do not know which direction either person is pulling, it is impossible to determine what the acceleration of the rope will be. The two people could be pulling against each other as in tug of war or the two people could be pulling in the same direction. In this simple one-dimensional example, without knowing the direction of the forces it is impossible to decide whether the net force is the result of adding the two force magnitudes or subtracting one from the other. Associating forces with vectors avoids such problems.
When two forces act on a point particle, the resulting force or the resultant (also called the net force) can be determined by following the parallelogram rule of vector addition: the addition of two vectors represented by sides of a parallelogram gives an equivalent resultant vector which is equal in magnitude and direction to the transversal of the parallelogram. The magnitude of the resultant varies from the difference of the magnitudes of the two forces to their sum, depending on the angle between their lines of action.
Free-body diagrams can be used as a convenient way to keep track of forces acting on a system. Ideally, these diagrams are drawn with the angles and relative magnitudes of the force vectors preserved so that graphical vector addition can be done to determine the net force.
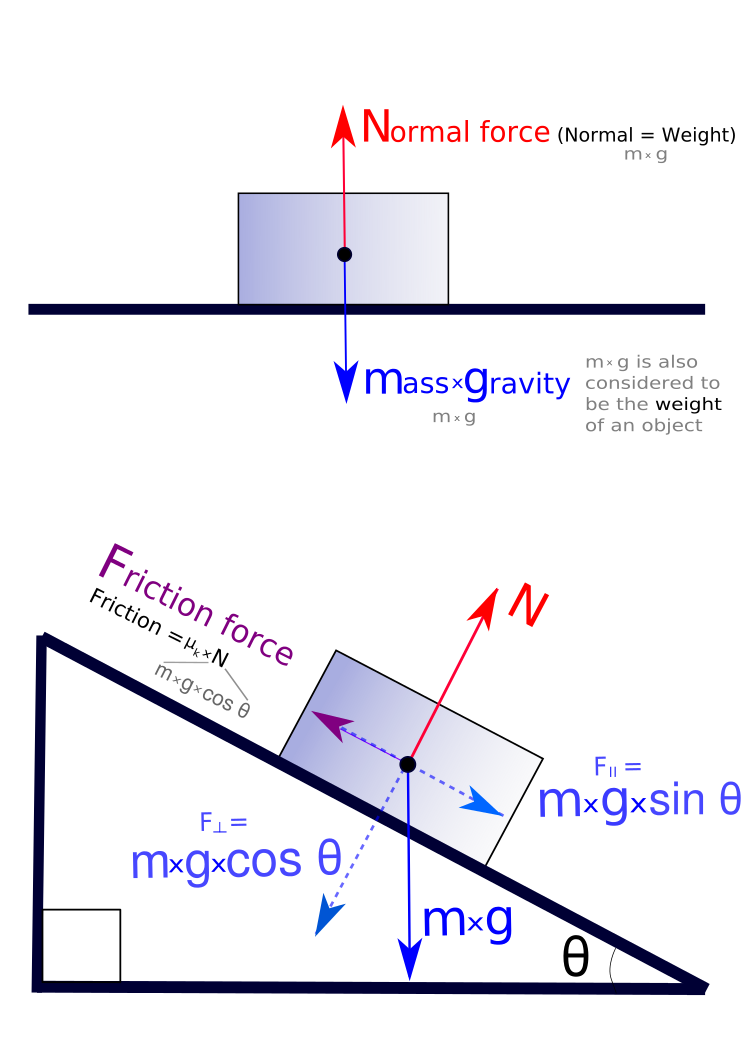
Forces as Vectors: Free-body diagrams of an object on a flat surface and an inclined plane. Forces are resolved and added together to determine their magnitudes and the net force.
Key Points
- When determining what happens when two forces act on the same object, it is necessary to know both the magnitude and the direction of both forces to calculate the result.
- When two forces act on a point particle, the resulting force or the resultant (also called the net force ), can be determined by following the parallelogram rule of vector addition.
- Free-body diagrams can be used as a convenient way to keep track of forces acting on an object.
Key Terms
- vector: A directed quantity, one with both magnitude and direction; the between two points.
- free-body diagram: A free body diagram, also called a force diagram, is a pictorial representation often used by physicists and engineers to analyze the forces acting on a body of interest.
- resultant: A vector that is the vector sum of multiple vectors
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Net force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Net_force. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Force. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14040/latest/. License: CC BY: Attribution
- Force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Force. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42069/latest/?collection=col11406/1.7. License: CC BY: Attribution
- resultant. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/resultant. License: CC BY-SA: Attribution-ShareAlike
- vector. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/vector. License: CC BY-SA: Attribution-ShareAlike
- free-body diagram. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/free-body%20diagram. License: CC BY-SA: Attribution-ShareAlike
- File:Freebodydiagram3 pn.svg - Wikipedia, the free encyclopedia. Provided by: Wikipedia. Located at: en.Wikipedia.org/w/index.php?title=File:Freebodydiagram3_pn.svg&page=1. License: CC BY-SA: Attribution-ShareAlike

