5.3: Velocity, Acceleration, and Force
- Last updated
- Save as PDF
- Page ID
- 16949

- Boundless
- Boundless
Rotational Angle and Angular Velocity
The rotational angle is a measure of how far an object rotates, and angular velocity measures how fast it rotates.
learning objectives
- Express the relationship between the rotational angle and the distance
Rotational Angle and Angular Velocity
When an object rotates about an axis, as with a tire on a car or a record on a turntable, the motion can be described in two ways. A point on the edge of the rotating object will have some velocity and will be carried through an arc by riding the spinning object. The point will travel through a distance of \(\mathrm{ΔS}\), but it is often more convenient to talk about the extent the object has rotated. The amount the object rotates is called the rotational angle and may be measured in either degrees or radians. Since the rotational angle is related to the distance \(\mathrm{ΔS}\) and to the radius \(\mathrm{r}\) by the equation \(\mathrm{Δθ=\frac{ΔS}{R}}\), it is usually more convenient to use radians.
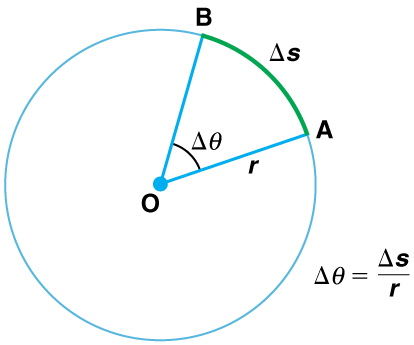
Angle θ and Arc Length s: The radius of a circle is rotated through an angle \(\mathrm{Δθ}\). The arc length \(\mathrm{Δs}\) is described on the circumference.
The speed at which the object rotates is given by the angular velocity, which is the rate of change of the rotational angle with respect to time. Although the angle itself is not a vector quantity, the angular velocity is a vector. The direction of the angular velocity vector is perpendicular to the plane of rotation, in a direction which is usually specified by the right-hand rule. Angular acceleration gives the rate of change of angular velocity. The angle, angular velocity, and angular acceleration are very useful in describing the rotational motion of an object.
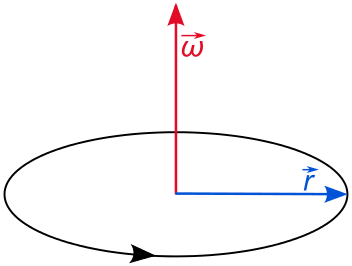
The Direction of Angular Velocity: The angular velocity describes the speed of rotation and the orientation of the instantaneous axis about which the rotation occurs. The direction of the angular velocity will be along the axis of rotation. In this case (counter-clockwise rotation), the vector points upwards.
When the axis of rotation is perpendicular to the position vector, the angular velocity may be calculated by taking the linear velocity \(\mathrm{v}\) of a point on the edge of the rotating object and dividing by the radius. This will give the angular velocity, usually denoted by \(\mathrm{ω}\), in terms of radians per second.
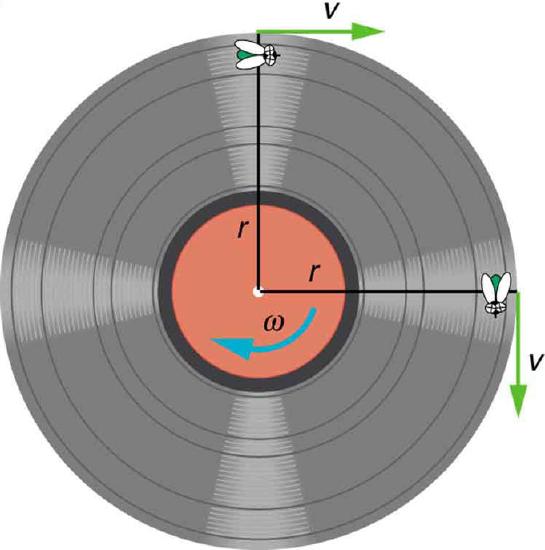
Angular Velocity: A fly on the edge of a rotating object records a constant velocity \(\mathrm{v}\). The object is rotating with an angular velocity equal to \(\mathrm{\frac{v}{r}}\).
Centripetial Acceleration
Centripetal acceleration is the constant change in velocity necessary for an object to maintain a circular path.
learning objectives
- Express the centripetal acceleration in terms of rotational velocity
Overview
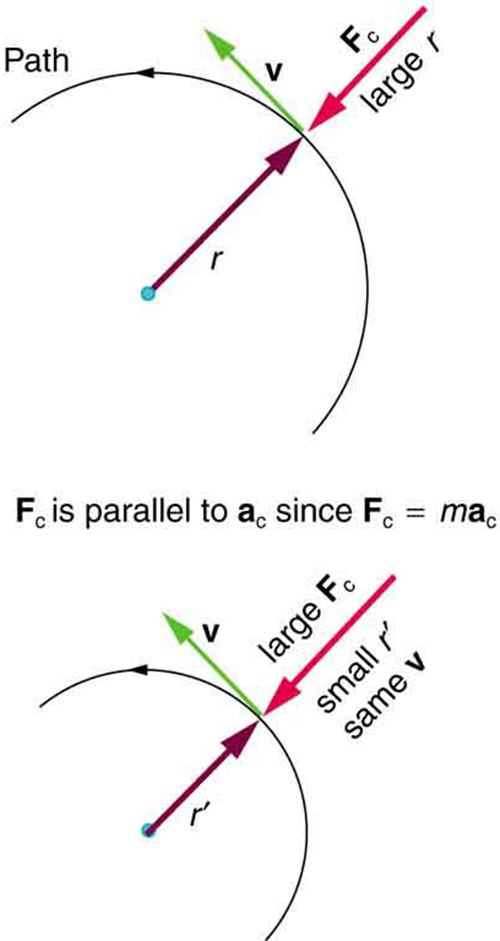
As mentioned in previous sections on kinematics, any change in velocity is given by an acceleration. Often the changes in velocity are changes in magnitude. When an object speeds up or slows down this is a change in the objects velocity. Changes in the magnitude of the velocity match our intuitive and every day usage of the term accelerate. However, because velocity is a vector, it also has a direction. Therefore, any change in the direction of travel of an object must also be met with an acceleration.
Uniform circular motion involves an object traveling a circular path at constant speed. Since the speed is constant, one would not usually think that the object is accelerating. However, the direction is constantly changing as the object traverses the circle. Thus, it is said to be accelerating. One can feel this acceleration when one is on a roller coaster. Even if the speed is constant, a quick turn will provoke a feeling of force on the rider. This feeling is an acceleration.
Centripetal Acceleration: A brief overview of centripetal acceleration for high school physics students.
Calculating Centripetal Acceleration
To calculate the centripetal acceleration of an object undergoing uniform circular motion, it is necessary to have the speed at which the object is traveling and the radius of the circle about which the motion is taking place. The simple equation is:
\[\mathrm{a_c=\dfrac{v^2}{r}}\]
where \(\mathrm{v}\) is the linear velocity of the object and \(\mathrm{r}\) is the radius of the circle.
The centripetal acceleration may also be expressed in terms of rotational velocity as follows:
\[\mathrm{a_c=ω^2r}\]
with omega being the rotational velocity given by \(\mathrm{\frac{v}{r}}\).

Centripetal Acceleration: As an object moves around a circle, the direction of the velocity vector constantly changes.
Centripetal Force
A force which causes motion in a curved path is called a centripetal force (uniform circular motion is an example of centripetal force).
learning objectives
- Express the equations for the centripetal force and acceleration
A force that causes motion in a curved path is called a centripetal force. Uniform circular motion is an example of centripetal force in action. It can be seen in the orbit of satellites around the earth, the tension in a rope in a game of tether ball, a roller coaster loop de loop, or in a bucket swung around the body.
Overview of centripetal force: A brief overview of centripetal force.
Previously, we learned that any change in a velocity is an acceleration. As the object moves through the circular path it is constantly changing direction, and therefore accelerating—causing constant force to be acting on the object. This centripetal force acts toward the center of curvature, toward the axis of rotation. Because the object is moving perpendicular to the force, the path followed by the object is a circular one. It is this force that keeps a ball from falling out of a bucket if you swing it in circular continuously.
Centripetal force: As an object travels around a circular path at a constant speed, it experiences a centripetal force accelerating it toward the center.
The equation for centripetal force is as follows:
\[\mathrm{Fc=\dfrac{mv^2}{r}}\]
where: \(\mathrm{F_c}\) is centripetal force, \(\mathrm{m}\) is mass, \(\mathrm{v}\) is velocity, and \(\mathrm{r}\) is the radius of the path of motion.
From Newton’s second law \(\mathrm{F=m⋅a}\), we can see that centripetal acceleration is:
\[\mathrm{a_c=\dfrac{v^2}{r}}\]
Centripetal force can also be expressed in terms of angular velocity. Angular velocity is the measure of how fast an object is traversing the circular path. As the object travels its path, it sweeps out an arc that can be measured in degrees or radians. The equation for centripetal force using angular velocity is:
\[\mathrm{F_c=mrω^2}\]
Key Points
- When an object rotates about an axis, the points on the edge of the object travel in arcs.
- The angle these arcs sweep out is called the rotational angle, and it is usually represented by the symbol theta.
- A measure of how quickly the object is rotating, with respect to time, is called the angular velocity. It is usually represented by a Greek omega symbol. Like its counterpart linear velocity, it is a vector.
- For an object to maintain circular motion it must constantly change direction.
- Since velocity is a vector, changes in direction constitute changes in velocity.
- A change in velocity is known as an acceleration. The change in velocity due to circular motion is known as centripetal acceleration.
- Centripetal acceleration can be calculated by taking the linear velocity squared divided by the radius of the circle the object is traveling along.
- When an object is in uniform circular motion, it is constantly changing direction, and therefore accelerating. This is angular acceleration.
- A force acting on the object in uniform circular motion (called centripetal force) is acting on the object from the center of the circle.
Key Terms
- radians: The angle subtended at the centre of a circle by an arc of the circle of the same length as the circle’s radius.
- acceleration: The amount by which a speed or velocity increases (and so a scalar quantity or a vector quantity).
- circular motion: Motion in such a way that the path taken is that of a circle.
- velocity: A vector quantity that denotes the rate of change of position with respect to time, or a speed with a directional component.
- centripetal: Directed or moving towards a center.
- angular velocity: A vector quantity describing an object in circular motion; its magnitude is equal to the speed of the particle and the direction is perpendicular to the plane of its circular motion.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- OpenStax College, Rotation Angle and Angular Velocity. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/. License: CC BY: Attribution
- radians. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/radians. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, Rotation Angle and Angular Velocity. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg. License: CC BY: Attribution
- Angular velocity. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Angular_velocity. License: CC BY: Attribution
- OpenStax College, Centripetal Acceleration. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42084/latest/. License: CC BY: Attribution
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/circular-motion. License: CC BY-SA: Attribution-ShareAlike
- velocity. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/velocity. License: CC BY-SA: Attribution-ShareAlike
- acceleration. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/acceleration. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, Rotation Angle and Angular Velocity. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg. License: CC BY: Attribution
- Angular velocity. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Angular_velocity. License: CC BY: Attribution
- Centripetal Acceleration. Located at: http://www.youtube.com/watch?v=EX5DZ2MHlV4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Centripetal Acceleration. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg. License: CC BY: Attribution
- OpenStax College, Centripetal Force. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42086/latest/. License: CC BY: Attribution
- centripetal. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/centripetal. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/angular-velocity. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, Rotation Angle and Angular Velocity. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg. License: CC BY: Attribution
- Angular velocity. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Angular_velocity. License: CC BY: Attribution
- Centripetal Acceleration. Located at: http://www.youtube.com/watch?v=EX5DZ2MHlV4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Centripetal Acceleration. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg. License: CC BY: Attribution
- OpenStax College, Centripetal Force. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42086/latest/Figure_07_03_01a.jpg. License: CC BY: Attribution
- Overview of centripetal force. Located at: http://www.youtube.com/watch?v=ldQWTNDBSSE. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license

