learning objectives
- Assess the relationship between radians the the revolution of a CD
When objects rotate about some axis—for example, when the CD (compact disc) rotates about its center—each point in the object follows a circular arc. Consider a line from the center of the CD to its edge. Each pit used to record sound along this line moves through the same angle in the same amount of time. The rotation angle is the amount of rotation, and is analogous to linear distance. We define the rotation angle \(\mathrm{Δθ}\) to be the ratio of the arc length to the radius of curvature:
\(\mathrm{Δθ=\frac{Δs}{r}}\) (illustrated in ).
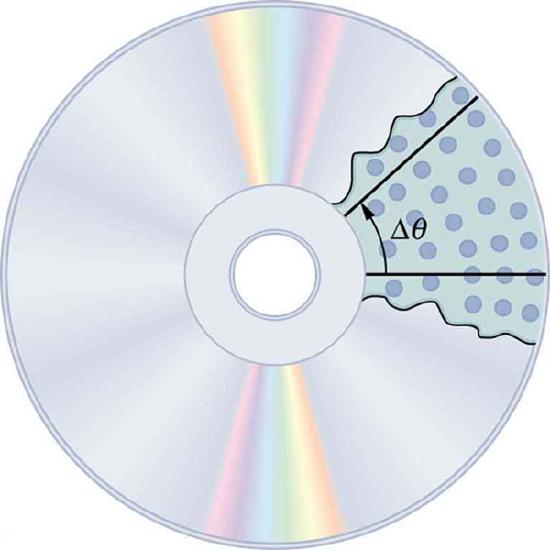
Rotation Angle: All points on a CD travel in circular arcs. The pits along a line from the center to the edge all move through the same angle Δ in a time Δt.
In mathematics, the angle of rotation (or angular position ) is a measurement of the amount (i.e., the angle) that a figure is rotated about a fixed point (often the center of a circle, as shown in ).
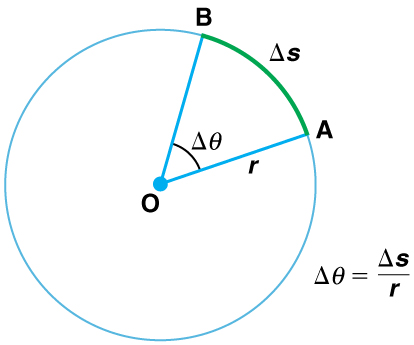
Angle θ and Arc Length s: The radius of a circle is rotated through an angle Δ. The arc length Δs is described on the circumference.
The arc length Δs is the distance traveled along a circular path. r is the radius of curvature of the circular path. We know that for one complete revolution, the arc length is the circumference of a circle of radius r. The circumference of a circle is 2πr. Thus, for one complete revolution the rotation angle is:
\[\mathrm{Δθ=\dfrac{(2πr)}{r}=2π.}\]
This result is the basis for defining the units used to measure rotation angles to be radians (rad), defined so that:
\[\mathrm{2π \; rad = 1 \; revolution.}\]
If \(\mathrm{Δθ = 2π \; rad}\), then the CD has made one complete revolution, and every point on the CD is back at its original position. Because there are 360º in a circle or one revolution, the relationship between radians and degrees is thus \(\mathrm{2π \; rad=360º}\), so that:
\[\mathrm{1 \; rad = \dfrac{360º}{2π} = 57.3º.}\]
Angular Velocity, Omega
Angular velocity ω is the rate of change of an angle, mathematically defined as \(\mathrm{ω = \frac{Δθ}{Δt}}\).
learning objectives
- Examine how fast an object is rotating based on angular velocity
To examine how fast an object is rotating, we define angular velocity ω as the rate of change of an angle. In symbols, this is
\[\mathrm{ω=\dfrac{Δθ}{Δt},}\]
where an angular rotation Δ takes place in a time Δt. The greater the rotation angle in a given amount of time, the greater the angular velocity. The units for angular velocity are radians per second (rad/s).
Angular velocity ω is analogous to linear velocity v. To find the precise relationship between angular and linear velocity, we again consider a pit on the rotating CD. This pit moves an arc length Δs in a time Δt, and so it has a linear velocity \(\mathrm{v = \frac{Δs}{Δt}}\).
From \(\mathrm{Δθ=\frac{(Δs)}{r}}\) we see that \(\mathrm{Δs=r \cdot Δθ}\). Substituting this into the expression for v gives \(\mathrm{v=\frac{(r \cdot Δθ)}{(Δt)}=r(\frac{Δθ}{Δt})=rω.}\)
We can write this relationship in two different ways: \(\mathrm{v=rω}\) or \(\mathrm{ω=\frac{v}{r}}\).
The first relationship states that the linear velocity v is proportional to the distance from the center of rotation, thus it is largest for a point on the rim (largest r), as you might expect. We can also call this linear speed v of a point on the rim the tangential speed. The second relationship can be illustrated by considering the tire of a moving car, as shown in the picture below. Note that the speed of the point at the center of the tire is the same as the speed v of the car. The faster the car moves, the faster the tire spins—large v means a large ω, because v=rω. Similarly, a larger-radius tire rotating at the same angular velocity (ω) will produce a greater linear speed (v) for the car.
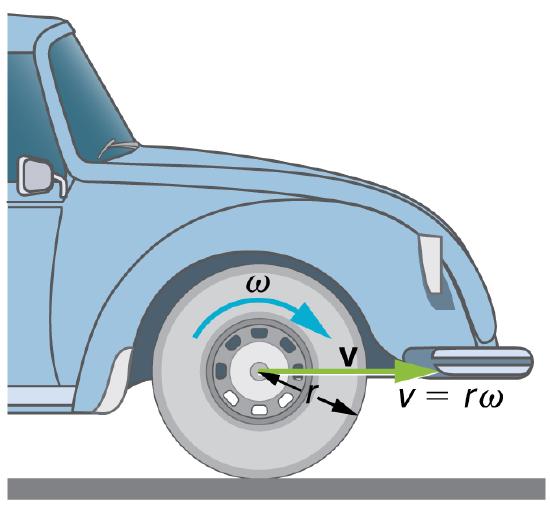
Angular Velocity: A car moving at a velocity v to the right has a tire rotating with an angular velocity ω. The speed of the tread of the tire relative to the axle is v, the same as if the car were jacked up. Thus the car moves forward at linear velocity v=rω, where r is the tire radius. A larger angular velocity for the tire means a greater velocity for the car.
Angular Acceleration, Alpha
Angular acceleration is the rate of change of angular velocity, expressed mathematically as \(\mathrm{α=\frac{Δω}{Δt}}\).
learning objectives
- Explain the relationship between angular acceleration and angular velocity
Angular acceleration is the rate of change of angular velocity. In SI units, it is measured in radians per second squared (rad/s2), and is usually denoted by the Greek letter alpha (\(\mathrm{α}\)).
Consider the following situations in which angular velocity is not constant: when a skater pulls in her arms, when a child starts up a merry-go-round from rest, or when a computer’s hard disk slows to a halt when switched off. In all these cases, there is an angular acceleration in which ωω changes. The faster the change occurs, the greater the angular acceleration. Angular acceleration is defined as the rate of change of angular velocity. In equation form, angular acceleration is expressed as follows:
\[\mathrm{α=\dfrac{Δω}{Δt}}\]
where \(\mathrm{Δω}\) is the change in angular velocity and \(\mathrm{Δt}\) is the change in time. The units of angular acceleration are (rad/s)/s, or rad/s2. If ωω increases, then αα is positive. If ωω decreases, then αα is negative.
It is useful to know how linear and angular acceleration are related. In circular motion, there is acceleration that is tangent to the circle at the point of interest (as seen in the diagram below). This acceleration is called tangential acceleration, at.
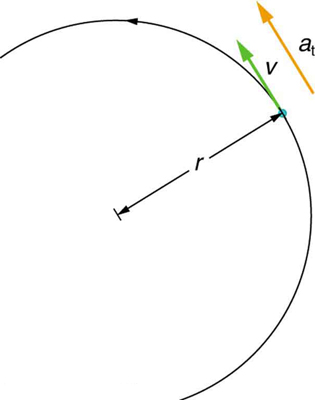
Tangential acceleration: In circular motion, acceleration can occur as the magnitude of the velocity changes: a is tangent to the motion. This acceleration is called tangential acceleration.
Tangential acceleration refers to changes in the magnitude of velocity but not its direction. In circular motion, centripetal acceleration, ac, refers to changes in the direction of the velocity but not its magnitude. An object undergoing circular motion experiences centripetal acceleration (as seen in the diagram below.) Thus, at and ac are perpendicular and independent of one another. Tangential acceleration at is directly related to the angular acceleration and is linked to an increase or decrease in the velocity (but not its direction).
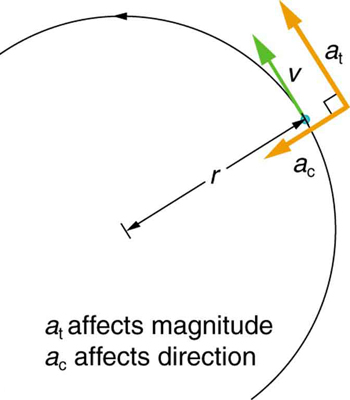
Centripetal Acceleration: Centripetal acceleration occurs as the direction of velocity changes; it is perpendicular to the circular motion. Centripetal and tangential acceleration are thus perpendicular to each other.
Key Points
- The arc length Δs is the distance traveled along a circular path. r is the radius of curvature of the circular path.
- The rotation angle is the amount of rotation and is analogous to linear distance. We define the rotation angle \(\mathrm{Δθ}\) to be the ratio of the arc length to the radius of curvature: \(\mathrm{Δθ = \frac{Δs}{r}}\).
- For one complete revolution the rotation angle is 2π.
- The greater the rotation angle in a given amount of time, the greater the angular velocity.
- Angular velocity ω is analogous to linear velocity v.
- We can write the relationship between linear velocity and angular velocity in two different ways: \(\mathrm{v=rω}\) or \(\mathrm{ω=\frac{v}{r}}\).
- The faster the change in angular velocity occurs, the greater the angular acceleration.
- In circular motion, linear acceleration is tangent to the circle at the point of interest, and is called tangential acceleration.
- In circular motion, centripetal acceleration refers to changes in the direction of the velocity but not its magnitude. An object undergoing circular motion experiences centripetal acceleration.
Key Terms
- Angular position: The angle in radians (degrees, revolutions) through which a point or line has been rotated in a specified sense about a specified axis.
- angular velocity: A vector quantity describing an object in circular motion; its magnitude is equal to the speed of the particle and the direction is perpendicular to the plane of its circular motion.
- angular acceleration: The rate of change of angular velocity, often represented by α.
- tangential acceleration: The acceleration in a direction tangent to the circle at the point of interest in circular motion.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Angle of rotation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Angle_of_rotation. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Angular position. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Angular%20position. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/angular-velocity. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42177/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Angular acceleration. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Angular_acceleration. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/tangential-acceleration. License: CC BY-SA: Attribution-ShareAlike
- angular acceleration. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/angular_acceleration. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42177/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. November 10, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42177/latest/?collection=col11406/1.7. License: CC BY: Attribution







