10.2: Density and Pressure
- Last updated
- Jan 14, 2019
- Save as PDF
- Page ID
- 16993

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Identify factors that determine the pressure exerted by the gas
Pressure is an important physical quantity—it plays an essential role in topics ranging from thermodynamics to solid and fluid mechanics. As a scalar physical quantity (having magnitude but no direction), pressure is defined as the force per unit area applied perpendicular to the surface to which it is applied. Pressure can be expressed in a number of units depending on the context of use.
Pressure and Pascal’s Principle: A brief introduction to pressure and Pascal’s Principle, including hydraulics.
Units, Equations and Representations
In SI units, the unit of pressure is the Pascal (Pa), which is equal to a Newton / meter2 (N/m2). Other important units of pressure include the pound per square inch (psi) and the standard atmosphere (atm). The elementary mathematical expression for pressure is given by:
pressure=ForceArea=FA
where p is pressure, F is the force acting perpendicular to the surface to which this force is applied, and A is the area of the surface. Any object that possesses weight, whether at rest or not, exerts a pressure upon the surface with which it is in contact. The magnitude of the pressure exerted by an object on a given surface is equal to its weight acting in the direction perpendicular to that surface, divided by the total surface area of contact between the object and the surface. shows the graphical representations and corresponding mathematical expressions for the case in which a force acts perpendicular to the surface of contact, as well as the case in which a force acts at angle θ relative to the surface.
Representation of Pressure: This image shows the graphical representations and corresponding mathematical expressions for the case in which a force acts perpendicular to the surface of contact, as well as the case in which a force acts at angle θ relative to the surface.
Pressure as a Function of Surface Area
Since pressure depends only on the force acting perpendicular to the surface upon which it is applied, only the force component perpendicular to the surface contributes to the pressure exerted by that force on that surface. Pressure can be increased by either increasing the force or by decreasing the area or can oppositely be decreased by either decreasing the force or increasing the area. illustrates this concept. A rectangular block weighing 1000 N is first placed horizontally. It has an area of contact (with the surface upon which it is resting) of 0.1 m2, thus exerting a pressure of 1,000 Pa on that surface. That same block in a different configuration (also in Figure 2), in which the block is placed vertically, has an area of contact with the surface upon which it is resting of 0.01 m2, thus exerting a pressure of 10,000 Pa—10 times larger than the first configuration due to a decrease in the surface area by a factor of 10.
Pressure as a Function of Surface Area: Pressure can be increased by either increasing the force or by decreasing the area or can oppositely be decreased by either decreasing the force or increasing the area.
A good illustration of this is the reason a sharp knife is far more effective for cutting than a blunt knife. The same force applied by a sharp knife with a smaller area of contact will exert a much greater pressure than a blunt knife having a considerably larger area of contact. Similarly, a person standing on one leg on a trampoline causes a greater displacement of the trampoline than that same person standing on the same trampoline using two legs—not because the individual exerts a larger force when standing on one leg, but because the area upon which this force is exerted is decreased, thus increasing the pressure on the trampoline. Alternatively, an object having a weight larger than another object of the same dimensionality and area of contact with a given surface will exert a greater pressure on that surface due to an increase in force. Finally, when considering a given force of constant magnitude acting on a constant area of a given surface, the pressure exerted by that force on that surface will be greater the larger the angle of that force as it acts upon the surface, reaching a maximum when that force acts perpendicular to the surface.
Liquids and Gases: Fluids
Just as a solid exerts a pressure on a surface upon which it is in contact, liquids and gases likewise exert pressures on surfaces and objects upon which they are in contact with. The pressure exerted by an ideal gas on a closed container in which it is confined is best analyzed on a molecular level. Gas molecules in a gas container move in a random manner throughout the volume of the container, exerting a force on the container walls upon collision. Taking the overall average force of all the collisions of the gas molecules confined within the container over a unit time allows for a proper measurement of the effective force of the gas molecules on the container walls. Given that the container acts as a confining surface for this net force, the gas molecules exert a pressure on the container. For such an ideal gas confined within a rigid container, the pressure exerted by the gas molecules can be calculated using the ideal gas law:
p=nRTV
where n is the number of gas molecules, R is the ideal gas constant (R = 8.314 J mol-1 K-1), T is the temperature of the gas, and V is the volume of the container.
The pressure exerted by the gas can be increased by: increasing the number of collisions of gas molecules per unit time by increasing the number of gas molecules; increasing the kinetic energy of the gas by increasing the temperature; or decreasing the volume of the container. offers a representation of the ideal gas law, as well as the effect of varying the equation parameters on the gas pressure. Another common type of pressure is that exerted by a static liquid or hydrostatic pressure. Hydrostatic pressure is most easily addressed by treating the liquid as a continuous distribution of matter, and may be considered a measure of energy per unit volume or energy density. We will further discuss hydrostatic pressure in other sections.
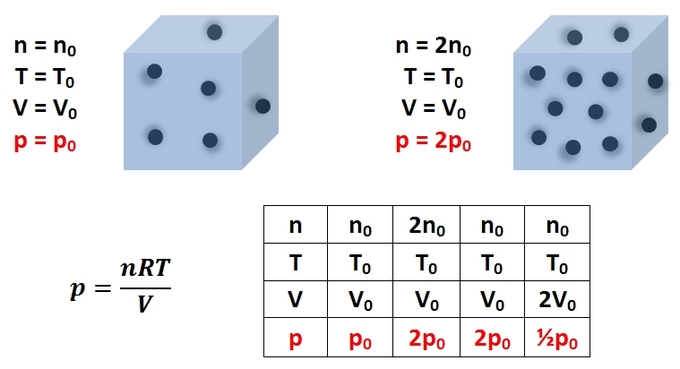
Pressure of an Ideal Gas: This image is a representation of the ideal gas law, as well as the effect of varying the equation parameters on the gas pressure.
Variation of Pressure With Depth
Pressure within static fluids depends on the properties of the fluid, the acceleration due to gravity, and the depth within the fluid.
learning obectives
- Identify factors that determine the pressure exerted by static liquids and gases
Pressure is defined in simplest terms as force per unit area. However, when dealing with pressures exerted by gases and liquids, it is most convenient to approach pressure as a measure of energy per unit volume by means of the definition of work (W = F·d). The derivation of pressure as a measure of energy per unit volume from its definition as force per unit area is given in. Since, for gases and liquids, the force acting on a system contributing to pressure does not act on a specific point or particular surface, but rather as a distribution of force, analyzing pressure as a measure of energy per unit volume is more appropriate. For liquids and gases at rest, the pressure of the liquid or gas at any point within the medium is called the hydrostatic pressure. At any such point within a medium, the pressure is the same in all directions, as if the pressure was not the same in all directions, the fluid, whether it is a gas or liquid, would not be static. Note that the following discussion and expressions pertain only to incompressible fluids at static equilibrium.
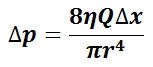
Energy per Unit Volume: This equation is the derivation of pressure as a measure of energy per unit volume from its definition as force per unit area.
The pressure exerted by a static liquid depends only on the depth, density of the liquid, and the acceleration due to gravity. gives the expression for pressure as a function of depth within an incompressible, static liquid as well as the derivation of this equation from the definition of pressure as a measure of energy per unit volume (ρ is the density of the gas, g is the acceleration due to gravity, and h is the depth within the liquid). For any given liquid with constant density throughout, pressure increases with increasing depth. For example, a person under water at a depth of h1 will experience half the pressure as a person under water at a depth of h2=2h1. For many liquids, the density can be assumed to be nearly constant throughout the volume of the liquid and, for virtually all practical applications, so can the acceleration due to gravity (g = 9.81 m/s2). As a result, pressure within a liquid is therefore a function of depth only, with the pressure increasing at a linear rate with respect to increasing depth. In practical applications involving calculation of pressure as a function of depth, an important distinction must be made as to whether the absolute or relative pressure within a liquid is desired. Equation 2 by itself gives the pressure exerted by a liquid relative to atmospheric pressure, yet if the absolute pressure is desired, the atmospheric pressure must then be added to the pressure exerted by the liquid alone.
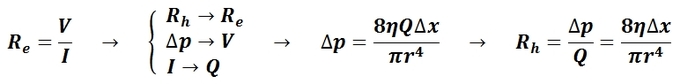
Pressure as Energy per Unit Volume: This equation gives the expression for pressure as a function of depth within an incompressible, static liquid as well as the derivation of this equation from the definition of pressure as a measure of energy per unit volume (ρ is the density of the gas, g is the acceleration due to gravity, and h is the depth within the liquid).
When analyzing pressure within gases, a slightly different approach must be taken as, by the nature of gases, the force contributing to pressure arises from the average number of gas molecules occupying a certain point within the gas per unit time. Thus the force contributing to the pressure of a gas within the medium is not a continuous distribution as for liquids and the barometric equation given in must be utilized to determine the pressure exerted by the gas at a certain depth (or height) within the gas (p0 is the pressure at h = 0, M is the mass of a single molecule of gas, g is the acceleration due to gravity, k is the Boltzmann constant, T is the temperature of the gas, and h is the height or depth within the gas). Equation 3 assumes that the gas is incompressible and that the pressure is hydrostatic.
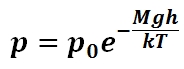
Pressure within a gas: The force contributing to the pressure of a gas within the medium is not a continuous distribution as for liquids and the barometric equation given in this figure must be utilized to determine the pressure exerted by the gas at a certain depth (or height) within the gas (p0 is the pressure at h = 0, M is the mass of a single molecule of gas, g is the acceleration due to gravity, k is the Boltzmann constant, T is the temperature of the gas, and h is the height or depth within the gas)
Static Equilibrium
Any region or point, or any static object within a static fluid is in static equilibrium where all forces and torques are equal to zero.
learning obectives
- Identify required conditions for a fluid to be in rest
Static equilibrium is a particular state of a physical system. It is qualitatively described by an object at rest and by the sum of all forces, with the sum of all torques acting on that object being equal to zero. Static objects are in static equilibrium, with the net force and net torque acting on that object being equal to zero; otherwise there would be a driving mechanism for that object to undergo movement in space. The analysis and study of objects in static equilibrium and the forces and torques acting on them is called statics—a subtopic of mechanics. Statics is particularly important in the design of static and load bearing structures. As it pertains to fluidics, static equilibrium concerns the forces acting on a static object within a fluid medium.
Fluids
For a fluid at rest, the conditions for static equilibrium must be met at any point within the fluid medium. Therefore, the sum of the forces and torques at any point within the static liquid or gas must be zero. Similarly, the sum of the forces and torques of an object at rest within a static fluid medium must also be zero. In considering a stationary object within a liquid medium at rest, the forces acting at any point in time and at any point in space within the medium must be analyzed. For a stationary object within a static liquid, there are no torques acting on the object so the sum of the torques for such a system is immediately zero; it need not concern analysis since the torque condition for equilibrium is fulfilled.
Density
At any point in space within a static fluid, the sum of the acting forces must be zero; otherwise the condition for static equilibrium would not be met. In analyzing such a simple system, consider a rectangular region within the fluid medium with density ρL (same density as the fluid medium), width w, length l, and height h, as shown in. Next, the forces acting on this region within the medium are taken into account. First, the region has a force of gravity acting downwards (its weight) equal to its density object, times its volume of the object, times the acceleration due to gravity. The downward force acting on this region due to the fluid above the region is equal to the pressure times the area of contact. Similarly, there is an upward force acting on this region due to the fluid below the region equal to the pressure times the area of contact. For static equilibrium to be achieved, the sum of these forces must be zero, as shown in. Thus for any region within a fluid, in order to achieve static equilibrium, the pressure from the fluid below the region must be greater than the pressure from the fluid above by the weight of the region. This force which counteracts the weight of a region or object within a static fluid is called the buoyant force (or buoyancy).
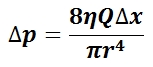
Static Equilibrium of a Region Within a Fluid: This figure shows the equations for static equilibrium of a region within a fluid.
Region Within a Static Fluid: This figure is a free body diagram of a region within a static fluid.
In the case on an object at stationary equilibrium within a static fluid, the sum of the forces acting on that object must be zero. As previously discussed, there are two downward acting forces, one being the weight of the object and the other being the force exerted by the pressure from the fluid above the object. At the same time, there is an upwards force exerted by the pressure from the fluid below the object, which includes the buoyant force. shows how the calculation of the forces acting on a stationary object within a static fluid would change from those presented in if an object having a density ρS different from that of the fluid medium is surrounded by the fluid. The appearance of a buoyant force in static fluids is due to the fact that pressure within the fluid changes as depth changes. The analysis presented above can furthermore be extended to much more complicated systems involving complex objects and diverse materials.
Pascal’s Principle
Pascal’s Principle states that pressure is transmitted and undiminished in a closed static fluid.
learning obectives
- Apply Pascal’s Principle to describe pressure behavior in static fluids
Pascal’s Principle
Pascal’s Principle (or Pascal’s Law ) applies to static fluids and takes advantage of the height dependency of pressure in static fluids. Named after French mathematician Blaise Pascal, who established this important relationship, Pascal’s Principle can be used to exploit pressure of a static liquid as a measure of energy per unit volume to perform work in applications such as hydraulic presses. Qualitatively, Pascal’s Principle states that pressure is transmitted undiminished in an enclosed static liquid. Quantitatively, Pascal’s Law is derived from the expression for determining the pressure at a given height (or depth) within a fluid and is defined by Pascal’s Principle:
Pressure and Pascal’s Principle: A brief introduction to pressure and Pascal’s Principle, including hydraulics.
p2=p1+Δp,Δp=ρgΔh
where p1 is the external applied pressure, ρ is the density of the fluid, Δh is the difference in height of the static liquid, and g is the acceleration due to gravity. Pascal’s Law explicitly determines the pressure difference between two different heights (or depths) within a static liquid. As, by Pascal’s Law, a change in pressure is linearly proportional to a change in height within an incompressible, static liquid of constant density, doubling the height between the two points of reference will double the change of pressure, while halving the height between the two points will half the change in pressure.
Enclosed Static Liquids
While Pascal’s Principle applies to any static fluid, it is most useful in terms of applications when considering systems involving rigid wall closed column configurations containing homogeneous fluids of constant density. By exploiting the fact that pressure is transmitted undiminished in an enclosed static liquid, such as in this type of system, static liquids can be used to transform small amounts of force into large amounts of force for many applications such as hydraulic presses.
As an example, referring to, a downwards force of 10 N is applied to a bottle filled with a static liquid of constant density ρ at the spout of cross-sectional area of 5 cm2, yielding an applied pressure of 2 N/cm2. The cross-sectional area of the bottle changes with height so that at the bottom of the bottle the cross-sectional area is 500 cm2. As a result of Pascal’s Law, the pressure change (pressure applied to the static liquid) is transmitted undiminished in the static liquid so that the applied pressure is 2 N/m2 at the bottom of the bottle as well. Furthermore, the hydrostatic pressure due to the difference in height of the liquid is given by Equation 1 and yields the total pressure at the bottom surface of the bottle. Since the cross-sectional area at the bottom of the bottle is 100 times larger than at the top, the force contributing to the pressure at the bottom of the bottle is 1000 N plus the force from the weight of the static fluid in the bottle. This example shows how, through Pascal’s Principle, the force exerted by a static fluid in a closed system can be multiplied by changing the height and the surface area of contact.
Pressure Applied to a Hydrostatic Fluid: A downwards force of 10 N is applied to a bottle filled with a static liquid of constant density ρ at the spout of cross-sectional area of 5 cm2, yielding an applied pressure of 2 N/cm2.
Pressure Transmitted Throughout an Entire Fluid
As stated by Pascal’s Principle, the pressure applied to a static fluid in a closed container is transmitted throughout the entire fluid. Taking advantage of this phenomenon, hydraulic presses are able to exert a large amount of force requiring a much smaller amount of input force. This gives two different types of hydraulic press configurations, the first in which there is no difference in height of the static liquid and the second in which there is a difference in height Δh of the static liquid. In the first configuration, a force F1 is applied to a static liquid of density ρ across a surface area of contact A1, yielding an input pressure of P2. On the other side of the press configuration, the fluid exerts an output pressure P1 across a surface area of contact A2, where A2 > A1. By Pascal’s Principle, P1 = P2, yielding a force exerted by the static fluid of F2, where F2 > F1. Depending on the applied pressure and geometry of the hydraulic press, the magnitude of F2 can be changed. In the second configuration, the geometry of the system is the same, except that the height of the fluid on the output end is a height Δh less than the height of the fluid at the input end. The difference in height of the fluid between the input and the output ends contributes to the total force exerted by the fluid. For a hydraulic press, the force multiplication factor is the ratio of the output to the input contact areas.
Hydraulic Press Diagrams: Two different types of hydraulic press configurations, the first in which there is no difference in height of the static liquid and the second in which there is a difference in height Δh of the static liquid.
Gauge Pressure and Atmospheric Pressure
Pressure is often measured as gauge pressure, which is defined as the absolute pressure minus the atmospheric pressure.
learning obectives
- Explain the relationship among absolute pressure, gauge pressure, and atmospheric pressure
Atmospheric Pressure
An important distinction must be made as to the type of pressure quantity being used when dealing with pressure measurements and calculations. Atmospheric pressure is the magnitude of pressure in a system due to the atmosphere, such as the pressure exerted by air molecules (a static fluid ) on the surface of the earth at a given elevation. In most measurements and calculations, the atmospheric pressure is considered to be constant at 1 atm or 101,325 Pa, which is the atmospheric pressure under standard conditions at sea level.
Atmospheric pressure is due to the force of the molecules in the atmosphere and is a case of hydrostatic pressure. Depending on the altitude relative to sea level, the actual atmospheric pressure will be less at higher altitudes and more at lower altitudes as the weight of air molecules in the immediate atmosphere changes, thus changing the effective atmospheric pressure. Atmospheric pressure is a measure of absolute pressure and can be affected by the temperature and air composition of the atmosphere but can generally be accurately approximated to be around standard atmospheric pressure of 101,325 Pa. Within the majority of earth’s atmosphere, pressure varies with height according to. In this equation p0 is the pressure at sea level (101,325 Pa), g is the acceleration due to gravity, M is the mass of a single molecule of air, R is the universal gas constant, T0 is the standard temperature at sea level, and h is the height relative to sea level.
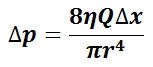
Pressure and Height: Atmospheric pressure depends on altitude or height.
Gauge Pressure
For most applications, particularly those involving pressure measurements, it is more practical to use gauge pressure than absolute pressure as a unit of measurement. Gauge pressure is a relative pressure measurement which measures pressure relative to atmospheric pressure and is defined as the absolute pressure minus the atmospheric pressure. Most pressure measuring equipment give the pressure of a system in terms of gauge pressure as opposed to absolute pressure. For example, tire pressure and blood pressure are gauge pressures by convention, while atmospheric pressures, deep vacuum pressures, and altimeter pressures must be absolute.
For most working fluids where a fluid exists in a closed system, gauge pressure measurement prevails. Pressure instruments connected to the system will indicate pressures relative to the current atmospheric pressure. The situation changes when extreme vacuum pressures are measured; absolute pressures are typically used instead.
To find the absolute pressure of a system, the atmospheric pressure must then be added to the gauge pressure. While gauge pressure is very useful in practical pressure measurements, most calculations involving pressure, such as the ideal gas law, require pressure values in terms of absolute pressures and thus require gauge pressures to be converted to absolute pressures.
Measurements: Gauge Pressure and the Barometer
Barometers are devices used for measuring atmospheric and gauge pressure indirectly through the use of hydrostatic fluids.
learning obectives
- Compare design and operation of aneroid and hydrostatic based barometers
Gauge Pressure
In practice, pressure is most often measured in terms of gauge pressure. Gauge pressure is the pressure of a system above atmospheric pressure. Since atmospheric pressure is mostly constant with little variation near sea level, where most practical pressure measurements are taken, it is assumed to be approximately 101,325 Pa. Modern pressure measuring devices sometimes have incorporated mechanisms to account for changes in atmospheric pressure due to elevation changes. Gauge pressure is much more convenient than absolute pressure for practical measurements and is widely used as an established measure of pressure. However, it is important to determine whether it is necessary to use absolute (gauge plus atmospheric) pressure for calculations, as is often the case for most calculations, such as those involving the ideal gas law. Pressure measurements have been accurately taken since the mid-1600s with the invention of the traditional barometer. Barometers are devices used to measure pressure and were initially used to measure atmospheric pressure.
Hydrostatic Based Barometers
Early barometers were used to measure atmospheric pressure through the use of hydrostatic fluids. Hydrostatic based barometers consist of columnar devices usually made from glass and filled with a static liquid of consistent density. The columnar section is sealed, holds a vacuum, and is partially filled with the liquid while the base section is open to the atmosphere and makes an interface with the surrounding environment. As the atmospheric pressure changes, the pressure exerted by the atmosphere on the fluid reservoir exposed to the atmosphere at the base changes, increasing as the atmospheric pressure increases and decreasing as the atmospheric pressure decreases. This change in pressure causes the height of the fluid in the columnar structure to change, increasing in height as the atmosphere exerts greater pressure on the liquid in the reservoir base and decreasing as the atmosphere exerts lower pressure on the liquid in the reservoir base. The height of the liquid within the glass column then gives a measure of the atmospheric pressure. Pressure, as determined by hydrostatic barometers, is often measured by determining the height of the liquid in the barometer column, thus the torr as a unit of pressure, but can be used to determine pressure in SI units. Hydrostatic based barometers most commonly use water or mercury as the static liquid. While the use of water is much less hazardous than mercury, mercury is often a better choice for fabricating accurate hydrostatic barometers. The density of mercury is much higher than that of water, thus allowing for higher accuracy of measurements and the ability to fabricate more compact hydrostatic barometers. In theory, a hydrostatic barometer can be placed in a closed system to measure the absolute pressure and the gauge pressure of the system by subtracting the atmospheric pressure.
Aneroid Barometer
Another type of barometer is the aneroid barometer, which consists of a small, flexible sealed metal box called an aneroid cell. The aneroid cell is made from beryllium-copper alloy and is partially evacuated. A stiff spring prevents the aneroid cell from collapsing. Small changes in external air pressure cause the cell to expand or contract. This expansion and contraction is amplified by mechanical mechanisms to give a pressure reading. Such pressure measuring devices are more practical than hydrostatic barometers for measuring system pressures. Many modern pressure measuring devices are pre-engineered to output gauge pressure measurements. While the aneroid barometer is the underlying mechanism behind many modern pressure measuring devices, pressure can also be measured using more advanced measuring mechanisms.
Hydrostatic Column Barometer: The concept of determining pressure using the fluid height in a hydrostatic column barometer
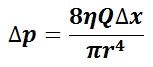
Variation of Pressure with Height: The density of the liquid is p, g is the acceleration due to gravity, and h is the height of the fluid in the barometer column.
Pressure in the Body
Pressure plays an essential role in a number of critical bodily functions including respiration and blood circulation.
learning obectives
- Explain role played by pressure in the circulatory and respiratory systems
The Role of Pressure in the Circulatory System
Pressure plays an essential role in various critical bodily systems that are necessary for survival. One such critical bodily system which relies on pressure for functionality is the circulatory system, which is an example of a closed fluid system under pressure. The circulatory system is responsible for transporting oxygen and essential nutrients to all organs within the body as well as removing waste materials from these organs. Blood can be regarded as a viscous liquid contained within the circulatory system that travels throughout this closed system as a result of pressure and pressure differences within the circulatory system.
As the volume of blood within the circulatory system is confined to the veins, arteries, and capillaries there is a pressure within this closed system. Furthermore, through a complicated system of veins, arteries, and capillaries of varying diameter as well as valves and the heart acting as a continuous pump, pressure differences arise within the circulatory system that result in the potential for blood to circulate throughout the circulatory system, thus carrying out essential bodily functions for survival.
Pressure within the circulatory system is referred to as blood pressure, and is a primary and crucial vital sign which can be used to diagnose or indicate a number of medical conditions. Blood pressure varies throughout the body as well as from one individual to another and depends on a number of factors such as heart rate, blood volume, resistance of the circulatory system (veins, arteries, and capillaries), and the viscosity of blood. Any medical conditions affecting any of these factors will have an effect on blood pressure and the overall health of the circulatory system.
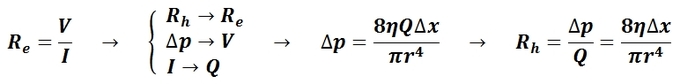
Approximation for Mean Arterial Pressure: In practice, the mean arterial pressure (MAP) can be approximated from easily obtainable blood pressure measurements.
The mean arterial pressure (MAP) is the average pressure over a cardiac cycle and is determined by, where CO is the cardiac outputs, SVR is the systemic vascular resistance, and CVP is the central venous pressure (CVP). In practice, the mean arterial pressure (MAP) can be approximated from easily obtainable blood pressure measurements in, where Psys is the measured systolic pressure and Pdias is the measured diastolic pressure. One particularly common and dangerous circulatory system condition is partial blockage of blood vessels due to a number of factors, such as plaque build-up from high cholesterol, which results in a reduction of the effective blood vessel cross-sectional diameter and a corresponding reduction in blood flow rate and thus an increase in blood pressure to restore normal blood flow according to Poiseuille’s Law.
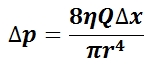
Equation for Mean Arterial Pressure: The mean arterial pressure (MAP) is the average pressure over a cardiac cycle and is determined this equation, where CO is the cardiac outputs, SVR is the systemic vascular resistance, and CVP is the central venous pressure (CVP).
The Role of Pressure in the Respiratory System
Pressure also plays an essential role in the respiratory system, as it is responsible for the breathing mechanism. Pressure differences between the lungs and the atmosphere create a potential for air to enter the lungs, resulting in inhalation. The mechanism resulting in inhalation is due to lowering of the diaphragm, which increases the volume of the thoracic cavity surrounding the lungs, thus lowering its pressure as determined by the ideal gas law. The reduction in pressure of the thoracic cavity, which normally has a negative gauge pressure, thus keeping the lungs inflated, pulls air into the lungs, inflating the alveoli and resulting in oxygen transport needed for respiration. As the diaphragm restores and moves upwards, pressure within the thoracic cavity increases, resulting in exhalation. The cycle repeats itself, resulting in the respiration which as discussed is mechanically due to pressure changes. Without pressure in the body, and the corresponding potential that it has for dynamic bodily processes, essential functions such as blood circulation and respiration would not be possible.
Key Points
- Pressure is a scalar quantity defined as force per unit area. Pressure only concerns the force component perpendicular to the surface upon which it acts, thus if the force acts at an angle, the force component along the direction perpendicular to the surface must be used to calculate pressure.
- The pressure exerted on a surface by an object increases as the weight of the object increases or the surface area of contact decreases. Alternatively the pressure exerted decreases as the weight of the object decreases or the surface area of contact increases.
- Pressure exerted by ideal gases in confined containers is due to the average number of collisions of gas molecules with the container walls per unit time. As such, pressure depends on the amount of gas (in number of molecules), its temperature, and the volume of the container.
- Hydrostatic pressure refers to the pressure exerted by a fluid (gas or liquid) at any point in space within that fluid, assuming that the fluid is incompressible and at rest.
- Pressure within a liquid depends only on the density of the liquid, the acceleration due to gravity, and the depth within the liquid. The pressure exerted by such a static liquid increases linearly with increasing depth.
- Pressure within a gas depends on the temperature of the gas, the mass of a single molecule of the gas, the acceleration due to gravity, and the height (or depth) within the gas.
- Hydrostatic balance is the term used for a region or stationary object within a static fluid which is at static equilibrium, and for which the sum of all forces and sum of all torques is equal to zero.
- A region or static object within a stationary fluid experiences downward forces due to the weight of the region or object, and the pressure exerted from the fluid above the region or object, as well as an upward force due to the pressure exerted from the fluid below the region or object.
- For a region or static object within a static fluid, the downward force due to the weight of the region or object is counteracted by the upward buoyant force, which is equal to the weight of the fluid displaced by the region or object.
- Pascal’s Principle is used to quantitatively relate the pressure at two points in an incompressible, static fluid. It states that pressure is transmitted, undiminished, in a closed static fluid.
- The total pressure at any point within an incompressible, static fluid is equal to the sum of the applied pressure at any point in that fluid and the hydrostatic pressure change due to a difference in height within that fluid.
- Through the application of Pascal’s Principle, a static liquid can be utilized to generate a large output force using a much smaller input force, yielding important devices such as hydraulic presses.
- Atmospheric pressure is a measure of absolute pressure and is due to the weight of the air molecules above a certain height relative to sea level, increasing with decreasing altitude and decreasing with increasing altitude.
- Gauge pressure is the additional pressure in a system relative to atmospheric pressure. It is a convenient pressure measurement for most practical applications.
- While gauge pressure is more convenient for practical measurements, absolute pressure is necessary for most pressure calculations, thus the atmospheric pressure must be added to the gauge pressure for calculations.
- Gauge pressure is the pressure of a system above atmospheric pressure, which must be converted to absolute pressure for most calculations.
- The barometer is a device which uses hydrostatic fluids to directly determine atmospheric pressure and may be used to indirectly measure the gauge pressure of systems.
- The hydrostatic column barometer uses a liquid like water or mercury for functionality, while the aneroid barometer uses an evacuated flexible metal cell.
- Pressure, along with the potential for work arising from differences in pressure, plays an essential role in the functionality of several critical bodily functions and systems necessary for survival.
- The circulatory system relies on pressure differences for circulating blood, along with oxygen, necessary nutrients, and waste products throughout the body.
- Respiration is made possible as a result of pressure differences between the thoracic cavity, the lungs, and the environment and is largely regulated by movement of the diaphragm.
Key Terms
- ideal gas: Theoretical gas characterized by random motion whose individual molecules do not interact with one another and are chemically inert.
- kinetic energy: The energy associated with a moving particle or object having a certain mass.
- incompressible: Unable to be compressed or condensed.
- static equilibrium: the physical state in which all components of a system are at rest and the net force is equal to zero throughout the system
- Buoyancy: The power of supporting a body so that it floats; upward pressure exerted by the fluid in which a body is immersed.
- torque: Something that produces or tends to produce torsion or rotation; the moment of a force or system of forces tending to cause rotation.
- equilibrium: A state of rest or balance due to the equal action of opposing forces.
- hydraulic press: Device that uses a hydraulic cylinder (closed static fluid) to generate a compressive force.
- Gauge Pressure: The pressure of a system above atmospheric pressure.
- Torr: A unit of pressure equal to one millimeter of mercury (760 torr = 101,325 Pa).
- Aneroid Barometer: A device for measuring pressure, often specially calibrated for use as an altimeter, consisting of a box or chamber partially exhausted of air, having an elastic top and a pointer to indicate the degree of compression of the top caused by the external air.
- Thoracic Cavity: A hollow place or space, or a potential space, within the body or one of its organs.
- Poiseuille’s Law: The law that the velocity of a liquid flowing through a capillary is directly proportional to the pressure of the liquid and the fourth power of the radius of the capillary and is inversely proportional to the viscosity of the liquid and the length of the capillary.
- Alveoli: Small air sacs or cavities in the lung that give the tissue a honeycomb appearance and expand its surface area for the exchange of oxygen and carbon dioxide.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- ideal gas. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/ideal_gas. License: CC BY-SA: Attribution-ShareAlike
- Pressure. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Pressure. License: CC BY-SA: Attribution-ShareAlike
- kinetic energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/kinetic%20energy. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pressure and Pascal's Principle. Located at: http://www.youtube.com/watch?v=MK_cG85iOO4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Fluid statics. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Fluid_statics%23Pressure_in_fluids_at_rest. License: CC BY-SA: Attribution-ShareAlike
- Pressure. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Pressure. License: CC BY-SA: Attribution-ShareAlike
- incompressible. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/incompressible. License: CC BY-SA: Attribution-ShareAlike
- static equilibrium. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/static_equilibrium. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pressure and Pascal's Principle. Located at: http://www.youtube.com/watch?v=MK_cG85iOO4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Mechanical equilibrium. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Mechanical_equilibrium. License: CC BY-SA: Attribution-ShareAlike
- Hydrostatic equilibrium). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Hydrostatic_equilibrium). License: CC BY-SA: Attribution-ShareAlike
- torque. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/torque. License: CC BY-SA: Attribution-ShareAlike
- equilibrium. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/equilibrium. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pressure and Pascal's Principle. Located at: http://www.youtube.com/watch?v=MK_cG85iOO4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pascal's law. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Pascal's_law. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pressure and Pascal's Principle. Located at: http://www.youtube.com/watch?v=MK_cG85iOO4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pressure and Pascal's Principle. Located at: http://www.youtube.com/watch?v=MK_cG85iOO4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Pressure measurement. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Pressure_measurement. License: CC BY-SA: Attribution-ShareAlike
- Atmospheric pressure. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Atmospheric_pressure. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pressure and Pascal's Principle. Located at: http://www.youtube.com/watch?v=MK_cG85iOO4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pressure and Pascal's Principle. Located at: http://www.youtube.com/watch?v=MK_cG85iOO4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: N/A. Located at: N/A. License: Public Domain: No Known Copyright
- Pressure measurement. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Pressure_measurement. License: CC BY-SA: Attribution-ShareAlike
- Barometer. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Barometer. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pressure and Pascal's Principle. Located at: http://www.youtube.com/watch?v=MK_cG85iOO4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pressure and Pascal's Principle. Located at: http://www.youtube.com/watch?v=MK_cG85iOO4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: N/A. Located at: N/A. License: Public Domain: No Known Copyright
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/poiseuille-s-law--3. License: CC BY-SA: Attribution-ShareAlike
- Blood pressure. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Blood_pressure. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/alveoli--2. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/thoracic-cavity. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pressure and Pascal's Principle. Located at: http://www.youtube.com/watch?v=MK_cG85iOO4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Pressure and Pascal's Principle. Located at: http://www.youtube.com/watch?v=MK_cG85iOO4. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: N/A. Located at: N/A. License: Public Domain: No Known Copyright
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike


