1.4: Damped and Driven Oscillations
- Last updated
- Jan 15, 2019
- Save as PDF
- Page ID
- 17095

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Describe the time evolution of the motion of the damped harmonic oscillator
The Physical Situation
The simple harmonic oscillator describes many physical systems throughout the world, but early studies of physics usually only consider ideal situations that do not involve friction. In the real world, however, frictional forces – such as air resistance – will slow, or dampen, the motion of an object. Sometimes, these dampening forces are strong enough to return an object to equilibrium over time.
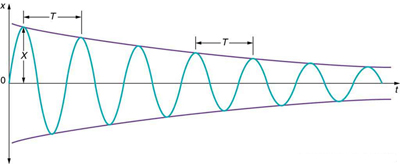
Damped Harmonic Motion: Illustrating the position against time of our object moving in simple harmonic motion. We see that for small damping, the amplitude of our motion slowly decreases over time.
The simplest and most commonly seen case occurs when the frictional force is proportional to an object’s velocity. Note that other cases exist which may lead to nonlinear equations which go beyond the scope of this example.
Consider an object of mass m attached to a spring of constant k. Let the damping force be proportional to the mass’ velocity by a proportionality constant, b, called the vicious damping coefficient. We can describe this situation using Newton’s second law, which leads to a second order, linear, homogeneous, ordinary differential equation. We simply add a term describing the damping force to our already familiar equation describing a simple harmonic oscillator to describe the general case of damped harmonic motion.
Fnet=md2xdt2+bdxdt+kx=0=d2xdt2+bmdxdt+kmx=0=d2xdt2+γdxdt+ω20x=0
ω20=km,γ=bm
This notation usesd2xdt2, the acceleration of our object, dxdt, the velocity of our object, ω0, undamped angular frequency of oscillation, and ɣ, which we can call the damping ratio.
Solving the Differential Equation; Interpreting Results
We solve this differential equation for our equation of motion of the system, x(t). We assume a solution in the form of an exponential, where a is a constant value which we will solve for.
x(t)=eat
Plugging this into the differential equation we find that there are three results for a, which will dictate the motion of our system. We can solve for a by using the quadratic equation.
Fnet=a2x+γax+ω20x=0=a2+γa+ω20=0
a=γ±√γ2−4ω202
The physical situation has three possible results depending on the value of a, which depends on the value of what is under our radical. This expression can be positive, negative, or equal to zero which will result in overdamping, underdamping, and critical damping, respectively.
γ2>4ω20 is the Over Damped case. In this case, the system returns to equilibrium by exponentially decaying towards zero. The system will not pass the equilibrium position more than once.
γ2<4ω20 is the Under Damped case. In this case, the system oscillates as it slowly returns to equilibrium and the amplitude decreases over time. Figure 1 depicts an underdamped case.
γ2=4ω20 is theCritically Damped case. In this case, the system returns to equilibrium very quickly without oscillating and without passing the equilibrium position at all.
Driven Oscillations and Resonance
Driven harmonic oscillators are damped oscillators further affected by an externally applied force.
learning objectives
- Describe a driven harmonic oscillator as a type of damped oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, xF→=−k→x where k is a positive constant. If a frictional force ( damping ) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator.
Driven harmonic oscillators are damped oscillators further affected by an externally applied force F(t). Newton’s second law takes the form F(t)−kx−cdxdt=md2xdt2. It is usually rewritten into the form d2xdt2+2ζω0dxdt+ω20x=F(t)m. This equation can be solved exactly for any driving force, using the solutions z(t) which satisfy the unforced equation: d2zdt2+2ζω0dzdt+ω20z=0, and which can be expressed as damped sinusoidal oscillationsz(t)=Ae−ζω0tsin(√1−ζ2ω0t+φ)in the case where ζ≤1. The amplitude A and phase φ determine the behavior needed to match the initial conditions. In the case ζ<1 and a unit step input with x(0)=0 the solution is: x(t)=1−e−ζω0tsin(√1−ζ2ω0t+φ)sin(φ)with phase φ given by cosφ=ζ. The time an oscillator needs to adapt to changed external conditions is of the order \(\mathrm{τ =\frac{1}{(ζ_0)}}\). In physics, the adaptation is called relaxation, and τ is called the relaxation time.
In the case of a sinusoidal driving force: d2xdt2+2ζω0dxdt+ω20x=1mF0sin(ωt), where F0 is the driving amplitude and ωω is the driving frequency for a sinusoidal driving mechanism. This type of system appears in AC driven RLC circuits (resistor-inductor-capacitor) and driven spring systems having internal mechanical resistance or external air resistance. The general solution is a sum of a transient solution that depends on initial conditions, and a steady state that is independent of initial conditions and depends only on the driving amplitude F0, driving frequency ωω, undamped angular frequency ω0, and the damping ratio ζ. For a particular driving frequency called the resonance, or resonant frequency ωr=ω0√1−2ζ2, the amplitude (for a given F0) is maximum. This resonance effect only occurs when ζ<1/√2, i.e. for significantly underdamped systems. For strongly underdamped systems the value of the amplitude can become quite large near the resonance frequency (see ).
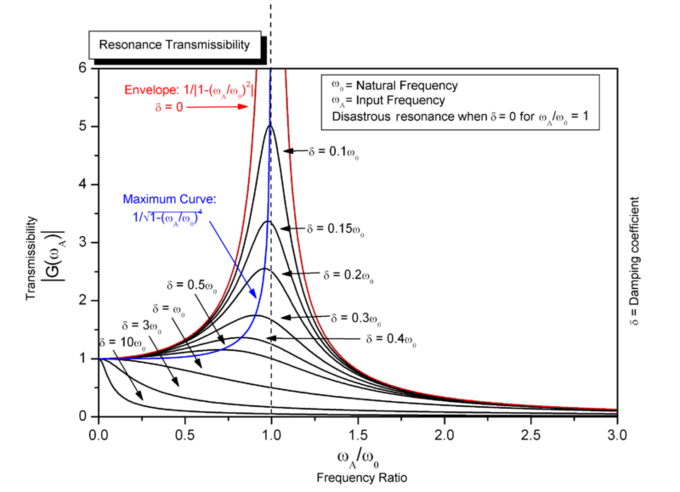
Resonance: Steady state variation of amplitude with frequency and damping of a driven simple harmonic oscillator.
Key Points
- To describe a damped harmonic oscillator, add a velocity dependent term, bx, where b is the vicious dampingcoefficient.
- Solve the differential equation for the equation of motion, x(t).
- Depending on the values of the damping coefficient and undamped angular frequency, the results will be one of three cases: an under damped system, an over damped system, or a critically damped system.
- Newton’s second law takes the form F(t)−kx−cdxdt=md2xdt2for driven harmonic oscillators.
- The resonance effect occurs only in the underdamped systems.
- For strongly underdamped systems the value of the amplitude can become quite large near the resonance frequency.
Key Terms
- Under Damped: “The condition in which damping of an oscillator causes it to return to equilibrium with the amplitude gradually decreasing to zero; system returns to equilibrium faster but overshoots and crosses the equilibrium position one or more times. “
- Critically Damped: “The condition in which the damping of an oscillator causes it to return as quickly as possible to its equilibrium position without oscillating back and forth about this position. “
- Over Damped: “The condition in which damping of an oscillator causes it to return to equilibrium without oscillating; oscillator moves more slowly toward equilibrium than in the critically damped system. “
- oscillator: A pattern that returns to its original state, in the same orientation and position, after a finite number of generations.
- equilibrium: The state of a body at rest or in uniform motion, the resultant of all forces on which is zero.
- force: A physical quantity that denotes ability to push, pull, twist or accelerate a body which is measured in a unit dimensioned in mass × distance/time² (ML/T²): SI: newton (N); CGS: dyne (dyn)
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/under-damped. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/over-damped. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/critically-damped. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Damped Harmonic Motion. November 3, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42246/latest/. License: CC BY: Attribution
- Driven oscillations. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Driven_oscillations%23Driven_harmonic_oscillators. License: CC BY-SA: Attribution-ShareAlike
- equilibrium. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/equilibrium. License: CC BY-SA: Attribution-ShareAlike
- oscillator. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/oscillator. License: CC BY-SA: Attribution-ShareAlike
- force. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/force. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Damped Harmonic Motion. November 3, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42246/latest/. License: CC BY: Attribution
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/0/07/Resonance.PNG/800px-Resonance.PNG. License: CC BY-SA: Attribution-ShareAlike

