3.5: Inside the Black Hole
( \newcommand{\kernel}{\mathrm{null}\,}\)
The previous section looked at local inertial reference frames in the vicinity of a black hole, which we could use to determine speed as a function of the r-coordinate. We found that as an object approaches the event horizon, it's speed approaches the speed of light. Things break down, however, if r<2M because the LIRF energy becomes imaginary and the object's speed exceeds the speed of light. This actually happens because it is not possible to construct an LIRF inside of a black hole.
To see what happens inside of a black hole, we need to use a metric other than the Schwarzschild metric since the Schwarzschild metric has problems at r=2M. There is actually another spherically symmetric solution to the Einstein Field Equations called the Global Rain metric. The word "rain" is a reference to the fact that the T-coordinate is measured by steadily infalling clocks. The Global Rain spacetime interval is given by the following.
dτ2=(1−2Mr)dT2−2√2MrdT dr−dr2−r2dθ2−r2sin2θdϕ2=(dTdrdθdϕ)(1−2Mr2√2Mr002√2Mr10000r20000r2sin2θ)(dTdrdθdϕ)
The r-, θ, and ϕ-coordinates are the same as before, but now we have T instead of t. Notice also that we have an off-diagonal term in the metric. While that may seem weird, it is perfectly allowable. Just don't think too much about what it means.
Argue that the global rain metric is spherically symmetric and reduces to flat spacetime in the appropriate limits.
- Answer
-
The metric is spherically symmetric because the metric components depend only on r and not θ or ϕ. In the limits M→0 and r→∞, we get
dτ2=dT2−dr2−r2dθ2−r2sin2dϕ2,
which is a flat metric in spherical coordinates.
We can see what the light cones look like by setting dτ=0 in Equation 3.5.1. The result is shown in Fig. 3.5.1.
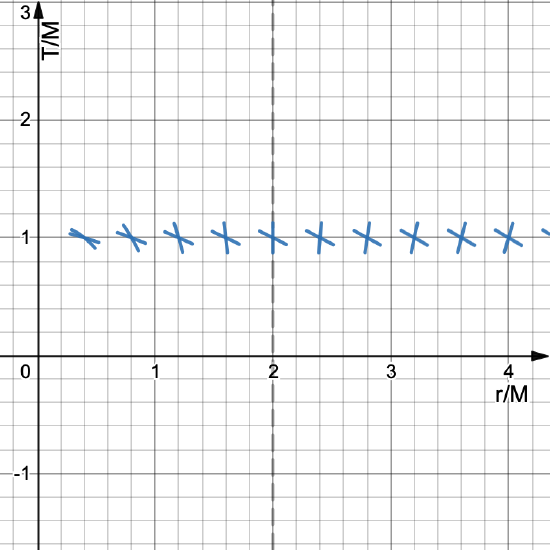
As shown in Fig. 3.5.1, the light cones are similar to those of flat spacetime far away from the black hole. The closer you get to the center, more the light cone tilts to the left.
According to Fig. 3.5.1, is the event horizon a barrier to motion in global rain coordinates?
- Answer
-
In Schwarzschild coordinates, we saw that light cones squeezed infinitely the closer you got to the event horizon, which indicated that for particles just outside the event horizon, there was no future inside. Here, however, we see no such squeezing. Particles just outside the event horizon do have a possible future within the event horizon.
What this indicates is that the problems that we saw at r=2M are simply due to the particular coordinate system we were using, similar to how the instruction "walk north" stops making sense once you get to the north pole. It's not that the north pole is an actual barrier, it's that the instruction stops making sense given how we define the word "north."
At any particular point inside a black hole, you can draw one ingoing worldline of light and one "outgoing" worldline of light. Why did I put "outgoing" in quotation marks?
- Answer
-
As you can see inside the black hole, there are no worldlines of light that move to larger values of r. This means that even light is not fast enough to escape. The rules of geometry inside of a black hole are so messed up that every direction is inward.
Show that dτ2=dT2−(dr+√2MrdT)2−r2dθ2−r2sin2θdϕ2 is equivalent to Equation 3.5.1.
Show that the slopes of the worldlines of light in global rain coordinates are given by dTdr=1−√2Mr±1.


