4.1: Membrane Permeability
( \newcommand{\kernel}{\mathrm{null}\,}\)
Cells are the main units of organization in biology. All cells are contained by a cell membrane (biomembrane) selectively open to some chemicals and ions but acts as a barrier to undesired components [1]. To put it another way, biomembranes are enclosing membranes which function as selectively permeable barriers to chemicals and ions. It should be noted though that the title biomembrane may denote a wide range of definitions; especially, cellular membranes should not be confused with isolating tissues formed by layers of cells (e.g., mucous membranes). Here the focus would be on biological membranes in the form of cell membranes, often consist of a phospholipid bilayer with embedded, integral, and/or peripheral proteins responsible for communication and transportation of chemicals and ions.
Selectivity of Biomembranes
When a membrane separates two aqueous compartments, some chemicals can move across the membrane while others cannot. This behavior can be seen with pure synthetic phospholipid membranes, which are practically biomembranes with no protein. Membrane proteins play a crucial role as transporters in expediting the ions and chemical transfers across the cell membranes. Based on the transport mechanism and permeability, solutes can be divided into three main groups as follows [2]:
- Small lipophilic (lipid soluble) molecules that transfer through the membrane by the sole diffusion.
- Molecules that cross the membrane with the aid of protein channels.
- Very large molecules that do not cross the membrane at all.
Schematic cartoon given by Figure 4.1.1 can clearly illustrate the selective permeability of biomembranes for different solutes. A few lipophilic substances move freely across the cell membrane by passive diffusion. Lipophilicity is a measure for the tendency of a compound to partition into nonpolar (organic) solvent (versus aqueous solvent). Most small molecules/ions need the assistance of specific protein channels to transport them through the cell membrane. These inside-out protein channels are called transporters. Finally, the very large molecules do not cross the membrane, except in certain special cases.
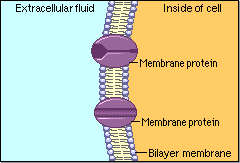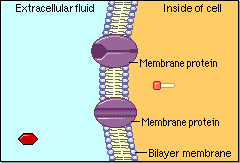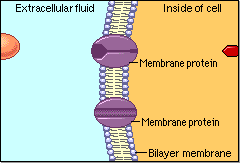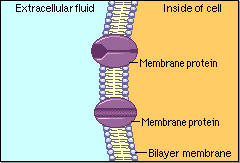
Generally speaking, two different classes of membrane transports can be considered [3]:
- Rapid, stereo-selective protein-mediated transport
- Slow, non-specific diffusion of molecules across cell membrane
It is worth noting that the mediated transport can be used in drug delivery and defects in transport are the causes of many diseases.
Small Lipophilic Molecules (Passive Diffusion)
Certain substances easily pass through the membrane by passive diffusion. Examples of chemicals that passively diffuse across the cell membranes are gases, like O2 and CO2, and small relatively hydrophobic molecules, such as fatty acids and alcohols. Logarithm of octanol/water partition coefficient of the solute (Ko/w) can be a measure of lipophilicity (higher the log(Ko/w), higher the lipophilicity of the solute will be). However, larger lipophilicity values should not be always interpreted as better passive diffusion. The underlying reason is that there are two counter-effect parameters: besides being lipid-soluble (to cross the membrane), the solute should also possess enough water solubility to dissolve in the body fluids. Usually, a compound with log(Ko/w) > 5 is too hydrophobic to passively diffuse through the biological membranes.
In contrast to small lipophilic molecules, in absence of protein channels, it is difficult for water to pass through the pure phospholipid membranes via diffusion. Moreover, almost all polar and charged molecules such as sugars, amino acids, and ions completely fail to cross the pure phospholipid membranes.
Polar and Charged Molecules (Protein-Mediated Transfer)
Biological membranes are permeable not only to gases and small lipophilic molecules (by passive diffusion processes), but also to many polar and charged molecules, including water, but through a different path. There are many different proteins located in biomembranes with the main function of effectively transporting certain solutes across the membrane. According to their functions, there are two main groups of transport proteins: channel proteins and carrier proteins. Channel proteins promote the transfer of water molecules and certain ions by forming hydrophilic pores, while carrier proteins bind to specific solutes and carry them across the membrane [2]. All in all, whether it is of channel or carrier type, protein functions as an enzyme expediting the transfer of polar and charged molecules. All channel proteins and some carrier proteins facilitate the transfer of chemical/ions downhill respected to the concentration gradient, a process known as facilitated diffusion. Facilitated diffusion requires no energy input, in contrast to active transport processes (solute transport against the concentration gradient) that require an external source energy [2].
Large Molecules (Membrane Barriers)
Very large molecules like proteins, polysaccharides or nucleic acids, do not diffuse across the cell membranes at all. They can pass through the membrane only when broken down into their component monomers (e.g., amino acids, sugars, or nucleotides).
Passive and Active Transport
Most biologically important solutes require protein carriers to cross cell membranes, by a process of either passive or active transport. Active transport requires the cell to expend energy to move the materials, while passive transport can be done without using cellular energy [4]. To put it another way, active transport uses energy to move a solute "uphill" against its gradient, whereas in facilitated diffusion, a solute moves down its concentration gradient and no energy input is required.
Therefore, to summarize, transport of solutes across cell membranes by protein carriers can occur in one of two ways [2]:
- Downhill movement of solutes from regions of higher to lower concentration level, with the assistance of the protein carrier to pass through the membrane. This process is called passive transport or facilitated diffusion, and does not require energy.
- Uphill movement of solute against the concentration gradient driving force (from regions of lower to higher concentration). Based on the chemical driving force, this process is unfavorable and requires some form of chemical energy to occur (active transport).
The type of transport process, facilitated/active transport, a biological cell employs is strictly dependent on its specific needs and concentration level of chemical/ions. For example, red blood cells use facilitated diffusion to transfer glucose across membranes, whereas intestinal epithelial cells rely on active transport to take in glucose from the gut [2]. Facilitated diffusion is effective for red blood cells primarily because the glucose concentration in the blood is stable and higher than the cellular level. In contrast, active transport is needed for the gut since there are large fluctuations of glucose level as a result of eating.
Figure 4.1.2 encapsulates different transfer mechanisms discussed so far. Please note that the concentration gradient driving force is assumed downward in this schematic diagram.
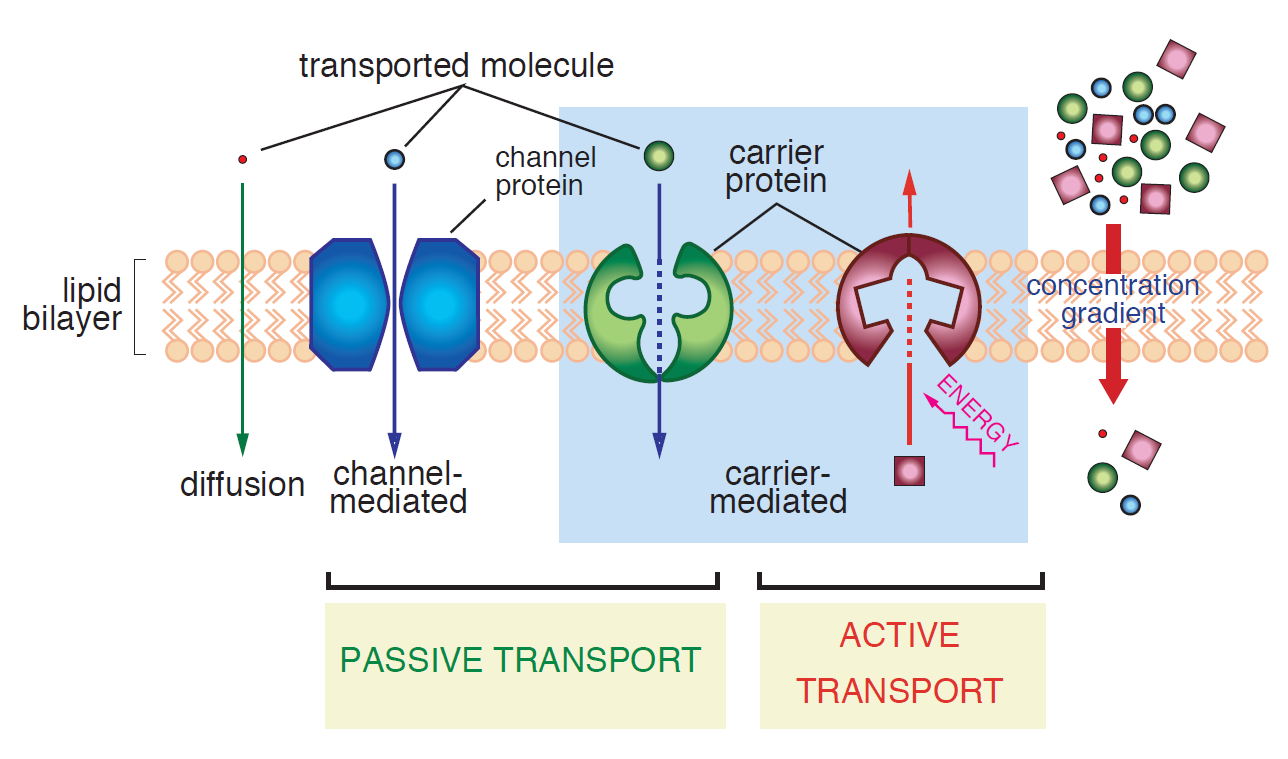
Facilitated Diffusion
In principle, there are two types of facilitated diffusion carriers as follows:
- Water molecules or certain ions can be transported by channel proteins. By forming a protein-lined pathway across the membrane, proteins can appreciably speed up the transfer rate of such solutes. It should be noted though that each type of channel protein is very selective to a specific ion/chemical. For example, some channels allow only K+ ions to pass whereas they act like a barrier to other ions. Moreover, many of these channels are gated. To simply explain the issue, consider that the pathways are closed and unavailable for transport unless specific signals are given. One of the most vital functions of gated channels is in regulating nerve conduction in animals [2].
- Organic molecules, like sugars and amino acids, can be transferred across the membrane via uniporters which carry molecules along the concentration gradient. Almost all tissues in any living being have a variety of uniporters for transfer of glucose and amino acids into their cells.

Active Transport
Active transporters make an endergonic reaction (Keq < 1) more exergonic (Keq > 1) by coupling the first reaction to a second highly exergonic reaction (e.g., ATP-hyrolysis) through common intermediates to change the direction of transport (e.g., Na export from low to high concentration) [3]. To be more precise, when a transfer is not electrochemically favorable, another source of energy (which can come from another reaction) is required to force the transfer. These can be accomplished by a direct result of ATP hydrolysis (ATP pump) or by coupling the movement of one substance with that of another (symport or antiport) [2]. Active transport may use energy to transport solutes into or out of the cell, but always in opposite direction of the electrochemical driving force.
As mentioned before, biomembranes separate the intracellular and extracellular environments that are different in many aspects such as concentration levels of ions and chemicals. For example, in human tissues, all cells have a higher concentration level of sodium ion outside the cell than inside, while the exact opposite condition is maintained for the potassium ion (Cinside > Coutside). Regarding charged solutes and ions, besides the concentration gradient, the electrical voltage can come to play too; there is an electrical driving force for cations and anions to move along and opposite the electric field, respectively.
Like pushing an object uphill against the gravitational field, moving a molecule against its favorable electrochemical driving force requires energy. In this respect, biological cells have evolved active protein transporters that can transfer ions and charged molecules in an electrochemically unfavorable direction.
In theory, active transport can be explained by a simple fact: Standard Free Energy Changes are Additive. Consider two reactions:
This rule can show how an endergonic reaction (Keq < 1) can shift to the RHS (producing more product) by being coupled to another highly exergonic reaction (Keq >> 1) through a common intermediate [3]. To clarify the issue let us consider the active transport of the sodium ion as follows:
- Reaction 1: Ion Transport
The ion transport equation can be written as
ΔG=RTlnCoCi+zFV
which for Na+ gives the Gibbs free energy of 2.98 kcal/mol, or equivalently, an equilibrium constant of 0.0065. In this equation, R is the universal gas constant (1.987 cal/(mol.K)), T is absolute temperature (K), F is the Faraday's constant (23060 cal/(volt.mol)) and z is the the valence (charge number) of the ion. Moreover, subscripts i and o denote the inside and outside of the cell.
- Reaction 2: ATP Hydrolysis
As mentioned before, the required excess energy for active transport can come from ATP hydrolysis. Typical Gibbs free energy change for ATP hydrolysis is around -13 kcal/mol, making the total Gibbs free energy change of 2.98 - 13 = -10.02 kcal/mol. Therefore, the overall reaction is highly shifted to produce more product by being coupled with the strictly exothermic ATP hydrolysis reaction.
Osmosis: Water Permeability
Osmosis (transfer of water molecules through the bilayer) is a function of the relative concentration levels of solute molecules in intracellular and extracellular environments. Water molecules can readily pass through special protein channels. If the total concentration of all dissolved solute is unbalanced (Cinside ~= Coutside), there would be a net water flow into or out of the biological cell [5]. The direction and magnitude of the water flow is strictly dependent on whether the cell’s environment is isotonic, hypotonic, or hypertonic which are illustrative measures for the relative concentrations of solutes inside and outside the cell.
Isotonic Solutions (Cinside = Coutside)
In isotonic case, the total molar concentration of dissolved solutes is the same for the intracellular and extracellular environments. In this condition, the inward and outward flows of water molecules are exactly balanced (shown in Figure 4.1.4). As shown in Figure 4.1.4, the net flow of water is zero and total number of water molecules (or equivalently water concentration, Cw) is remained constant on each side. A 0.9% solution of sodium hydroxide is a perfect example of isotonic solution to animal cells [2]. During experiments, like exposing membranes to different solutions, it is highly recommended to use an isotonic solution to prevent osmotic effects (e.g., swelling and shrinking of the cell) which can seriously damage the biological cells.

Hypotonic Solutions (Cinside > Coutside)
In a hypotonic condition, molar concentration of the total dissolved solutes is higher inside the cell than that in the extracellular environment. Obviously, low concentration of solutes in an aqueous solution can be interpreted as high concentration of water. Therefore, it is straightforward to see if Cinside > Coutside → Cw, inside < Cw, outside, providing a driving force for a net inward water flow to the cell. Hence, when a cell is exposed to such hypotonic conditions, there is net water movement into the cell and passing time, the concentration of water molecules inside the cell would be increased. Because of this considerable accumulation of water molecules, cells will swell and may even burst if the excess accumulated water is not removed from the intracellular environment.
Hypertonic Solutions (Cinside < Coutside)
Cell behavior under hypertonic condition is exactly the opposite of what explained for the hypotonic case (Cinside < Coutside → Cw, inside > Cw, outside). In this case, the water concentration is higher in cell's interior than in its outside, so there would be a net outward water flow from the cell. Therefore, passing time, the water concentration level will decrease inside the cell and cell will shrink. As an important consequence of the low water level, the ability of cell to function or divide would be gradually lost [2]. It is interesting that hypertonic solutions like concentrated syrups have been used since ancient times for food preservation. This can be explained through the fact that microbial cells that would cause spoilage are dehydrated in these very hypertonic environments and would be unable to function [2].
Transport Disorders
Considering the remarkable specificity of the transporters, it is not surprising that sometimes there are defects in transport systems. Nowadays, several different diseases known to be due to transport defects. In many of the cell membrane diseases, proteins do not transport materials properly. Some of the membrane transport disease are hereditary. An archetypical example of such transport diseases is Cystinuria, an inherited autosomal recessive disease that is characterized by abnormally high amino acid (cystine) concentration level in the urine, that may result in the formation of cystine stones in the kidneys. Another example can be Cystic Fibrosis (CF) which is caused by a mutation in the cystic fibrosis transmembrane conductance regulator, CFTR, a protein that helps move salt and water across the membrane. It is a genetic disorder that affects mostly the lungs but also the pancreas, liver, kidneys, and intestine. Long-term issues include breathing problems and coughing up mucus as a result of frequent lung infections. In a patient with CF, the cells do not secrete enough water; when it happens in the lungs, it causes the mucus to become extremely thick.
It is also worth mentioning that most fatal toxins like Dendrotoxin (black mamba snake of Africa) and Batrachotoxin (Colombian frog Phyllobates aurotaenia) act directly on specific ion channels of the plasma membrane to disrupt the action potentials. Dendrotoxin, as a presynaptic neurotoxin, blocks specific subtypes of voltage-gated K+ channels in neurons, so increasing the release of acetylcholine at neuromuscular junctions. In this regard, a single dendrotoxin molecule reversibly associates with a K+ channel to apply its suppressive effect. To put it simply, this fatal toxin binds to anionic sites near the extracellular surface of the channel and physically blocks the path and ion conductance. Batrachotoxin on the other hand, as an extremely cardiotoxic and neurotoxic steroidal alkaloid, works by binding to the Na+ channel and causing a conformational change (modifying both their ion selectivity and voltage sensitivity). In a nutshell, batrachotoxin irreversibly binds to the sodium channels, enforcing them to remain open.
Driving Forces
The permeability of a membrane can be defined as the passive diffusion rate of permeated molecules across the biomembrane. It is unanimously accepted that permeability of any specific molecule depends mainly on charge number, polarity, size, and to some extent, to the molar mass of the molecule. It should be noted though that both the nature of the bilayer and the prevalent environments can play a significant role too. As mentioned before, because of the inevitable hydrophobic nature of the biomembranes, small uncharged molecules pass across the membrane more easily than charged, large ones [6].
With charged species (e.g., Na+), the effect of the membrane potential (V) should be taken into account. Most cells are characterized by a membrane potential difference of -70 mV (Vinside - Voutside). Let us first consider an example of Cl- ion to clarify the issue. For Cl-, the concentration gradient is toward inside the cell (CExtracellular = 125 mM & CIntracellular = 9 mM). So, there is a driving force of diffusion for Cl- to diffuse along the concentration gradient into the cell. However, the electric field is directed into the cell (Vinside < Voutside), pushing out negatively charged ions. Therefore, an equilibrium is achieved when influx and efflux of Cl- level each other. The membrane potential at which this equilibrium occurs is called equilibrium potential that can be calculated by Nernst equation [7]:
\[V_{\text {equilibrium}}=\frac{R T}{F_{Z}} \ln \left(\frac{C_{o}}{C_{i}}\right)]
Note that this relation was obtained from ion transport equation for zero Gibbs free energy change (i.e., thermodynamic equilibrium).
Then, it would be useful to define a driving force potential difference as VDF = Vcell - Vequilibrium. By this definition, negative VDF means passive uptake and exit of cations and anions, respectively. For example, for the case of Cl-, VDF = 0.3 mV indicating diffusion of Cl- into the cell. The same is true for Na+ where VDF = -127.3 mV. However, this is not the case for other ions like K+ which will be pushed out by the net electrical potential VDF of 11.2 mV.
Moreover, huge VDF values (big difference between Vcell and Vequilibrium) of some ions such as Na+, K+, and Ca+ suggest that there are other forces besides the chemical and electrical gradients needed for the transport. In such conditions, passive (protein channels) or active transporters are required for the ion transfer.
Permeability Model
Schematic diagram of diffusion through a bilayer is sketched in Figure 4.1.5 in which two aqueous solutions S1 and S2 are separated by the biomembrane. Superscripts "aq" and "m" denote solute concentrations at bulk aqueous solutions and surfaces of the membrane, respectively. As it can be seen, the concentration gradient is considered to be from S1 to S2, providing the chemical driving force of the transport. To mathematically describe the permeability, let us first introduce the useful concept of partition coefficient. At thermodynamic equilibrium, the equality of the chemical potentials of solute j in two different intracellular and extracellular phases can be expressed as
μji+RTlnCji=μjo+RTlnCjo
Then, the partition coefficient can be defined as
Ki/o=CjiCjo=exp(−(μji−μjo)RT)
Having the partition coefficient, the mass flux (mol/(m2.s)) across the membrane (Figure 4.1.5) is given by
J=K1/2Dλ(C1−C2)
where D denotes the ion diffusivity through the membrane and K1/2 is the partition coefficient of the two phases (the ratio of solubilities in lipid and water). Finally, the mass transfer coefficient in above equation is simply called permeability (in units m/s) of the solute diffusion through the membrane:
P=K1/2Dλ
References
- Biological Membranes. Wikipedia: https://en.Wikipedia.org/wiki/Biological_membrane
- Pearson Practice Hall - Lab Simulations. www.schenectady.k12.ny.us/putman/biology/data/biomembrane1/intro.html
- W. D. Stein. Transport and Diffusion across Cell Membranes. Academic Press, 1986.
- Selectively Permeable Membranes. Study.com: http://study.com/academy/lesson/selectively-permeable-membranes-definition-examples-quiz.html
- R. Fettiplace & D. A. Haydon. Water Permeability of Lipid Membranes. Physiological Reviews 1980 (60) 510 - 550.
- Cell Membrane. Wikipedia: https://en.Wikipedia.org/wiki/Cell_membrane#Permeability
- Nernst Equation. Wikipedia: https://en.Wikipedia.org/wiki/Nernst_equation

