1.7: Examples of 2-Dimensional Motion

Circular Motion

Using what we just derived regarding the parallel and perpendicular components of acceleration, we turn now to the special case of an object traveling in a circle. The parallel part of the acceleration obviously always points tangent to the circle, which narrows it down to two directions at any given point on the circle. If the object is speeding up, then of course the tangent points in the direction of motion, and if it is slowing down, the tangent vector points in the direction opposite to the motion. The perpendicular part must be at a right angle to this tangent, which means it must be toward or away from the center of the circle. Unlike the tangent case, however, both directions are not possible. We can see this by considering the average perpendicular acceleration vector over two nearby moments in time:

Figure 1.7.1 – Direction of Centripetal Acceleration

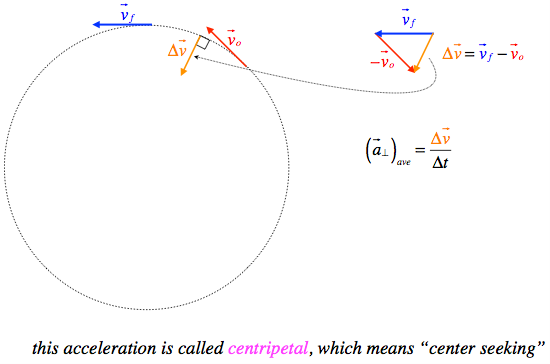
What is the magnitude of this centripetal acceleration? Well, it depends upon how fast the object is going (the faster it is moving, the more acceleration is required to turn in the same circle), and the radius of the circle (the acceleration is greater when the radius is smaller). Deriving the magnitude is left as an exercise, but the answer comes out to be:

\[ |\overrightarrow a_c | = \dfrac{v^2}{r} \]

Sometimes circular motion is the result of something rotating. For example, a bug on the outer rim of a rotating turntable travels in a circle, and therefore experiences centripetal acceleration. Well, when we deal with rotating objects we often know only the rate of its rotation (say in units of revolutions per minute), and we have to translate into linear motion to know the speed. There is a simple and standard way to do this.

Digression: Radians

If we are talking about rotational motion, we need to discuss how we measure such motion. We clearly don’t measure the speed of a spinning top or turntable in terms of meters per second, but rather how much it turns in a period of time. How does one measure the angle through which something turns? One way is to divide the full circle up into 360 equally-sized pie slices. The magnitude of one of these angles we call a 'degree.' But really this division is arbitrary. So why was 360º selected? Well, given that we often have to deal with slices of pie, we can avoid having to use fractional degrees if we select a number with lots of factors, and 360 certainly fits the bill – it is divisible by 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 120, and 180.

But there is no reason at all that divisibility needs to be our only criterion. In fact, we don’t even need to divide the circle into an integral number of pieces. For example, we could divide it into 7.5 pieces and call the size of each piece “1 flibber.” We can even translate between different systems of units: \(1^f\) = 48º.

But there is another criterion that leads to a definition of a measurement of angles that is different from degrees. Suppose we want a simple translation from angle to arclength (the distance traveled along the circular curve subtended by that angle). We know that traveling around an entire circle requires a journey of a distance equal to \(2 \pi\) times the radius of the circle. So going around some fraction of a circle requires a journey equal to that fraction times \(2 \pi r\). So if we divide the circle into an uneven number of pieces such that \(2 \pi\) of these pieces fit into the circle, then in these units you can calculate the arclength by just multiplying the angle measured in those units (called radians) by the radius of the circle:

\[ s = r \theta, \ \theta \ \text{measured in radians} \]

If we want to translate between the speed that something is going around the circle to the angular speed at which the slice of the pie is being swept-out by this motion, we need only take a derivative:

\[v = \dfrac{ds}{dt} = \dfrac{d}{dt} \left( r \theta \right) = \cancelto{0}{\dfrac{dr}{dt}}\theta + r \dfrac{d\theta}{dt}\; = r \omega, \;\;\;\;\;\;\;\; \omega \equiv \dfrac{d\theta }{dt} = rate\;of\;rotation\;in\; \dfrac{rad}{s}\]

This gives us an alternative way of expressing the centripetal acceleration:

\[ | \vec a _ c | = \frac{v^2}{r} = \frac{\left( r \omega \right) ^2}{r} = r \omega^2 \]

Analyze This

A bead is threaded onto a circular hoop of wire which lies in a vertical plane. The bead starts at the bottom of the hoop from rest, and is pushed around the hoop such that it speeds up at a steady rate.

Analysis

The tangential motion of the bead is in one dimension, so we can use the usual kinematics equations to describe its motion along the circle. That is, equations like:

\[x\left(t\right)=x_o+v_o t +\frac{1}{2}at^2\nonumber\]

can be used here, where the displacement \(\Delta x=x-x_o\) is the distance measured around the arc of the circle. So if the bead goes all the way around, then \(\Delta x\) is just the circumference of the circle.

The fact that the bead "speeds up at a steady rate" means that the part of the bead's acceleration in its direction of motion (i.e. tangent to the circle) is a constant.  This is not to say that the acceleration of the bead is constant, however.  Its motion is changing direction, which means that there is a component of acceleration perpendicular to its velocity (in this case, centripetal).  Given that the magnitude of centripetal acceleration depends upon the radius of the circle (which in this case doesn't change) and the speed of the object (which in this case does change), then this component of acceleration is changing in magnitude over time.

We can apply some general mathematics to this case.  If we call the constant acceleration tangent to the circle \(a\), then since it starts from rest, the speed of the bead tangent to the circle at any given time is just \(v(t)=at\). If we call the radius of the circle \(R\), then we can write down the centripetal acceleration as a function of time as:

\[a_c=\dfrac{v^2}{R}=\dfrac{a^2}{R}t^2\nonumber\]

Projectile Motion

For circular motion, we have the components of velocity changing in tandem in a specific manner to keep the path circular. Another – actually simpler – form of motion involves only a single fixed coordinate component of velocity changing, while the other components involve no change in velocity. What I am alluding to here is projectile motion, which comes about because the vertical component of motion is subject to constant acceleration (as we discussed when we talked about free-fall), while the horizontal component is unaffected by gravity’s influence. This kind of motion is only one small step from the free-fall we are already familiar with, in that it includes a totally independent horizontal component of motion that incorporates (to the extent that air resistance can be ignored) no acceleration. As simple as this sounds, a couple of examples muddy the waters a bit, and sorting them out is very instructive:

Conceptual Question

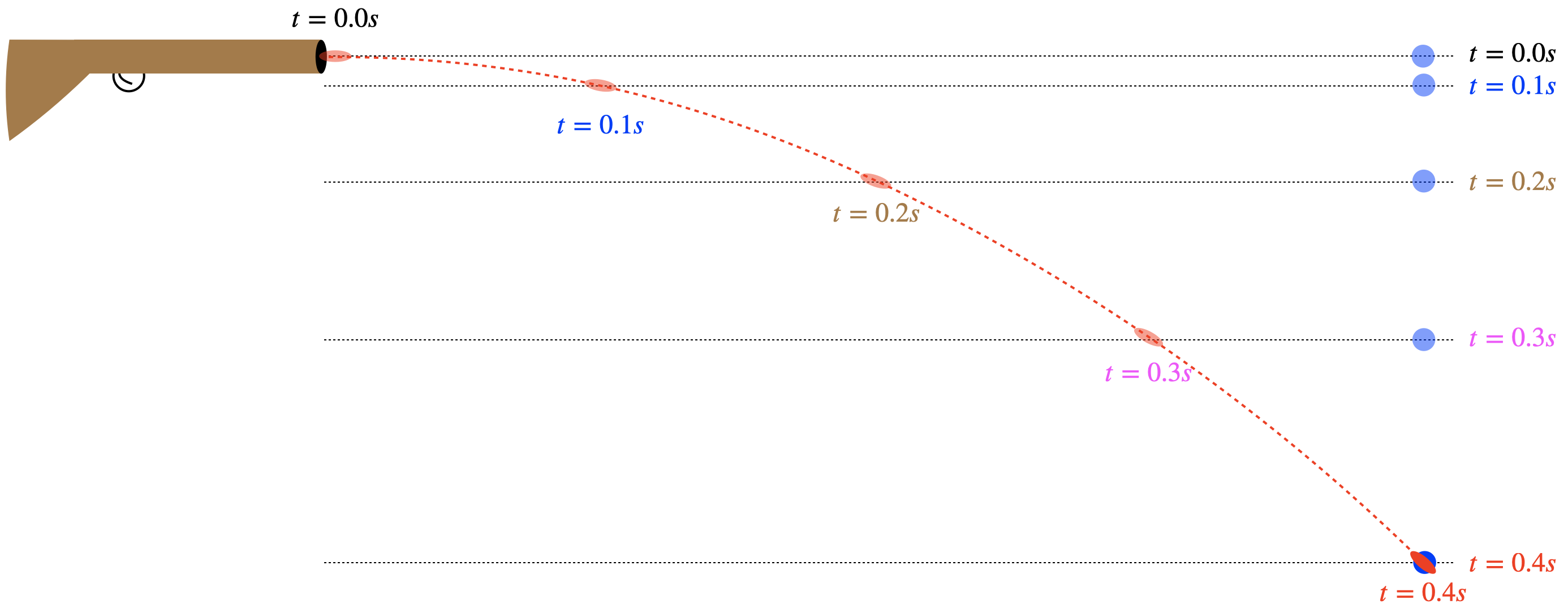
A hunter climbs a tree and fires a bullet directly at a monkey that is hanging from a branch of another tree at precisely the same height as the barrel of the hunter’s gun. The instant the bullet leaves the gun, the monkey lets go of the branch. Ignoring air resistance (and the size of the monkey - assume it is very small), what is the fate of the monkey?

1. The monkey will be hit by the bullet.
2. The bullet will pass beneath the monkey.
3. The bullet will fly over the monkey’s head.
4. Whether the bullet flies over the monkey’s head or passes beneath it depends upon how fast the bullet is moving when it leaves the barrel of the gun.
5. What kind of jerk shoots a monkey?

Solution

A (and E). The vertical motion of the monkey is independent of the horizontal motion, so in equal time spans, the bullet falls the same distance as the monkey. Since they started at the same level, they remain at the same level at all times, including when the horizontal position of the bullet equals the horizontal position of the monkey.

Conceptual Question

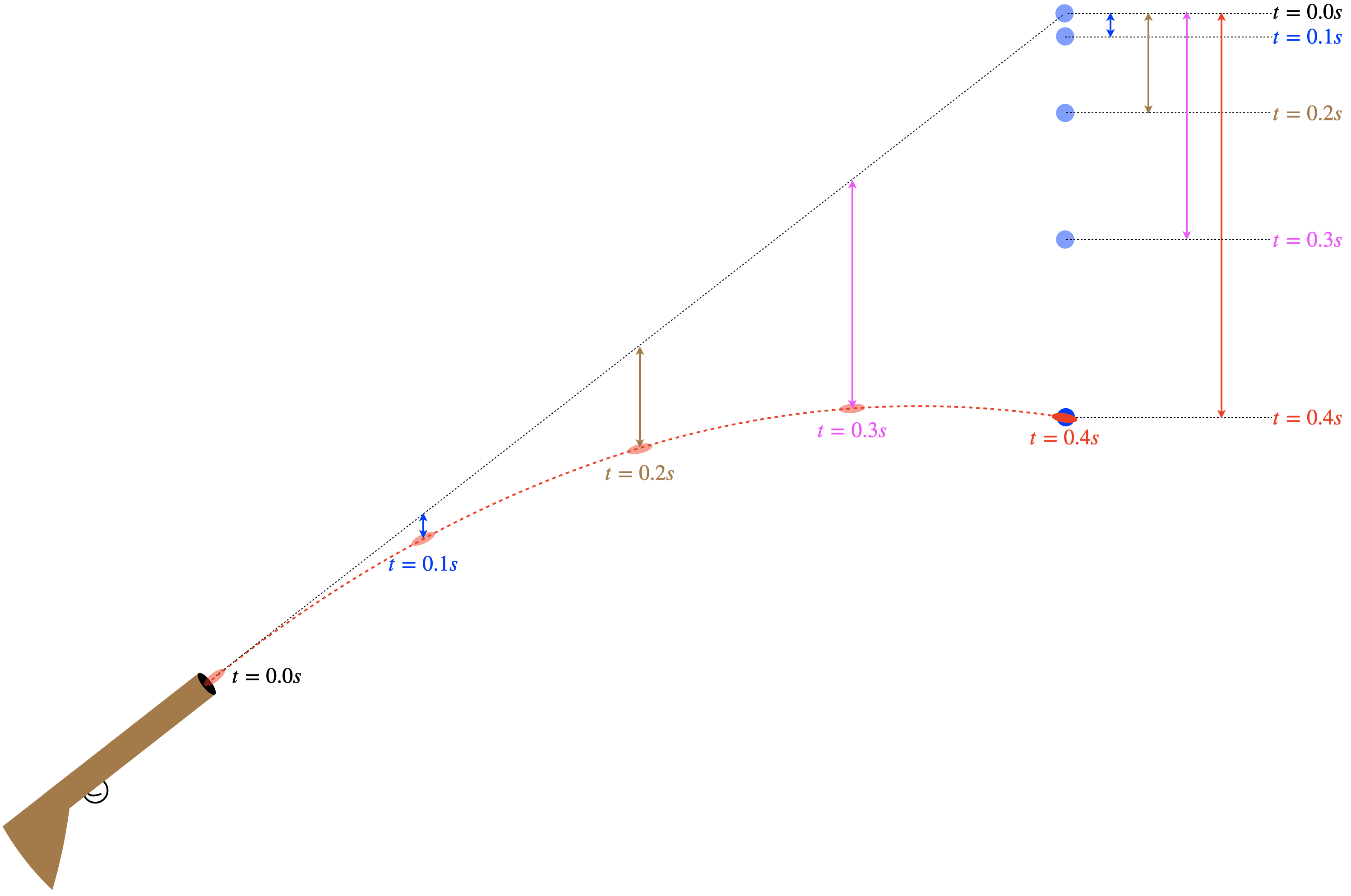
After falling out of the tree the last time he tried to shoot a monkey (his gun misfired), the hunter now decides to shoot a monkey from the ground. He is aiming upward at an angle, and is assuming the monkey will again let go of the branch just as the bullet is on its way. How should the hunter aim this time, if he is to bag his simian prize?

1. He should aim right at the monkey.
2. He should aim above the monkey.
3. He should aim below the monkey.
4. Unlike the level-shot case, where he should aim this time does depend upon how fast the bullet is coming out of the gun.
5. The jerk should just aim at himself.

Solution

A (and E). If there was no gravity, the bullet would follow a straight line to the monkey. With gravity acting straight down, the amount that the bullet drops below that straight line is the same that an object starting from rest on that straight line falls in an equal time. So the bullet and the monkey remain the same distance from the straight line at all times. When the bullet’s horizontal position equals the monkey’s horizontal position, they will coincide.

The only difference between this example and the previous one is that in the previous case, the line joining the barrel of the gun and the target was horizontal. Still, not everyone may be as convinced in this case as in the previous one, so let's do the math...

Suppose there is no gravity. The path that the bullet takes (\(y\) as a function of \(x\)) can be written down pretty easily. If the point where the bullet exits the barrel is chosen to be the origin, then the straight line to the monkey has a slope equal to the ratio of the vertical and horizontal components of velocity:

\[y=mx+b=\left(\dfrac{v_{oy}}{v_{ox}} \right)x \nonumber \]

Now suppose there is gravity. We have separate horizontal and vertical equations of motion. Again, with the bullet starting at the origin, we have:

\[x=v_{ox}t \\ y=v_{oy}t-\frac{1}{2}gt^2 \nonumber \]

Now solve for \(t\) in the first equation and plug it into the first term of the second equation to get:

\[y=\dfrac{v_{oy}}{v_{ox}}x-\frac{1}{2}gt^2 \nonumber \]

Comparing this with the first equation above, we see that the \(y\) value would follow the same straight line if not for the second term, and the amount that the height of the bullet \(y\) is decreased from that line after a time \(t\) is exactly the same distance that the monkey falls from that line in the same time.

With the number of variables and constants involved in projectile motion problems, there are countless ways to construct problems. There is no substitute for independent thinking and creativity, but the steps given below provide a good starting point for solving these kinds of problems.

• Draw a picture, labeling it as completely as you can, using information you have been given. Then spend some time thinking about what is happening – put yourself into the situation.

Alert

While this is given as a step for projectile problems, this is actually how you should start every physics problem!

• Pick an \(x\), \(y\) origin as well as \(+x\) and \(+y\) directions. Often for projectile problems up is chosen as the positive direction (making the acceleration due to gravity a negative value), but this is by no means required. What is important is that you use the positive direction consistently throughout the constants and variables in the equations.
• Break any initial velocities into components along the \(x\) and \(y\) directions.
• Write down the equations of motion, circling quantities that you know, and underlining the number you are looking for. If you have too many un-circled quantities for the number of equations available, you cannot yet do the algebra, so you’ll need to review the statement of the problem for any values concealed in the language of the problem (if you just scan a problem for numbers without carefully reading it, you will miss these).
• Solve the algebra and reconstitute components back into vectors, if necessary.
• Briefly check to see if the answer makes sense.

Alert

This is actually how you should end every physics problem!

One thing in projectile motion that is a useful tool is known as the range equation. This was of particular use to military firing cannonballs or (farther back in history than that), catapults. This equation relates the distance that a projectile will fly assuming it lands at the same vertical position that it started, given the starting speed of the projectile and the starting angle. Let’s treat finding this equation as if it was a projectile motion problem given to us, and follow the procedure outlined above

Analyze This

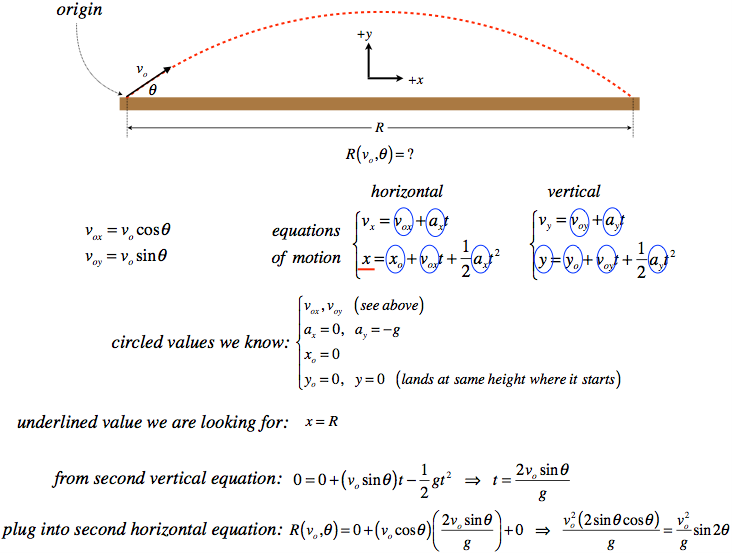
A cannonball is fired at an angle \(\theta\) up from the horizontal at a speed of \(v_o\), along level ground. Ignore air resistance in your analysis.

Analysis

The diagram below labels the origin and the + directions. It sure seems like knowing the initial angle and speed (as well as the fact that the ground is level) should be sufficient to determine how far the cannonball travels. We will therefore look for \(R\) (referred to as the "range") in terms of the initial speed \(v_o\) of the projectile and the launch angle \(\theta\), which we treat as known values. The rest of the procedure and algebra is given below.

It is interesting to note that for any given launch speed, there are in general two (complementary) angles that correspond to the same range (except for \(45^o\)).  For example, a cannonball fired at \(\theta=50^o\) will land at the same place as a cannonball fired at the same speed at an angle of \(\theta=40^o\).

It is also possible to determine the angle at which the range is maximized for a given velocity. Treating \(v_o\) as a constant and maximizing the function \(R\left(\theta\right)\) gives:

\[0=\dfrac{dR}{d\theta}=2\dfrac{v_o^2}{g}\cos 2\theta\;\;\;\Rightarrow\;\;\;\theta=45^o\nonumber\]

Analyze This

Two warlords aim identical catapults (i.e. they both release rocks at the same speed) at each other, with both of them being at the same altitude. The warlords have made the necessary computations to crush the other, and fire their catapults simultaneously. Amazingly, the two stones do not collide with each other in mid-air, but instead the stone Alexander fired passes well below the stone that Genghis shot.

Analysis

These are two projectiles fired with equal speeds to equal ranges, but using the result from the previous analysis box, we know they must have been fired at complimentary angles.  While the ranges are the same, the times are not, since the time for the full flight is twice the time from the apex to the ground, which means that the projectile fired at the lower angle (which will reach a lower peak height) will reach its target first.  Because Alexander's stone passes below Genghis's stone, it must have a greater \(x\) component of velocity, which means that when the stones pass by each other, the crossing point must be closer to Genghis than Alexander, and Alexander's stine is on the way down, while Genghi's is still on the way up.  It looks something like this:

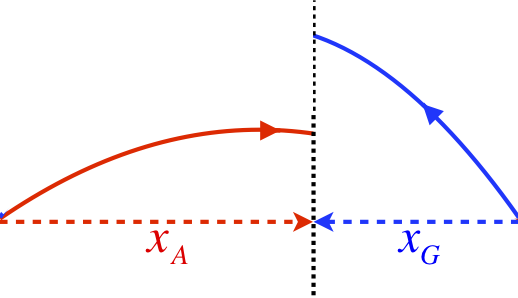
If we knew something about the times these projectiles take to hit their targets, we could relate the (constant) \(x\)-components of their velocities. Combining this with the knowledge that they have equal total speeds and are fired at complementary angles gives us a lot to work with.