8.1: Simple Harmonic Motion
- Page ID
- 63018
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Equation of Motion for an Elastic Force
We have discussed the idea of a restoring force a few times already. If such a force counteracts displacements in both directions of one-dimensional motion, then it can cause the object to move back-and forth across the equilibrium point: An object subject to a restoring force is displaced from its equilibrium point and released. It accelerates toward the equilibrium point thanks to the restoring force. Upon arrival at the equilibrium point, it doesn't stop, because the restoring force is zero there. As it continues past, the restoring force acts to slow down and eventually stop the object, whereupon the object accelerates back toward the equilibrium point and the motion repeats in the opposite direction. This is called oscillatory motion, and it results from all two-way one-dimensional restoring forces.
The most common sort of restoring force we study is the elastic force. Indeed, other restoring forces occurring in nature (such as those between particles exhibiting a Lennard-Jones potential energy, as discussed at the end of Section 3.7) are often modeled as masses on springs. The oscillatory motion induced by the elastic restoring force is quite special, as we will see, and is called simple harmonic motion. We seek here the equation that relates the position of the mass as a function of time (with the equilibrium point being the origin), usually referred to as the equation of motion for this force.
Start (naturally) with Newton's second law, where the net force is simply that of a spring (Hooke's law). As we are working in one dimension, we once again have the luxury of treating our vector directions as simply (+) or (–):
\[ F_{net} = -kx = ma \;\;\; \Rightarrow \;\;\; \dfrac{d^2x}{dt^2}+\dfrac{k}{m}x = 0 \]
We seek to determine the function \(x\left(t\right)\) that satisfies this differential equation. This is actually simpler than it might at first appear, if thought about in the following way: First, let's imagine that the ratio \(\frac{k}{m}\) is just the number 1. Can we think of a function that after two derivatives becomes the negative of itself? We don't know a whole lot of special functions, but amazingly, there are actually a couple that do satisfy this: sine and cosine. The derivative of sine is cosine, and then a second derivative brings it back to negative sine.
There are lots of different features we can include with a sine (or cosine) function, so let's write one out in all its glory:
\[ x\left(t\right) = A \sin\left(\omega t + \phi\right) \]
Two derivatives of this function gives:
\[ \dfrac{d^2}{dt^2}\left[A \sin\left(\omega t + \phi\right)\right] = \dfrac{d}{dt}\left[\omega A \cos\left(\omega t + \phi\right)\right] = -\omega^2 A \sin\left(\omega t + \phi\right) \]
Plugging this into the differential equation gives a solution if we have:
\[ \omega = \sqrt{\dfrac{k}{m}} \]
Total Phase
It may seem crazy at this point to introduce the greek letter \(\omega\) as a constant here when we so recently used it as a measure of angular velocity, and there is no rotational motion going on here. But there is a good reason to do this. Consider a bead moving at a constant speed on a circular loop of wire of radius \(A\).
Figure 8.1.1 – Bead Moving on a Circular Loop of Wire
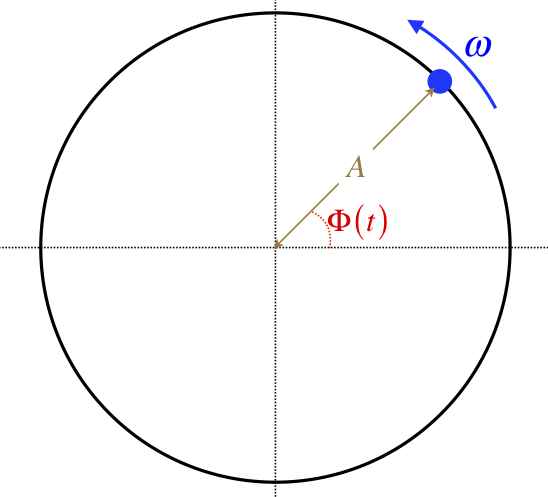
The equation describing its motion is something we are quite familiar with:
\[ \Phi\left(t\right) = \omega t + \phi \]
We have changed notation a bit here from what we used previously for circular or rotational motion: \(\Phi\left(t\right)\) represents the total angle traversed, in place of our previous \(\theta\left(t\right)\), and \(\phi\) represents the starting angle at \(t=0\), in place of our previous \(\theta_o\).
Next let's imagine placing a light source to the left of this loop, and a screen (the plane of which is perpendicular to the plane of the loop) to the right of the loop. The light would project a shadow of the bead onto the screen, and the motion of this shadow can be described mathematically:
Figure 8.1.2 – Motion of a Projection of a Bead moving on a Circular Loop
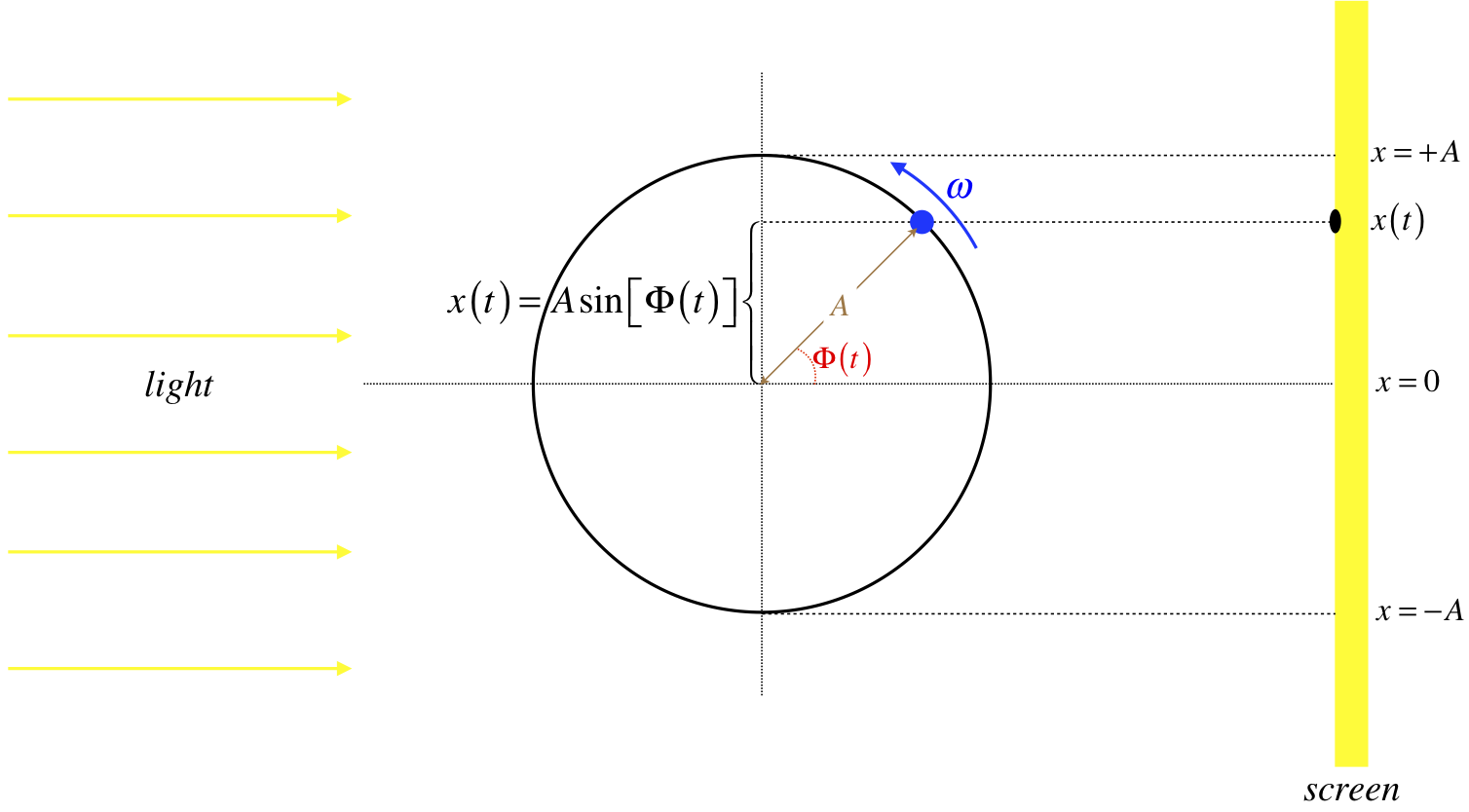
The motion of the shadow is simply a component of the motion of the bead – if we know the angle the bead makes on the circule, we know the height of the shadow on the screen. In terms of the starting angle and angular velocity of the bead, the motion of the shadow can be written explicitly as:
\[x\left(t\right) = A\sin\left(\omega t+\phi\right) \]
This is precisely the same as the equation of motion of a mass on a spring, Equation 8.1.2. That is, if we placed a mass on a spring at the screen with the equilibrium position at \(x=0\), pulled the spring to a maximum stretch (or pushed it to a maximum compression) of \(x=A\), and then waited for the shadow to land on the mass before releasing it, the shadow would remain on the mass as it moves, if the angular velocity of the bead happens to equal \(\sqrt{k/m}\).
We can now discard our bead-on-circular-loop model, but we keep the mathematical structure it leaves behind. The argument of the sine function \(\Phi\left(t\right)\) is called the total phase of the harmonic motion of the mass-on-spring. The maximum expansion/compression of the spring \(A\) is called the amplitude of the harmonic motion. The constant \(\omega\) is referred to as the angular frequency (not angular velocity – we've left the bead model behind), and still is expressed in units of radians per second. This constant sometimes gives way to a frequency \(f\) that is measured in cycles per second (or hertz), with the translation between the two being:
\[\omega = 2\pi f \]
The period of oscillation is the time it takes the system to come all the way back to where it started, and as the time per cycle, it is the inverse of the frequency:
\[T = \dfrac{1}{f} = \dfrac{2 \pi}{\omega} = 2\pi \sqrt{\dfrac{m}{k}} \]
Alert
The period is the time required for the system to complete a full cycle, which is not the same as the time required for the mass to return to a previous position. The mass must return to the same position and it must be moving in the same direction. In other words, the total phase \(\Phi\) must change by \(2\pi\).
And finally, the constant \(\phi\) is called the phase constant, and it carries the information of where the mass is at time \(t=0\).
Kinematics of Harmonic Motion
Once we have a formula for the position of an object following simple harmonic motion, we can use the usual calculus tools to determine the velocity and acceleration at various times as well. The velocity as a function of time is:
We note a couple of features of this result. First, since the cosine function never exceeds 1, we have the maximum speed of the object:
\[v_{max} = A\omega =A\sqrt{\dfrac{k}{m}} \]
And second, this maximum speed is achieved at \(x=0\) (the equilibrium point), which makes sense, since the spring was accelerating it toward that point, and immediately after passing it, the spring starts slowing it down.
The acceleration of the mass as a function of time we get from another derivative:
\[a\left(t\right) = \dfrac{d}{dt} v\left(t\right) = \dfrac{d}{dt} \left[A\omega\cos\left(\omega t+\phi\right)\right] = -A\omega^2\sin\left(\omega t+\phi\right)\]
The fact that this result is only different from the position function by a factor of \(\left(-\dfrac{k}{m}\right)\) brings us back to what started all of this, Equation 8.1.1.
Mechanical Energy
We already know that the elastic force is conservative, so mechanical energy is conserved during simple harmonic motion. At any given time during the motion, the mass will have kinetic and potential energy, with its total energy remaining constant. It's easy to write an expression for the total energy in this system by choosing a convenient point in the motion – when the mass is stationary. This occurs when it reaches its maximum separation from the equilibrium point, i.e. when the displacement equals the amplitude:
\[E_{tot} = \frac{1}{2}kx_{max}^2 = \frac{1}{2}kA^2 \]
We can double-check this result by looking at the moment in time when there is zero potential energy and all of the mechanical energy is kinetic – at the equilibrium point. Using Equation 8.1.9, we get:
\[E_{tot} = \frac{1}{2}mv_{max}^2 = \frac{1}{2}m\left(A\sqrt{\dfrac{k}{m}}\right)^2 = \frac{1}{2}kA^2 \]


