1.17: Cosmological Data Analysis
( \newcommand{\kernel}{\mathrm{null}\,}\)
We focus in this chapter on the analysis of cosmological data. Most of what I present in this chapter applies much more broadly; in fact, nothing in this text book is of broader utility. However, the presentation here is entirely focused on application to cosmology. We wish to learn from measurements of the cosmos. These measurements are never 100% precise, and thus we need a means of dealing with uncertainty. We necessarily deal in probabilities.
This is especially true for the practitioner interested in discovering something new. Almost always, the data are not overwhelmingly and obviously convincing of the new truth that they potentially reveal. Data analysis in cosmology is an exciting process of sorting out whether one is on the cusp of an exciting discovery, or on the cusp of embarrassing oneself by claiming something that turns out not to be true. It calls for rigor of process and high integrity. Engaging in it, in the right way, will raise one's standards of what it means to know something. One needs to search not only for the evidence that supports one's hunch of what's going on, but also, very importantly, one needs to search for evidence that supports alternative explanations. We are after the truth.
There are two distinct aspects of data analysis: model comparison and parameter estimation. In model comparison we try to determine which model is better than another. In parameter estimation, we have one assumed model and we are estimating the parameters of that model. We focus here on parameter estimation.
Modeling data: a simple example
Let's start by considering a simple measurement of length, to have a specific example in mind. The signal would be the true length, ℓ, and our model of the data might be
d=ℓ+n
where d is the measurement (our data) and n is the error in the measurement, the difference between the data and the true length, ℓ. We are fundamentally interested in the probability distribution of the length, given this data. The length is the one parameter of our model. (More generally, we are interested in the joint probability distribution, given the data, of all the parameters of our model.)
A measurement, if it is to mean anything at all, has to come along with an estimate of the uncertainty in the measurement. How to estimate the uncertainty is a subject we won't explore here. We are going to assume the measurement has been done and the uncertainty in it has been accurately determined. We will further assume here for simplicity that the uncertainty can be described with a normal distribution. In our one-dimensional example this means that
P(n)=1√2πσexp(−n22σ2)
is the probability density for the error, n. What is a probability density you ask? This one tells us the amount of probability that there is between n and n+dn: it's equal to P(n)dn. The pre-factor out in front of the exponential is there to keep P(n) properly normalized so that
∫∞−∞dnP(n)=1.
It should integrate to 1 because n takes on one and only one value (even if we don't know what that value is).
A fundamentally important quantity is the probability of some data, d, given the signal s (or, in our example, ℓ ). Since n=d−ℓ we can write
P(d|ℓ)=P(n)=1√2πσexp(−(d−ℓ)22σ2)
as the probability density of d given that the length is ℓ. That is, if we knew the true length was ℓ then how probable is it to have d in the range [d,d+dd]? Answer: P(d|ℓ)dd. (What we mean here by dd is an infinitesimal increment to d).
Bayes' Theorem
Although we have an expression that tells us the probability of the data given the true value of the underlying parameter, we are actually in a position of wanting the exact opposite! We know what the data is and we desire to know what the true length is -- or, more preciesly, since we can't have perfect knowledge of the length, our goal is to know the probability that the length takes on any particular value: we want P(ℓ|d). Bayes' theorem helps us get from one to the other. It follows from fundamental axioms of probability theory. For simplicity, for the purposes of deriving Bayes' theorem, we are going to start considering discrete outcomes, like we get with the flip of a coin, or the roll of dice. Let's introduce the joint probability P(A,B where A might be a particular outcome for a six-sided die and B might be the sum of that outcome with that of another die. I've purposely constructed this example so that A and B are not independent. By the joint distribution, we mean that P(A,B) tells us the probability that the first quantity is A and the second quantity is B.
I'll give you the calculation of P(A=3,B=8). There's only one way for this to happen. The first die turns up 3 and the second one turns up 5. With a roll of two die this is one of 36 possible and equivalent outcomes, so the probability is 1/36. Of course, the probability that B<A is zero.
Exercise: Calculate these probabilities given the above definition of A and B: P(A=5,B=6), P(A=5,B=3),P(A=3,B=7).
It is a fundamental rule of probability that P(A,B)=P(A|B)P(B). The joint distribution is symmetric so it is also true that P(A,B)=P(B|A)P(A).
Exercise: From the preceding two equations derive P(A|B)=P(B|A)P(A)/P(B).
In our special case of interest, if we call our model parameters θ this becomes Bayes' theorem:
P(θ|d)=P(d|θ)P(θ)P(d).
Bayes' theorem describes learning from data. When we learn something, we're usually not starting from complete ignorance. The factor P(θ) is called the prior probability distribution, or simply, 'the prior.' It represents what we know about the model parameters prior to examining the data. The probability density P(d|θ) (at least when thought of as a function of \theta) is called the likelhood. The denominator, P(d), I find difficult to understand conceptually. It's the probability of the data, but we know the data. That's confusing. But there is an easier way to think about it for purposes of parameter estimation: it is just a normalizing constant. The reason we can do this is that, by assumption, the model is correct and so θ must take on one value; i.e., if we integrate the posterior over all possible values of θ then it must be equal to 1. Forcing this to be true will determine the value of P(d) if one knows the likelihood and the prior. One can do the integral without knowing P(d) because P(d) does not depend on θ.
The term on the left-hand side of the above equation is called the 'posterior probability distribution', or sometimes simply 'the posterior.' Getting back to thinking of Bayes' theorem as a description of learning from data, we can now see that the likelihood serves to update our prior beliefs, incorporating what we've learned from data, and what we know already, into the posterior probability distribution for θ; i.e., what we know about θ after we have studied the data. Usually we don't care about the normalization -- we just want to know how probable one value of θ is compared to another.
Modeling measurements of supernova apparent magnitude
Let's now turn to the case of modeling our supernova data. Let's take the model parameters to be θ={M,ΩΛ,Ωm,H0}. The data we take to be the supernova apparent magnitudes. The likelihood we take to be normally distributed (as we are assuming the errors in the magnitudes are normally distributed). Therefore we have
L(θ)=P(d|θ)∝exp(−χ2/2) ; χ2=Σi(mdi−mmi)2/σ2i
where
mmi=M+5log10(DL(H0,ΩΛ,Ωm;zi)Mpc)+25.
We take a prior that is uniform in ΩΛ,Ωm and H0 and normally distributed in M so that
P(θ)∝exp(−χ2M/2) ; χ2M=(M−(−19.26))2/σ2M
with σM=0.05. This mean and σ for M is consistent with the Riess et al. (2018) determination of the Hubble constant with a standard error of 2.2%, assuming that uncertainty is entirely due to uncertainty in supernova absolute magnitude calibration. We can now take the above prior and the above likelihood and multiply them together to form the posterior (up to an unknown normalization constant that we don't care about).
Marginalization
It is often the case that we do not care about all the parameters of our model. Maybe we only care about Ωm and ΩΛ. In that case we might want to calculate P(Ωm,ΩΛ|d). This probability density should include the probability associated with all values of the other parameters. It is related to the full joint distribution by integration over the other parameters via:
P(Ωm,ΩΛ|d)=∫dH0dMP(H0,ΩΛ,ΩΛ,M|d).
This process of integrating over parameters is called marginalization.
Contour plots
A common way of presenting a two-dimensional probability distribution is a contour plot. The axes of the contour plot are the two parameters, and the contours indicate curves of constant probability density. Often there will be two different curves plotted: one that encloses 68% of the probability and another that encloses 95% of the probability. The enclosed regions are the 68\% confidence region and the 95% confidence region, respectively.
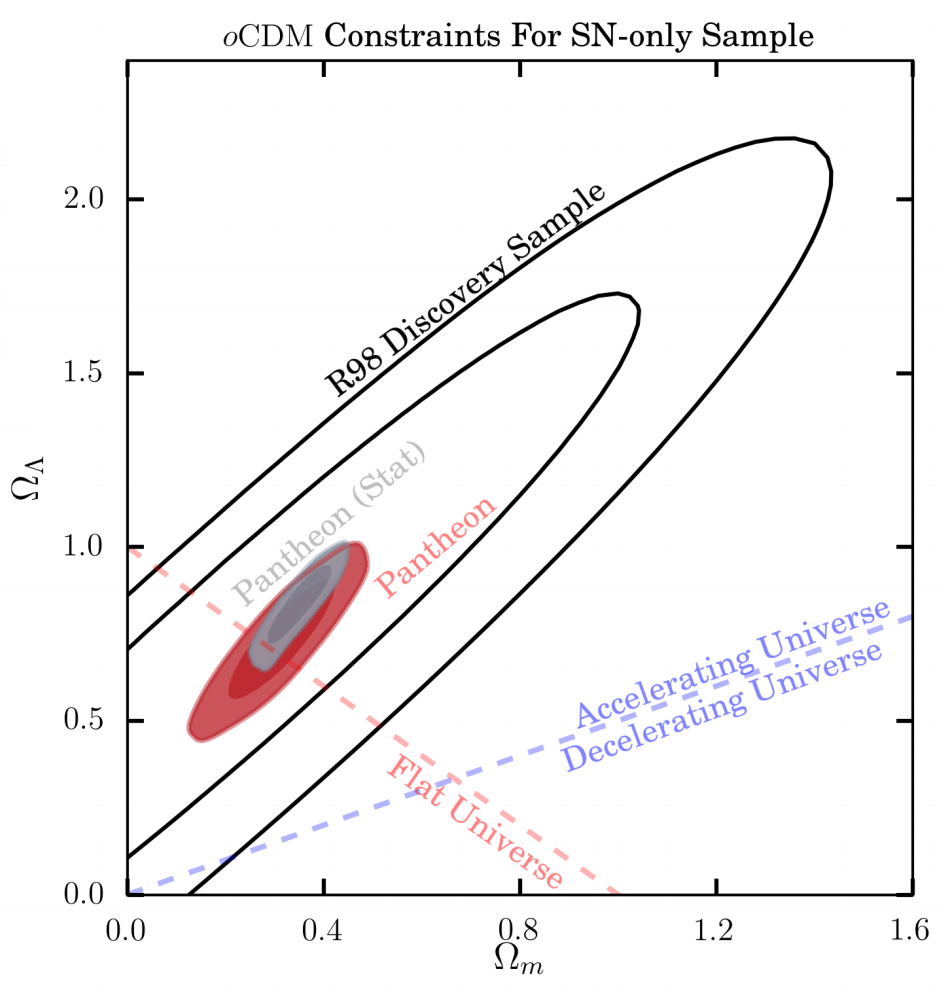
An example contour plot is shown in the figure at the beginning of this chapter. The contours labeled "R98" discovery sample give the 68% and 95% confidence regions given the Riess et al. (1998) data that were used for the discovery of cosmic acceleration. The red and dark red shaded regions are the 68% and 95% confidence regions, respectively, given the Scolnic et al. (2018) supernova data, but only taking into account some of the sources of error. The authors distinguish some of their errors as systematic, as opposed to statistical. Including the systematic errors as well leads to the grey contours. The shrinkage from the R98 contours to the gray contours indicates the progress that has occurred in supernova cosmology over the 20 years from 1998 to 2018.
If the probability density is Gaussian then the contours are such that 2ln(Ppeak/P68)=2.3 and 2ln(Ppeak/P95)=6.17, where Ppeak is the probability density evaluated at its maximum and P68 ( P95 ) is the probability density whose contour contains 68.3% (95.4%) of the data. (You might wonder where these extra significant figures come from to make this 68.3 and 95.4. They come from one-dimensional normal probability distributions. For a normal one-dimensional distribution, 68.3% of the probability is to be found in between one standard deviation (σ) less than the mean, and one standard deviation more than the mean while 95.4\% of the probability is to be found in between two standard deviations less than the mean, and two standard deviations more than the mean.)
Homework:
18.1: Estimate H0. To reduce dimensionality, in order to make things simpler, set ΩΛ=1−Ωm=0.7. Take M to be governed by the above prior. Use the Scolnic et al. (2018) data (available in 'supernova_data.txt') to make a contour plot in the H0,M plane.
18.2: Starting from the above P(H0,M|d), approximate the integral P(H0|d)=∫∞−∞dMP(H0,M|d) with a discrete sum and produce a plot of H0 vs. P(H0|d). Don't worry about the normalization of the probability density you plot.
18.3: Produce your own Ωm,ΩΛ 68\% and 95\% confidence contours using the Scolnic et al. (2018) data and, for simplicity, fixing M=-19.26 and H0=72.9 km/sec/Mpc. Ideally you would marginalize over these other variables, instead of fixing them, but that would be significantly more challenging. You can approximate the distributions as Gaussian (normal) for purposes of choosing the contour levels.


