1.23: Big Bang Nucleosynthesis - Predictions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Overview
Big Bang Nucleosynthesis (BBN) is the process by which light elements formed during the Big Bang. The agreement between predicted abundances and inferences from observations of primordial (pre-stellar) abundances is a major pillar of the theory of the hot big bang and reason we can speak with some confidence about events in the primordial plasma in the first few minutes of the expansion. Elements created at these very early times include Deuterium, Helium-3, Lithium-7, and, most abundantly, Helium-4. In this chapter we focus on the theory of Helium-4 production.
State of the art calculation of Helium-4 production in the Big Bang involves following a fairly large reaction network, between the various light elements in their thermal bath of photons and neutrinos. It is a sufficiently complicated calculation that it is done numerically on computers. Here we present analytic arguments that help us to understand why the results come out the way they do. This is a common situation in physics -- although perhaps not so common in physics as it is taught to undergraduates. Most problems are way too hard to solve analytically from first principles. Some problems are amenable to being solved numerically. When problems are solved numerically, we often want more than to just know the result of the calculation. We want to understand why the result is what it is. Such understanding is valuable for our own satisfaction, but also it often allows us to figure out, at least qualitatively, what the result will be if some assumption is changed. It is useful to be able to do this, rather than have to re-do the numerical calculation every time you get curious about the result of changing some input to the calculation.
In this chapter we present the results of numerical calculations of light element production in the big bang. We also provide analytic insight into why Helium production works out the way it does. We then use that analytic insight to understand how He-4 abundances are sensitive to conditions in the Big Bang.
With standard assumptions about the Big Bang, we find that about 25% of the mass that is in baryons ends up in Helium-4. In this chapter we will examine, as the basis of our analytic understanding of this result, the following sequence of events:
- At kBT≥0.8MeV, neutrons and protons are in chemical equilibrium.
- At kBT≃0.8MeV their ratio freezes-out at nnnp≃15.
- 4He production proceeds through the intermediate step of Deuterium (D) production, which is inhibited until kBT≃0.06MeV.
- At this temperature, nearly all neutrons end up in 4He, but by this point neutron decay has reduced nnnp from 15 to 17.
After presenting the story of Helium-4 production in the standard cosmological model, we discuss the sensitivity of the Helium-4 abundance to assumptions such as the value of Newton's constant, G.
Conditions prior to neutron-proton freeze-out
We begin by considering the universe at a time just prior to the BBN epoch, when the temperature of the universe is such that kBT≃ 10 MeV, much hotter, and denser, than it is today. At this time, the Universe is dominated by radiation, including paired relativistic particles like e− and e+ and ν and ˉν.
However, at this same time, baryon kinetic energies have dropped enough that they are nonrelativistic (kBT≪mpc2). The universe is still hot and dense enough to keep weak interactions such as these: n+νe⟷p+e−
n+e+⟷p+ˉνe
rapid. These reactions keep the neutrons and protons in chemical equilibrium with:
μn+μνe=μp+μe−
μn+μe+=μp+μˉνe
In kinetic equilibrium, electrons and positrons are at the same temperature, and they have the same masses. Also ne−≃ne+, which implies
μe−≃μe+
e−+e+⟷2γ reactions are fast, so μe++μe−=0
Using ??? and ???, we can therefore conclude that their chemical potentials are near zero. Similar arguments apply to neutrinos, although, we don’t have good evidence that nν=nˉν. However, in the standard cosmological model, we assume nν=nˉν, and hence conclude that μν=μˉν=0.
Box 1.23.1
Exercise 23.1.1: Based on the assumptions presented so far show that μn=μp.
Neutron-Proton Freeze-out
When the temperature drops to Tf, the critical temperature at which weak interactions are no longer fast, the neutron to proton ratio "freezes-out" to a nearly constant value. From the number density equations shown at the end of chapter 20 and from our previous result μn=μp, we can find the equilibrium ratio of neutrons to protons to be:
nnnp=(mnmp)3/2exp[−(mn−mp)c2kBTf]
Box 1.23.2
Exercise 23.2.1: You are given number density equations in chapter 20. Use them to derive Eq. ???. Assume that reactions ??? and ??? are fast.
After plugging in the known quantities and the correct freeze-out temperature (kbTf≈0.8MeV), this fraction evaluates to:
nnnp≃exp(−1.3MeV0.8MeV)≈15
where we have used the fact that mnmp≃1 and (mn−mp)c2=1.3 MeV. This ratio slowly drops over time due to neutron decay. Neutrons decay as n⟶p+e−+ˉν with t1/2=610s.
Nuclear Statistical Equilibrium
By the time the universe has cooled to kT≃0.3 MeV there is a sense in which all nuclear matter "wants" to be the bound state of 2 neutrons and 2 protons, helium-4, or 4He. But because the reactions necessary to create 4He are too slow, this does not happen for a while yet.
To explain what we mean by this "wanting" we introduce the concept of nuclear statistical equilibrium (NSE). NSE applies when all the reactions that can change the numbers of the different nuclei are sufficiently rapid. Here are some of these reactions, starting with one that forms deuterium, the bound state of a neutron and proton
p+n⟶D+γ
and then those that produce 3He
D+p⟶ 3He+γ
D+D⟶ 3He+n
those that produce 3H
D+D⟶ 3H+p 3He+n⟶ 3H+p
and those that produce 4He
D+D⟶ 4He+γ
3He+D⟶ 4He+p 3H+D⟶ 4He+n.
We could continue listing these reactions right through to the production of the very heaviest elements, but we'll stop here. If they, and their associated reverse reactions, were all happening sufficiently rapidly, then that creates a set of relationships between their chemical potentials. The result is that, just like we see with Eq. ??? their abundance ratios would only depend on their masses, the temperature, and the baryon-to-photon ratio. For a value of the baryon-to-photon ratio that appears to be consistent with our universe, the result is that, if NSE were to obtain, just about all the mass in baryons would be in 4-He once the temperature falls below kT≃ 0.3 MeV. As the universe cools further, the most abundant element switches from Helium to Carbon, and as it cools further it keeps switching to heavier and heavier elements. Well before we get to today's temperature, if NSE obtained the whole way, all the baryons in the universe would be in 56Ni, the nucleus with the highest per-baryon binding energy.
But this never happens, because the necessary reactions become slow, as we saw earlier, at temperatures as high as kT≃ 0.8 MeV. The main challenge to actually producing Helium-4 comes from the slowness of reaction ???, which is slow due to the small abundance of deuterium, which in turn is slow due to what we call "the deuterium bottleneck."
The Deuterium Bottleneck
The binding energy of a proton and neutron is ∼2.2MeV and thus we would expect that at the time when the universe has cooled to kBT≃2.2MeV we would begin to see deuterium. However, we don’t see deuterium in abundance until a much lower temperature of kBT≃0.06MeV. This is due to the massive dominance of photon densities over baryon densities and the high energy tail in their distribution. Even if only a very small percentage of photons has enough energy to break deuterium bonds, that small percentage can still correspond to a greater number density than the total number density of deuterons. These number densities do not become equal until around kBT≃0.06MeV. At this temperature enough Deuterium can form and survive for long enough to be converted into helium-4 by reaction ???. The deuterium bottleneck is broken.
Helium Production
Once the deuterium bottleneck is broken, Helium abundance can begin to move appreciably toward its very large NSE-desired abundance. The abundance of helium-4 increases until just about all of the available neutrons have been consumed. Without more neutrons, no more deuterium can be made, and there is once again no viable path for creating helium-4. Neutrons are thus the limiting fuel. Their abundance at kT=0.06 MeV can be used to approximately determine the final abundance of helium-4. That abundance has decreased some since neutron-proton freezeout since the age of the universe at that temperature is about 340 seconds and the half life of the neutron is about 610 seconds.
nnnp≃15exp(−340s×ln2610s)≃17
Some of the products of the reactions we listed above go on to form 7Li and others as well, but these account for only a very small fraction of the total baryonic mass.
Numerical evolution of the reaction network leads to the following predictions for primordial abundances relative to Hydrogen:
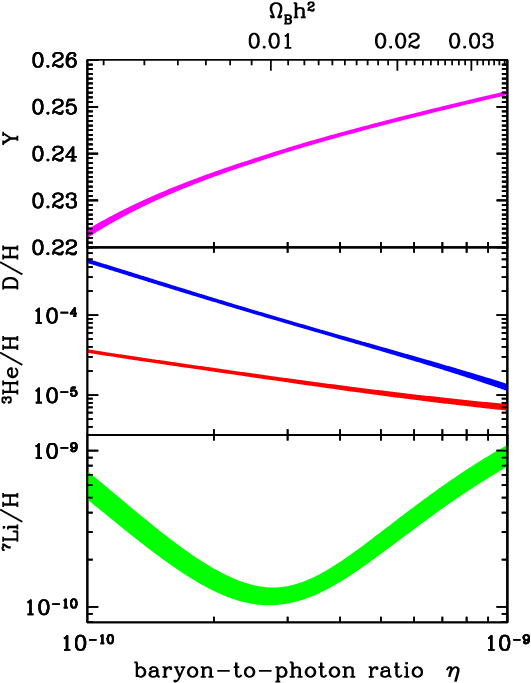
From the figure, we can ascertain some values for the primordial abundances of light elements. At a baryon-to-photon ratio value of η=(6.14±0.25)×10−10, we have abundance predictions of about:
DH≃2.75×10−5
3HeH≃9.28×10−6
7LiH≃3.82×10−10
These are all very small because essentially all neutrons go into creating 4He at 0.06MeV. Keeping this in mind, and using our (neutron-decayed) ratio of neutrons to protons, we can find Y, the fraction of baryonic mass in 4He:
Y=0.5×4mnNnmn(Nn+Np)=21+Np/Nn≃0.25=25%
where mn is the mass of a "nucleon" -- either a proton or neutron. The numerator here makes sense because the mass of helium-4 is about 4 mn and we get half a helium-4 for every neutron. The bottom is clearly the total baryonic mass, where the values for Nn and Np are to be understood as those just prior to formation of Helium-4.
Box 1.23.3
Exercise 23.3.1: Prove this percentage to yourself. From NnNp≃17, draw 2 rows, each with 7 protons and 1 neutron, each. Draw a circle containing both neutrons and 2 protons. This is a 4He nucleus. If mn≈mp, what percentage of your total mass is in the 4He nucleus?
Box 1.23.4
Exercise 23.4.1: Sketch a timeline with these two key BBN events in it: neutron-proton freeze-out and the end of the deuterium bottleneck. Label them and specify the temperature. Specify the ratio of neutrons to protons at both of these events. Why has the ratio decreased by the time of the later event?
Box 1.23.5
Exercise 23.5.1: If Newton's constant G were for some reason larger during BBN than it is today, the expansion rate at a given temperature would be higher (due to the Friedmann equation). Qualitatively, how would this impact predictions for Helium abudnance? Would Y, the fraction of baryonic mass in Helium, go up or down?


