4.5: Thermodynamics processes
( \newcommand{\kernel}{\mathrm{null}\,}\)
Isochoric
When the volume of a system remains constant during a thermodynamic process, the process is called isochoric. Consider a sealed container with a gas at equilibrium. If the sealed container is then heated, the gas particles will start moving around faster, exerting a greater pressure on the wall of the container. Setting the initial and According to Ideal Gas law, when the initial and final volumes are the same, we get the following relationship:
TiPi=TfPf
Since the volume stays constant, no work is being done and only the heat entering the system contributes to the change in internal energy. A physical example of this process is illustrated below, in addition to the PV diagram and the Energy-Interaction diagram that describes this particular process.
Figure 4.4.3: Example of an Isochoric Process.
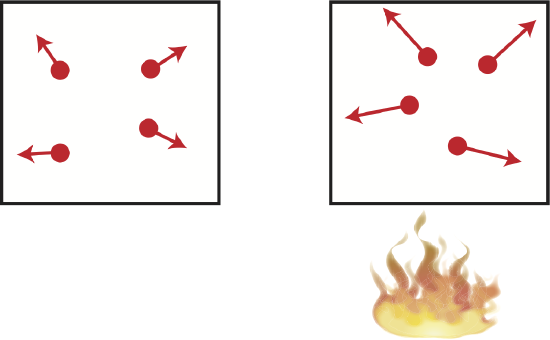
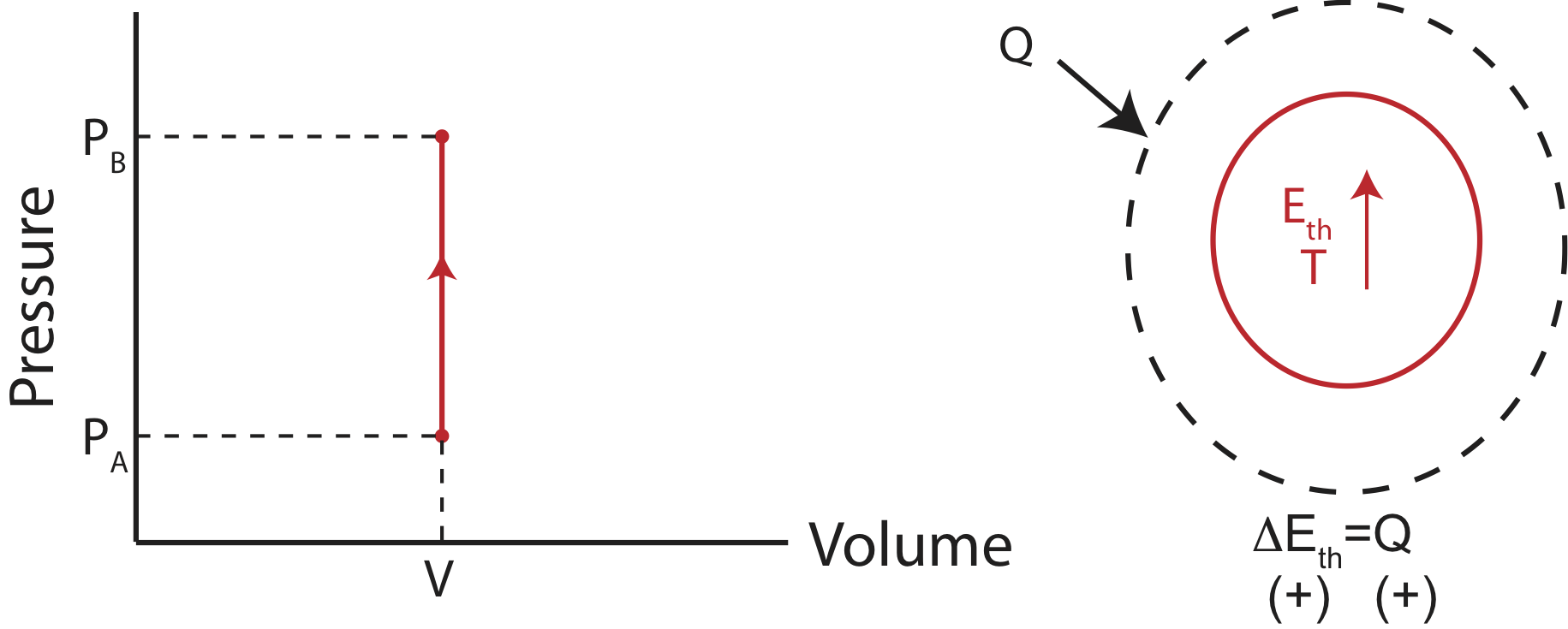
Using both the 1st Law and the Ideal Gas Law for an isochoric process, we find that heat depend on the change in pressure as:
Q=ΔEth=(total # of modes)12kBΔT=12(# of modes per particle)VΔP
Isobaric
Now imagine a different experimental set-up where the container has a movable piston or negligible mass and friction allowing the volume to change as the gas is either cooled or heated. As illustrated below when the gas is heated, the speed of the gas particles increases. This creates a larger pressure inside the container compared to the outside. The gas particles inside the container do work on the piston expanding the gas until the pressure outside and inside is the same, and the gas reaches equilibrium. Although, the particles are moving faster the volume is also larger, making it possible to have the same pressure as in its initial state. When the pressure of a system remains constant during a thermodynamic process, the process is called isobaric. And illustration of such process is shown below.
Figure 4.4.4: Example of an Isobaric Process.
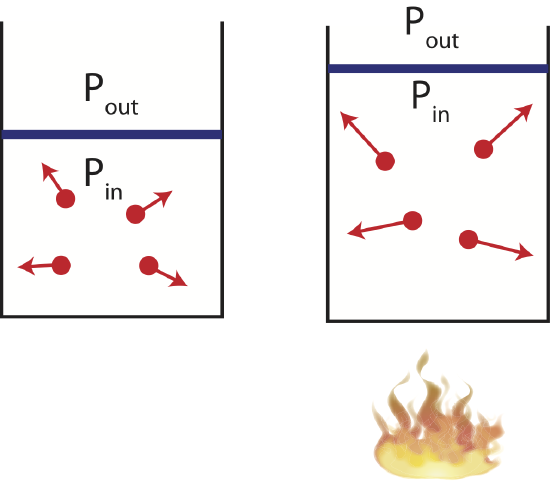
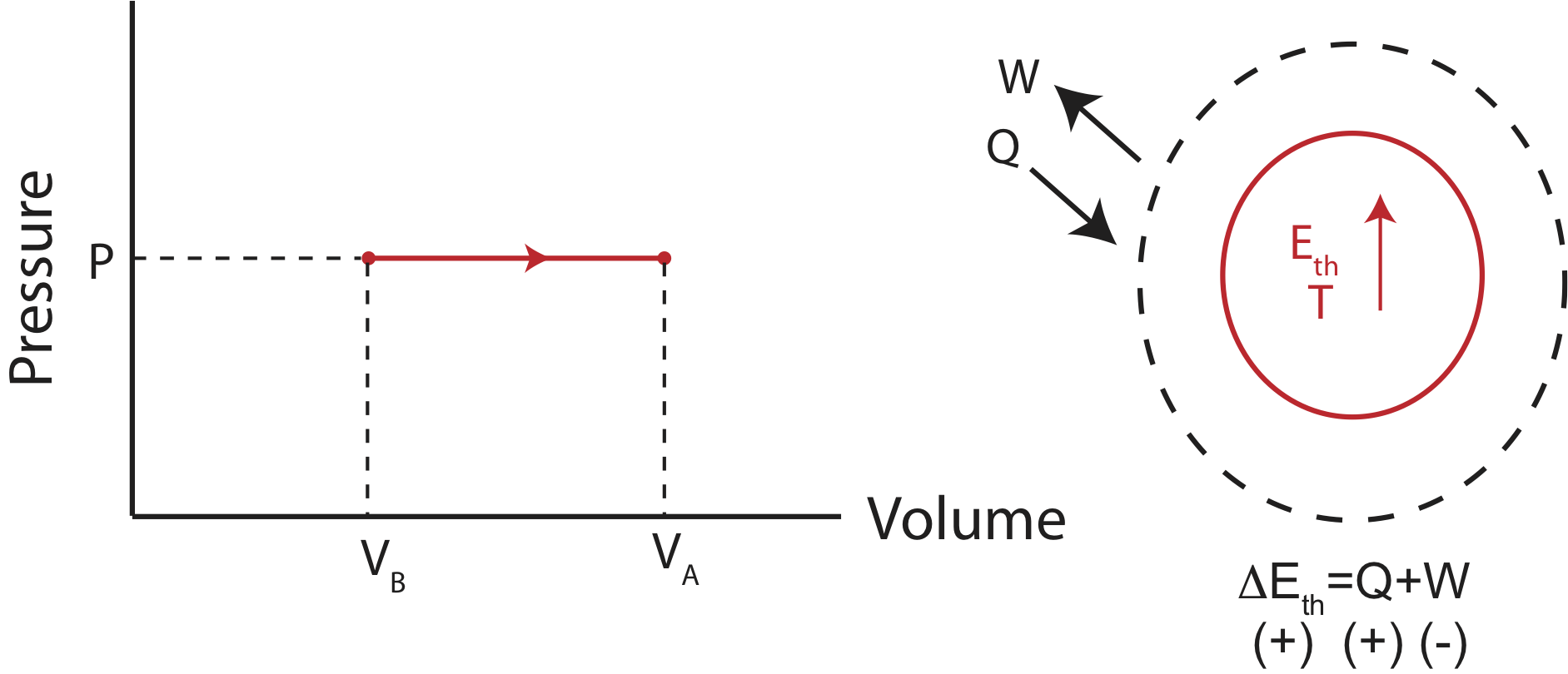
The corresponding PV diagram and the Energy-Interaction Diagram is also shown. Since the volume is increasing in this example, the work done is negative (the gas is doing work in the environment as it expands).
At constant pressure, calculating work is straightforward, since it is just an area of a rectangle, W=−PΔV. Therefore, the change in internal energy for an isobaric process is:
ΔU=Q−PΔV
Recall from above that we can define a new state variable as long as it depends on other state variable by some state function. Enthalpy is defined as:
H=U+PV
Note, that the three variables U, P, and V that define H are all state variable.
Why would a function equal to the internal energy plus the product of the two state variables pressure and volume be useful? As with energy, it is the changes in H that occur during a process that are important. Changes in enthalpy are most useful under certain conditions: specifically, situations in which pressure is held constant. Chemists and biologists conduct many of their experiments (any reaction carried out in a container open to the atmosphere) under constant pressure.
The following derivation shows why enthalpy is a convenient variable when considering changes occurring under constant pressure:
ΔH=ΔU+PΔV+VΔP
The last term is zero when the pressure is constant.
For ΔU we can substitute the expression for internal energy in Equation ??? we obtained from the first law of thermodynamics. This gives us
ΔH=Q−PΔV+PΔV=Q
So at constant pressure, the enthalpy change during a reaction is simply equal to the heat entering the system. Likewise, if a phase change is allowed to occur at constant pressure, the heats of melting and vaporization are simply equal to the changes in enthalpy. So now we finally see why heats of fusion and vaporization are often listed as changes in enthalpies. When you measure the energies transferred as heat during a phase change at constant pressure, you are directly measuring the change in the state function H. A negative ΔH means heat is transferred out, and the reaction is exothermic. A positive ΔH means heat is transferred in and the reaction is endothermic:
ΔH<0: exothermic
ΔH>0: endothermic
It is because ΔH=Q for the conditions so common in chemistry and biochemistry, and technology in general, that enthalpy is so useful. Most measurements are carried out at constant pressure, and for many systems, the only work involved comes from compressing or expanding a gas.
Example 4.5.3
Two moles of an ideal diatomic gas with vibrational modes frozen undergoes an isobaric process that results in a 2.5×10−3m3 change in volume and 500 Joules of work done on the gas. No phase change occurs during this process. Determine whether heat is zero, positive, or negative and if non-zero find its magnitude.
- Solution
-
Since work is being done on the gas, work is positive, and the change in volume must be negative. When the volume decreases at constant pressure, the temperature must decrease as well according to the Ideal Gas Law:
TiVi=TfVf
A decrease in temperature implies a decrease in internal energy. Since work is positive, in order to have ΔU<0, the heat must be negative according to ΔU=Q+W. To find heat, we first need to calculate the change in internal energy, Q=ΔU−W. Since there is not phase change ΔU=ΔEth. Thermal energy is proportional to change in temperature, which we can calculate from the ideal gas law:
ΔT=PΔVnR.
The quantity \(P\Delta V\=-W=-500 J), using the definition of work at constant pressure.
A diatomic gas with frozen vibrational modes will have 5 active modes (3 translational and 2 rotational kinetic energy modes). Using the equation for thermal energy:
ΔEth=(total # modes)12kBΔT=2NA×5×12kB−500J2R=−1250J
Solving for Q=−1250J−500J=−1750J.
Isothermal
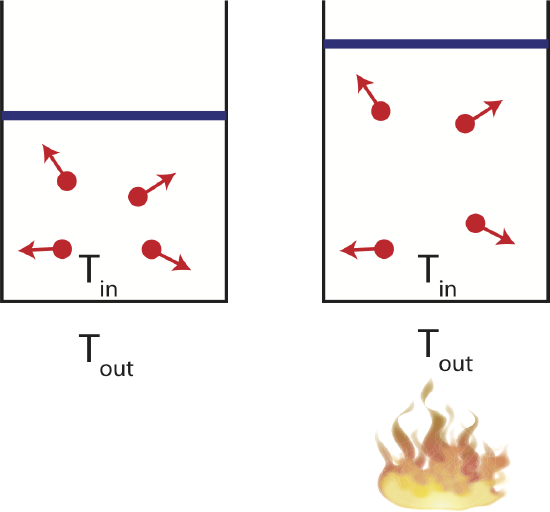
Consider a container in thermal equilibrium with a large reservoir which is kept at a constant temperature. If the system is in contact with a large temperature reservoir and the process occurs slowly, the system is always staying in equilibrium with its environment, keeping the temperature constant. In the figure below this implies that the temperature inside the container, Tin, will always equal to the temperature of the environment, Tout. This process is called isothermal. All the heat the enters the system which is free, the heat added will go into the work being done by the gas at it expands. Since the temperature of the gas does not change, the increasing volume will result in decreasing pressure, as seen on the figure below. Every point on the PV diagram is at the same temperature.
Figure 4.4.5: Example of an Isothermal Process.
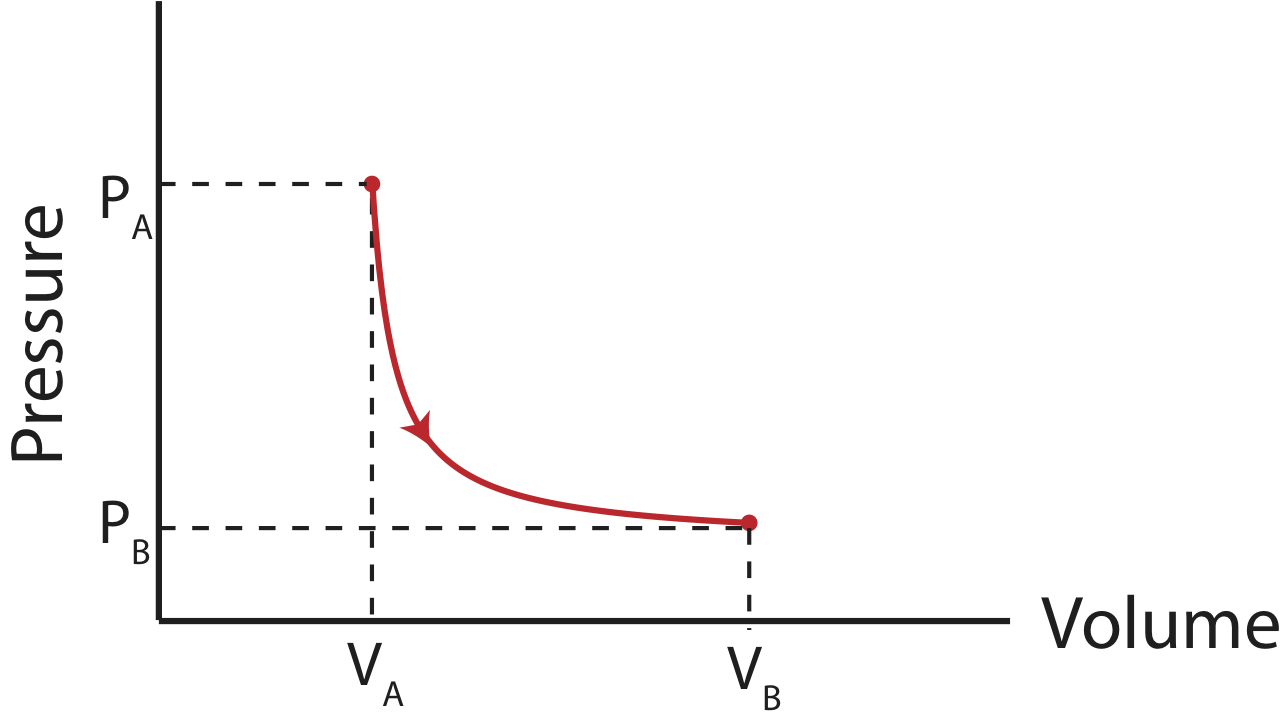
For an isothermal process, you can no longer simply calculate the area under the curve, so taking an integral is necessary:
W=−∫VBVAPdV=−∫VBVA(nRTV)dV=−nRT∫VBVAdVV=nRTln(VAVB)
There are many examples of isothermal processes that occur in systems that are built to regulate temperature. For example, in living cells temperature fluctuations are not desirable, so chemical reaction in cells occur isothermally. Also, many machines designed to keep the temperature constant, such as refrigerators or heat pumps, follow isothermal processes.
Adiabatic
Adiabatic processes cause an change in internal energy without transfer of heat, but purely through work. An example of a PV diagram and an Energy-Interaction diagram is shown below.
Figure 4.4.6: Example of an Adiabatic Process.
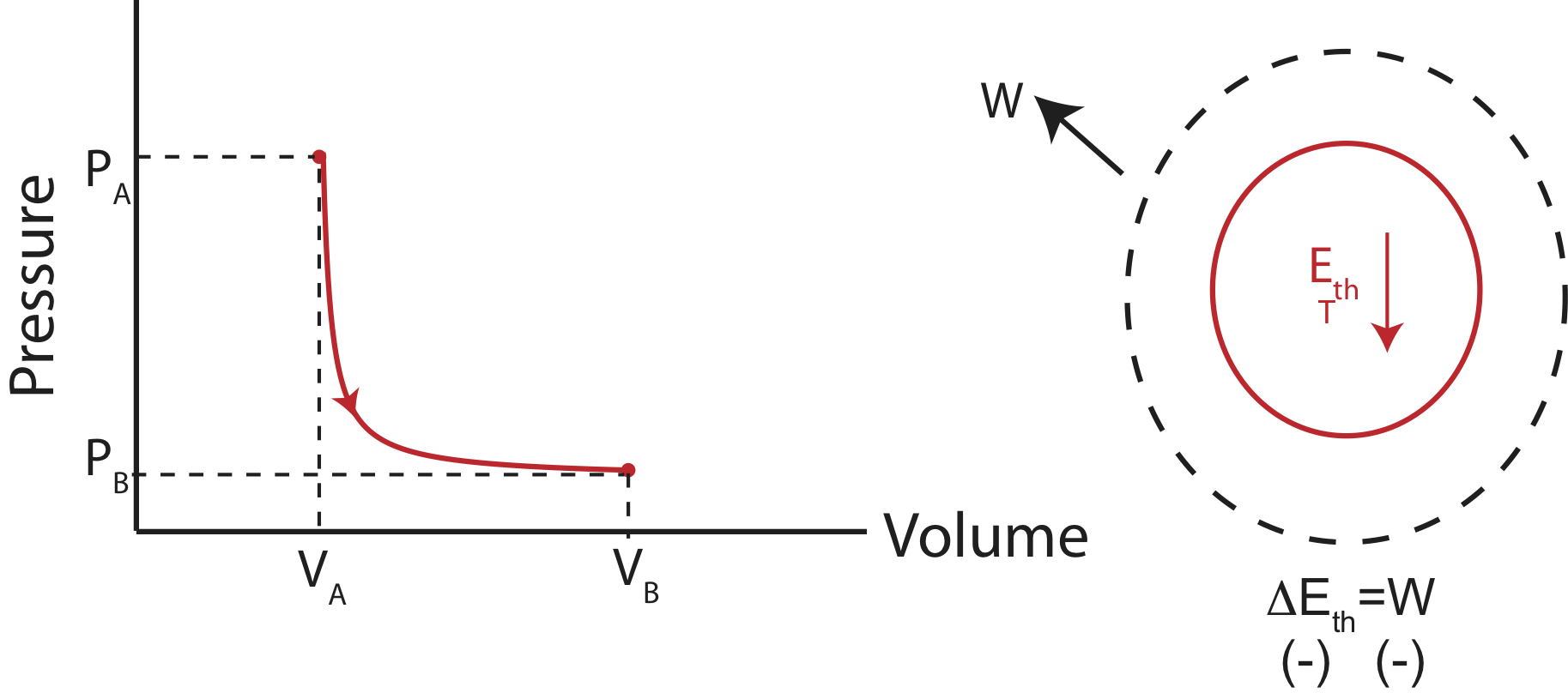
Adiabatic processes typically occur very quickly, such that the system has not time to exchange heat with its environment. Every time you open a carbonated beverage, the pressured gas quickly expands causing the temperature to drop. This adiabatic cooling cause the water vapor in the gas to condense, creating a small cloud. Another example in nature of an adiabatic process is the cooling of air in the mountains. As wind brings air over a mountain range, the lower pressure cause the air to expand, and thus cooling it. The cooling air often results in water vapor condensation creating clouds, causing it to rain. If there is a prevailing wind direction, this explains why on some mountain ranges there is more vegetation on only one side. By the time the cloud gets to the other side of the mountain, it has used up all of its moisture. Although, no processes are truly adiabatic (since they depend of an either perfectly insulated system or a process of a very quick time scale), often, it is a good approximation.
Alert
It is easy to confuse the idea of heat and temperature, but they are not the same thing. For an isothermal process, it is possible to add heat to a system, while keeping its temperature constant. Heat is the transfer of energy, and for an isothermal process all the heat that is added to the system goes into work done by the gas. It is also possible for a system to change temperature without any heat transfer, as seen in adiabatic processes. Temperature is an state variable that describes the internal energy (specifically, thermal energy) of the system. Internal energy can change if energy is transferred in or out of the system. But there are two ways to transfer energy, either with heat or work. Thus, work alone can change the temperature of a system.


