6.2: Engines and Thermal Efficiency
- Page ID
- 18480
A Simple Engine
Cyclic processes provide a means to have repeatable ways to convert heat energy that comes into the gas into work energy that leaves the gas. In order for heat to be exchanged, we know there must be a temperature difference, and a properly-designed device can run in a cycle to exploit a temperature difference to deliver useful mechanical energy. Such a device is called a heat engine. Of course, this requires a cyclic process that runs clockwise on the \(PV\) diagram. We will now examine the simplest version of an engine – one that forms a rectangle in its \(PV\) diagram. Our emphasis will be to visualize each leg of the cycle as a physical process involving a piston that is exchanging heat with a thermal reservoir and/or work with its surroundings.
Figure 6.2.1 – A Simple Engine

We'll start with what we already know about cycles – since the thermodynamic state returns to where it started, the internal energy doesn't change over the course of a cycle, which means that the work energy that comes out (equal to the area enclosed by the loop) equals the heat energy that goes in.
\[\Delta U = 0\;\;\;\Rightarrow\;\;\; Q_{in} = W_{out} = \left(P_2-P_1\right)\left(V_2-V_1\right) \]
We will now compute the heat transferred during all four individual legs of the cyclic process to confirm this result. As we do, we will include a diagram of what is happening physically.
Figure 6.2.2a – Process A–B

This is a quasi-static isobaric process, which involves heat being transferred into the gas slowly (from a thermal reservoir that's barely warmer than the engine gas at every step of the process). The temperature of the gas rises during the process, and the volume increases, while heat comes into the system. The amount of heat transferred is:
\[Q_{AB} = nC_P\Delta T_{AB} = nC_P\left(\dfrac{P_2\Delta V_{AB}}{nR}\right)=\left(\dfrac{C_P}{R}P_2\right)\left(V_2-V_1\right) \]
Figure 6.2.2b – Process B–C

This time we have an isochoric process, and since the pressure drops, it must be because the temperature is dropping. This can only occur with an unchanging volume when heat is leaving the system, and since the process is quasi-static, the temperature of the thermal reservoir is slightly lower than the temperature of the gas throughout the process. The heat lost during this stage is:
\[Q_{BC} = nC_V\Delta T_{BC} = nC_V\left(\dfrac{\Delta P_{BC}V_2}{nR}\right)=\left(\dfrac{C_V}{R}V_2\right)\left(P_1-P_2\right) \]
Figure 6.2.2c – Process C–D

This third leg is again an isobaric process, this time with the temperature and volume dropping. Again this quasi-static process requires that the temperature of the reservoir remain slightly lower than the temperature of the gas. The heat lost is:
\[Q_{CD} = nC_P\Delta T_{CD} = nC_P\left(\dfrac{P_2\Delta V_{CD}}{nR}\right)=\left(\dfrac{C_P}{R}P_1\right)\left(V_1-V_2\right) \]
Figure 6.2.2d – Process D–A

The final leg is again isochoric, and the pressure is increased along with the temperature by heat added from the thermal reservoir that is slightly warmer than the gas. The heat transferred is:
\[Q_{DA} = nC_V\Delta T_{DA} = nC_V\left(\dfrac{\Delta P_{DA}V_1}{nR}\right)=\left(\dfrac{C_V}{R}V_1\right)\left(P_2-P_1\right) \]
It is left as an algebra exercise to the reader to demonstrate that the sum of these four heat transfers equals the total heat transferred as given in Equation 6.2.1. When doing this exercise, it will be helpful to remember that \(C_P = C_V + R\).
Real-World Engines
Throughout the calculation above, it may have occurred to the reader that there was one awkward requirement kept coming up – the thermal reservoir must always be an infinitesimal amount different in temperature from the gas in the engine. How exactly does one accomplish such a feat? The reservoir is very slightly warmer, increasing the gas's temperature until they are at thermal equilibrium, then the reservoir gets a little warmer again, so that it can again give a small amount of heat to the gas, and so on? This process is obviously not something that can be reasonably engineered, and even if it could, the fact that the rate of heat flow is related to the temperature difference means that it would be painfully slow.
In the real world, we typically have two thermal reservoirs at fixed temperatures to work with – one at a high temperature from which the engine receives heat, and one at a low temperature, where the engine dumps heat. Notice that in the simple engine above, the gas had to both receive and dump heat, even though it received a net amount of heat that it converted into work. This turns out to be a required feature of all engines (for reasons we will explore later on) – an engine cannot simply take heat in from a single hot thermal reservoir and convert it into work in a cycle without also dumping heat into another, colder thermal reservoir. A schematic of this general principle of engines is shown below.
Figure 6.2.3 – Real-World Schematic of a Heat Engine

Many elements of the engine are featured in the schematic. First, the process must be cyclic, which means that the overall change in the internal energy is zero, and the overall heat that comes in (the heat in from the warmer reservoir minus the heat out to the cooler reservoir) equals the overall work that goes out (technically there is also work that comes in, but this schematic includes only the net work, while dividing the “in” heat from the “out” heat, for reasons that will soon become clear). We have included the heats exchanged with the two reservoirs in terms of their absolute values, so that we don't have to concern ourselves with heat in/heat out sign conventions. Clearly the work produced is the difference of the total heat energy that comes in from the hot reservoir minus the total heat energy that goes out to the cold thermal reservoir.
Thermal Efficiency
Now it is true that in the real world when we take heat from one reservoir and give some to another, colder one, we make the two reservoirs a little closer in temperature. Ideally, we would like to avoid “wasting” any of that outgoing heat energy that does nothing but increase the temperature of the colder reservoir, and instead just convert all of the heat energy coming from the hot reservoir directly into work. Achieving this goal would mean the creation of a “perfectly efficient engine,” and we would say that it has a thermal efficiency of 100%. Defining the percentage efficiency of any engine is therefore pretty obvious – simply take the ratio of the work extracted to the heat supplied:
It should be noted that the "work extracted" is the net work – the work that comes out during the full cycle minus the work that is put in (i.e. it is the area inside the closed loop in the clockwise PV diagram). Notice also that for this engine the temperature is not just slightly above the temperature of the gas in the engine, and in fact the force due to the gas pressure is not slightly greater than the external force when work is being done, either. So none of these processes are quasi-static. But as we have seen, this will not stop us from making good use of the quasi-static process models.
We will see later that engines are maximally efficient when the processes they follow are reversible, but of course this requires for some processes that the thermal reservoir involved varies its temperature to remain infinitesimally larger or smaller than the temperature of the engine. This contradicts the entire notion of a "thermal reservoir," so it is clear that real engine efficiencies will be worse than those of reversible engines we may use to model them. Still, we can use the ratio of total work out to total heat in for a reversible model to compute the maximum possible efficiency for the engine modeled.
Example \(\PageIndex{1}\)
In the cyclic process for an engine shown below, the process from A to B triples the pressure, the process from B to C is adiabatic, and the working gas in the engine is monatomic. Compute the maximum thermal efficiency of this engine.

- Solution
-
Let's call the volume of the gas during the isochoric leg (\(A\rightarrow B\)) \(V_o\). We can use the adiabatic process to relate the volume the gas occupies at C to \(V_o\):
\[PV^{\gamma} = const \;\;\;\Rightarrow\;\;\; \left(3P_o\right)V_o^{\frac{5}{3}} = \left(P_o\right)V_C^{\frac{5}{3}} \;\;\;\Rightarrow\;\;\; V_C=3^{\frac{3}{5}}V_o\nonumber\]
The total area in the loop (the net work done in the cycle) is the area under the adiabat plus the (negative) area under the isobar. We have both of these quantities in terms of the pressures and volumes:
\[\left. \begin{array}{l} \text{adiabat:} && W_1=\dfrac{1}{1-\gamma}\left[P_fV_f-P_iV_i\right] = \frac{3}{2}\left[3P_oV_o-P_o\left(3^{\frac{3}{5}}V_o\right)\right] = 1.600P_oV_o \\ \text{isobar:} && W_1= P\Delta V = P_o\left[V_o-\left(3^{\frac{3}{5}}V_o\right)\right] = -0.933P_oV_o \end{array}\right\}\;\;\;\Rightarrow\;\;\; W_{net}=W_1+W_2 = 0.667P_oV_o\nonumber\]
Heat exits the system during the isobaric process, and no heat is exchanged during the adiabatic process, so all the heat that comes into the engine does so during the isochoric process, and this is easy to compute for a monatomic ideal gas:
\[Q_{in} = \frac{3}{2}\Delta P V = 3P_oV_o \nonumber\]
The efficiency comes from the ratio of net work out to heat in:
\[e = \dfrac{W_{net}}{Q_{in}} = \dfrac{0.667P_oV_o}{3P_oV_o} = 22.2\% \nonumber\]
Otto Cycle
Our most recognizable type of engine is the internal combustion engine, and the most common cyclic process these follow is called the Otto cycle.
Alert
In what follows, when the word “gas” refers to the gas within the piston, which is mostly air. When referring to gasoline (the most common combustion fuel), we will refer to it in that long form – we will not use the shortened version of “gas."
We'll start by putting up a \(PV\) diagram that approximates the process, then explain each leg of the cycle.
Figure 6.2.4 – The Otto Cycle

process A-B (adiabatic compression)
Gasoline (or other combustible) vapor enters the chamber and mixes with air at a cool (ambient) temperature, at which point work is done on the mix to compress it. This happens very fast, so that the gas has no time to exchange heat with the surroundings, and this prompts us to treat this process as adiabatic.
process B-C (isochoric heating)
The gasoline is ignited, which rapidly changes the temperature of the gas inside the piston. Technically, the heat is not coming from outside the engine, but rather it comes from an exothermal chemical process, but it amounts to the same thing. This ignition happens very suddenly, before the gas has time to expand the piston, so we treat this process as isochoric.
process C-D (adiabatic expansion)
The heated gas is now at a very high pressure, and this pressure expands the piston, doing work. Once again, the speed of this process is so great that very little heat has time to escape the piston as it occurs, so we treat this process as adiabatic.
process D-A (isochoric cooling)
After fully expanding, the cooled-but-still-hotter-than-ambient gas is expelled from the engine, and a new load of air and gasoline vapor enters the chamber. Technically the gas doesn’t “cool isochorically,” but this amounts to the same thing, as the chamber is soon filled with new gas at a lower temperature and at the same volume.
This example shows how we can make use of what we have learned about thermodynamic processes to analyze real-world situations, even though our understanding is based on ideal situations that don’t exist in the real world. We simply look at the features of the real-world process, and match it as closely as possible to a quasi-static process. During this “matching” process, we take care that the endpoints match correctly (because those are equilibrium states), and that the heat/work transferred during the process makes sense. In the above example, this consisted of asking if the process occurred fast (no time for heat to flow) or if the volume didn’t change (no work done). We’ll see another form of this matching again shortly.
Let’s look at the efficiency of this cycle. Keep in mind that our idealized version will be more efficient than what we are able to achieve in the real world, but this gives us an upper-limit on what we can hope for. To get the efficiency, we need the heat supplied by the hot reservoir and the heat taken by the cold reservoir. In this cycle, heat exchanges only occur during processes B-C and D-A, which are both isochoric, so the heat exchanges are proportional to the temperature changes. The efficiency is therefore given by:
It should be clear from this result that the engine runs more efficiently when the temperature difference between the two thermal reservoirs is greater. In this case, that is the difference between the temperature of the injected gas and the ignited gas. It should be clear from the diagram that this difference can be measured in terms of the difference between (or more correctly, the ratio of) the two volumes the gas occupies. In practical terms, the gas cannot be squeezed to as small of a volume as one wants before igniting it, because the rise in temperature due to the compression can itself spontaneously ignite the gas. Higher octane fuels allow for greater compression without this unwanted spontaneous ignition, improving efficiency.
As we can infer from above, it is possible to rewrite the efficiency of this engine in terms of a variable that we can measure more easily than the temperatures – namely a property of the engine itself. Two of the four processes are isochoric, which means that the volume only changes twice during the whole cycle, which means we have only two volumes to worry about – the maximum and the minimum. The maximum occurs when the piston is completely expanded, and the minimum when it is completely compressed. We don’t even really care what these values are when it comes to efficiency, but rather all we care about is the ratio of these volumes, which is called the compression ratio:
\[r = \dfrac{V_{max}}{V_{min}} = \dfrac{V_{A\;or\;D}}{V_{B\;or\;C}}\]
We have a relation between the temperature and the volume along the path of an adiabat, which gives:
Plugging the Equation 6.29 into Equation 6.27 results in the following equation for the efficiency of this cycle for a given compression ratio:
\[e=1-r^{1-\gamma}\]
Diesel Cycle
With a small alteration to the Otto cycle, the efficiency can be improved somewhat. This alteration consists of controlling the ignition process so that it occurs at a constant pressure rather than a constant volume. This engine design uses what is called the diesel cycle. This of course means that the ignition has to occur less "explosively," which reduces the rate at which the cycle can occur, and we know from Physics 9A that the rate at which work is output is the power of the cycle, so while this cycle comes out to be more efficient, it provides less power.
To determine the efficiency difference, one needs only to change the denominator of Equation 6.2.7, which accounts for the ignition process (from B to C). Instead of occurring at constant volume, it occurs at constant pressure, which simply changes the \(C_V\) to \(C_P\), giving:
\[e = 1-\dfrac{C_V\left(T_D-T_A\right)}{C_P\left(T_C-T_B\right)}=1-\dfrac{1}{\gamma}\;\dfrac{T_D-T_A}{T_C-T_B}\]
The term that subtracts from the efficiency is lowered by a factor of gamma, resulting in higher efficiency. In addition, higher compression ratios are possible, because the air is compressed without the fuel present (the fuel is added gradually using fuel injectors during the ignition process, keeping the pressure constant), removing the problem of the fuel igniting during compression. Of course, while this process was exclusive to diesel engines many years ago, nowadays fuel injection and its accompanying higher compression ratios are standard in gasoline-burning automobiles.
Carnot Cycle
We were able to cleverly describe the Otto and diesel cycles in terms of 4 quasi-static processes, by treating the ignition of a gas as if heat is added rather than coming from a chemical reaction, and by treating replacement of gas as if heat is expelled. Without these tricks, keeping these processes quasi-static would make them very slow, and could not happen between reservoirs of two fixed temperatures, as shown in Figure 6.2.3, because for a process involving heat transfer and temperature change (which is the case for both isochoric and isobaric processes) to occur quasi-statically, the reservoir must change temperature to remain only infinitesimally different from the temperature of the gas. We can't get something for nothing, and in fact both the ignition and gas replacement processes are irreversible, making these processes only approximately the quasi-static cycles we declared them to be.
From this analysis, we see that the problem with including isochoric and isobaric processes in the "real world" case of an engine constrained to function between two reservoirs with fixed temperatures is that we can't make these processes reversible. But even under this fixed-temperature constraint on the reservoirs, there are two processes we can (in principle) perform quasi-statically. The adiabatic process involves not heat transfer at all, so the relative temperature of the engine and the reservoir is not relevant. The isothermal process leaves the temperature of the engine fixed, so if it happens to equal the temperature of the reservoir, there is no problem.
In the discussion that followed Equation 5.8.20, we noted that at any given point on a PV diagram for a gas, the adiabat that passes through that point is steeper than the isotherm that also passes through it. Because of this, we can create a cyclic process that utilizes two isothermal processes (one on the top, one on the bottom of the PV diagram) and two adiabatic processes (one on each side of the PV diagram), and this cycle can be driven by two fixed-temperature reservoirs. This is known as the Carnot cycle.
Figure 6.2.5 – The Carnot Cycle

We can compute the efficiency of this engine as we did with the Otto and diesel cycles. Noting that there is no heat transferred during the two adiabatic processes, and using Equation 5.8.16 for the heat transferred during the two isothermal processes, we have:
\[ \left. \begin{array}{l} \left|Q_H\right| = W_{out} = nRT_H\ln\left[\dfrac{V_B}{V_A}\right] \\ \left|Q_C\right| = -W_{in} = -nRT_C\ln\left[\dfrac{V_D}{V_C}\right]=nRT_C\ln\left[\dfrac{V_C}{V_D}\right] \\ e = 1 - \dfrac{\left|Q_C\right|}{\left|Q_H\right|} \end{array} \right\} \;\;\;\Rightarrow\;\;\; e = 1-\dfrac{T_C}{T_H}\dfrac{\ln\left[\dfrac{V_C}{V_D}\right]}{\ln\left[\dfrac{V_B}{V_A}\right]}\]
There is more we can do here, however. The volume of state B is related to the volume of state C by virtue of being on the same adiabat (the same is true of states D and A). Thus:
\[TV^{\gamma - 1} = const\;\;\;\Rightarrow\;\;\;\left\{\begin{array}{l} T_HV_B^{\gamma-1}=T_CV_C^{\gamma-1} \\ T_CV_D^{\gamma-1}=T_HV_A^{\gamma-1} \end{array} \right\} \;\;\;\Rightarrow\;\;\; \dfrac{V_B}{V_A} = \dfrac{V_C}{V_D}\]
Plugging these in above has the logarithms in the numerator and denominator cancelling, making the efficiency of a Carnot cycle a simple function of the temperatures of the two reservoirs:
\[e=1-\dfrac{T_C}{T_H} \]
The greater the temperature difference is between the two reservoirs, the greater the efficiency of the Carnot engine.
Refrigerators
One thing we have seen consistently in our discussion of engines is that the cycles are clockwise on the PV diagram. This ensures that after a full cycle work comes out of the system as heat goes in. What happens if we run the cycle in reverse? Then work goes in and heat comes out. This is the basis of a refrigerator. Naturally this doesn’t mean that we can take an internal combustion engine, put it in “reverse,” and it turns into an air-conditioner. For one thing, we can’t “un-ignite” the gas. But we can perform the processes in the opposite direction by other means. First, let’s look at a schematic for a refrigerator, as we did for a heat engine:
Figure 6.2.6 – Real-World Schematic of a Refrigerator
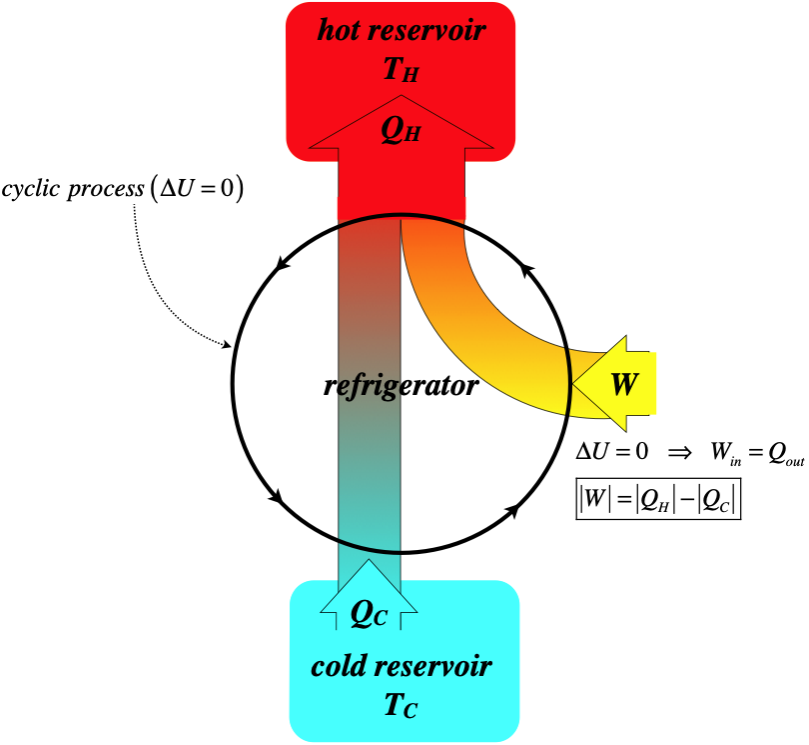
The efficiency of a refrigerator is not defined in the same way as an engine, since the goal here is to remove as much heat as possible from the cold reservoir while putting in as little work as possible. We therefore define the coefficient of performance as the ratio of the heat removed to the work required:
\[K=\dfrac{\left|Q_C\right|}{W}=\dfrac{\left|Q_C\right|}{\left|Q_H\right|-\left|Q_C\right|}\]
An extremely-simplified way to think about how a refrigerator works is this: We know that if we very suddenly compress a gas, it gets much hotter (see the example at the very end of Section 5.8). Unsurprisingly, the reverse is also true: Allowing a gas to suddenly expand a piston results in the gas cooling greatly. Suppose we want to make the interior of a refrigerator cooler than the exterior (duh, that's the definition of a refrigerator!). Start with a gas in a piston outside the refrigerator, and compress it to a small volume, and wait with it compressed until it comes to the outside temperature. Then release the piston suddenly and quickly carry it into the refrigerator. If we compressed it enough, the temperature change of the gas in the piston will bring its temperature below that of the interior of the refrigerator. We wait a little while, as the interior of the refrigerator surrenders heat to the cold air in the piston, thereby cooling the air within the refrigerator. When these reach equilibrium, we carry the piston back outside, and repeat the process. This transports thermal energy out of the refrigerator.
The work done on the gas during compression exceeds the work done by the gas during expansion (i.e. net work needs to be put in). The compression and expansion processes are adiabatic, while the "waiting" processes are isochoric, which gives a PV diagram that looks something like this:
Figure 6.2.7 – PV Diagram of a Simple Refrigerator

Obviously we sacrificed a lot of reality for this easy-to-understand "refrigerator." We obviously don't need to transport the piston in and out of the refrigerated chamber, and can instead pipe the gas into and out of it, compressing it as it leaves, and expanding it as it enters. But there is still a fairly big problem with this design. In order for heat to be transferred in the proper directions at the proper times, we need the temperature of the gas after it cools from expansion to be lower than the ambient temperature in the refrigerator. On the PV diagram, the temperatures inside and outside the refrigerators correspond more-or-less to the temperatures of states B and D, respectively. This means that if we draw isotherms through points B and D, that the gap between those isotherms represents the maximum temperature gap we can maintain between the hot and cold regions. Obviously this is a function of the pressure difference we can create between the compressed gas and the expanded gas, but in practical terms, this is a substantial obstacle.
The way this limitation is overcome is to carry much of the thermal energy in the phase of the refrigerant. We know that we can change phases by combinations of compressing/expanding and heating/cooling the fluid, and the latent heat of vaporization is substantial compared to the specific heat capacity for a small temperature change. This leads to this basic process:
- the compressor changes the phase of the refrigerant into liquid, which warms it above the outside temperature
- the fluid then enters a condenser coil, which has the purpose of increasing the contact area with the outside air, speeding up the process of dumping heat
- by the time the fluid has passed through the condenser coil, it is at a high pressure, but has come to thermal equilibrium with the outside air, and it then passes into an expansion valve, where it expands adiabatically, changing phase back to gas and dropping significantly in temperature, below the temperature of the inside air
- the gas then passes through an evaporator coil, which increases the rate as which the heat can enter the refrigerant from the inside air, and at the end of the evaporator coil, it reenters the compressor to start the cycle again.


