5.1: Temperature
( \newcommand{\kernel}{\mathrm{null}\,}\)
Thermal Energy
Back in Physics 9A, the idea of thermal energy first arose in the context of energy conservation. We concluded that work done by non-conservative forces would convert mechanical energy into this form of energy, which became internal to the system, and didn't spontaneously return to mechanical form. We know intuitively that this form of energy reveals itself to our senses through temperature. We also can intuit that two objects at different temperatures that are brought into contact can exchange energy and change their temperatures (cold milk added to hot coffee both cools the coffee and warms the milk).
It therefore makes sense that we begin our exploration of this topic by examining the concept and the measurement of temperature, but before we do, two definitions are in order:
thermal contact: when two systems are allowed to directly exchange thermal energy with each other
thermal equilibrium: when two systems in thermal contact nevertheless exchange zero net thermal energy
Zeroth Law of Thermodynamics
Imagine the following scenario: Three systems, which we will call A, B, and C, are arranged as shown in the left figure below (in thermal contact), exchanging thermal energy. They are allowed to continue this until systems A and B are in thermal equilibrium, while systems B and C are also in thermal equilibrium. The question is, after these equilibria are reached (the middle figure), if system A and C are brought into thermal contact (the right figure), will they automatically be in thermal equilibrium?
Figure 5.1.1 – Thermal Equilibrium Thought Experiment
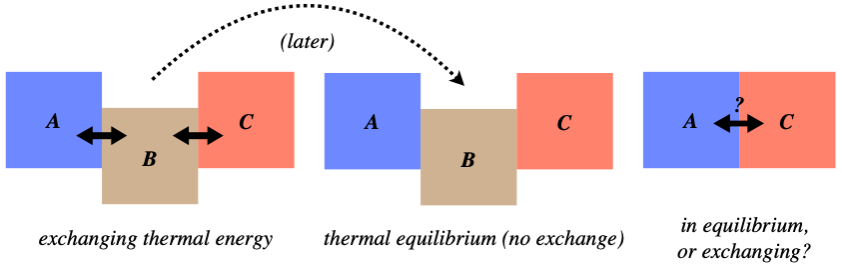
We won't beat around the bush on this – the answer is "yes." While worded in the arcane language of physics with all the references to thermal equilibrium, the answer is fairly obvious when worded differently: When two systems come to thermal equilibrium, they have reached the same temperature, and when two systems that have the same temperature come into contact, no thermal energy is exchanged between them. That is, we don't see one of them get spontaneously hotter than the equilibrium temperature while the other gets cooler than the same temperature.
The key thing to take away from this is that temperature is an indicator of whether a thermal transfer will spontaneously occur between two systems in thermal contact. We know this is true intuitively, and this fact explains the peculiar name of this law. Back in the 19th century when thermodynamics was being developed, the first and second laws of thermodynamics were expressed. In the 20th century there was a somewhat more rigorous treatment of the subject, and physicists realized that for completeness one should probably state that a property that we call “temperature” exists and can be uniquely defined. They didn’t feel like it was a good idea to make this a later law in the queue (there were three laws of thermodynamics by then, and in the 60’s another principle was dubbed the fourth law), so they went backwards to zero.
To co-opt a famous phrase from Supreme Court Justice Potter Stewart in 1964, temperature is not easy to define, but when it comes to determining if one thing is hotter than another, you know it when you see it. What this means is that temperature has many easily-measurable consequences in the physical world, and we can define temperature in a relative sense in terms of those consequences. We will see exactly how we do this now, and in fact we will even come up with a clever way of defining it in an absolute sense (i.e. we will not have to compare temperatures).
Relative Temperature Scales
When it comes to defining a temperature scale, the fact that (for now) we are only interested in differences means that we can set our scale arbitrarily. One way to do this is to pick a phenomenon that we can refer to as our reference. One phenomenon that we know is related to temperature is phase changes. We commonly see water in all three of its phases – ice, liquid water, and steam – and water is the most abundant substance on the surface of our planet, so it seems like a good choice. We know that it freezes at some low temperature and boils at some high temperature (well, we are actually defining temperature such that it is lower when water freezes than when it boils). Therefore we can arbitrarily set temperature equal to zero degrees at the freezing point, and set it equal to 7.5 degrees at the boiling point. We can then write these melting and boiling points as 0ºW and 7.5ºW. On this scale, the standard temperature of a healthy human body is 2.775ºW. This is not a very compelling scale, and one that makes more sense is the celsius (or centigrade) scale, which divides the temperature from water freezing to boiling into 100 equal degrees, starting at zero for freezing. Another is the fahrenheit scale, which starts at 32ºF for freezing and 212ºF for boiling.
Digression: Give the Fahrenheit Some Love!
It may seem like the fahrenheit scale is incredibly arbitrary, but in fact it has many practical advantages over the celsius scale. These advantages are decidedly “human” in nature. Our ability to sense temperature differences is pretty sensitive (depending upon many factors), so having more degrees between two close temperatures provides us a level of precision that is easier to relate to (without having to resort to more decimal places). This is especially important if we are reading the temperature off a device (thermometer) that has only whole number gradations. Another human element is that the fahrenheit scale reserves 0º and 100º for (more-or-less) the extremes of human experience (at least in a cold northern climate, like where the German physicist Daniel Gabriel Fahrenheit lived). And there is one other nice feature, which interestingly is related to the advantage of using degrees instead of radians when measuring angles. The circle is divided into 360 degrees so that one can subdivide it an enormous number of ways, while still making the angle observable – 360 has prime factors of: 23×32×5. Well, the number of subdivisions of the Fahrenheit scale from freezing to boiling water is also very high, since the difference is 180ºF. In a time before calculators, such advantages were always welcome.
We have two points on our temperature scale that we can measure (using water), and these two points define the line that is our scale, but the question arises, “How do we measure the temperatures between the freezing point and the boiling point (and the temperatures beyond them in both directions)?” We do this not by measuring temperature directly, but rather by measuring the effects of temperature changes. We will look at a few of these effects, and how they can be used to fashion a thermometer.
Gas Thermometers and the Absolute Temperature Scale
The first effect we will look at is how temperature changes cause changes in pressure in a gas (assuming that everything else is held fixed). Suppose we perform an experiment where we measure the pressure of a gas for many temperatures (but a fixed volume) and graph the results. We find that the relationship is linear, but the graphs of different gases (or different volumes of the same gas) have different slopes. When this was first analyzed, the technology was not available to bring the temperatures down extremely low, but extending these graphs reveals the remarkable result that when the pressure hits zero, all the graphs hit the axis at the same point!
Figure 5.1.2 – Extrapolating Absolute Zero
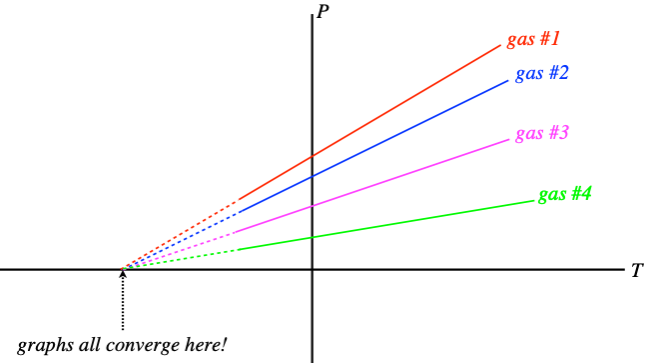
What this suggests is that we can redefine the zero point for temperature, and it will hold for all gases in all circumstances – an absolute scale is born! All that remains is to determine what temperature differences between neighboring integers should be used, and Celsius was the choice. So essentially the absolute temperature scale (a unit of measurement called kelvins, no “degrees”) is the same as Celsius, with the zero point shifted backward. How far? 0oC≈+273.15K.
Notice that this result also provides us an opportunity to simply relate pressures and temperatures of a gas in a confined volume. Re-drawing the P vs. T graph with the T axis measured in kelvins, we get a line that intercepts the origin:
Figure 5.1.3 – Gay-Lussac's Law
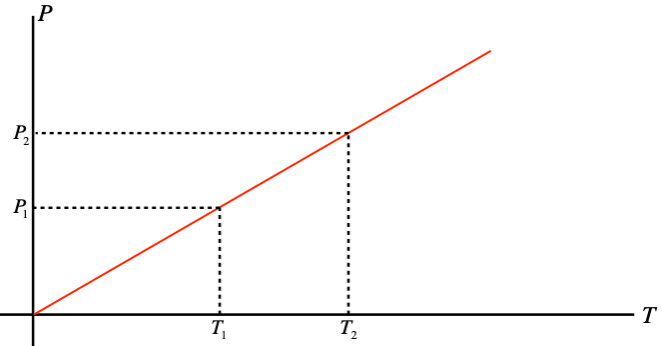
Using similar triangles, we can immediately derive a relationship between pressures and temperatures for gases confined to a fixed volume:
P1T1=P2T2⇒P1P2=T1T2


