3.4: Electricity and Magnetism

Motion in E&M

Electricity and magnetism was the main wildly-successful theory at the time that Einstein came onto the scene. Maxwell had shown how the two different forces could be unified into one mathematical theory. Electric charges cause both electric and magnetic fields, both of the fields exert forces on electric charges (in different ways), and each of the two fields (when they vary in time) can induce the existence of the other.

But when Einstein pondered his ideas about relative motion, an important question came to mind. The velocity of an electric charge appears in two different places in Maxwell's theory: A moving charge produces a magnetic field that is proportional to its speed, and a moving charge experiences a force from an external magnetic field that is proportional to its speed. So the obvious question to ask is, "What happens if we just view the moving charge from a frame that is stationary relative to the charge?" In this frame, it would seem that there is no magnetic field produced by the charge, and this charge would experience no force from an external magnetic field. Reconciling this is vital to confirming the validity of both theories, and we will do so with – what else? – a thought experiment.

Lorentz Force in Two Frames

Let us consider the following simple example from Physics 9C:

Figure 3.4.1 – Ann Observes a Stationary Charge Near a Current-Carrying Wire

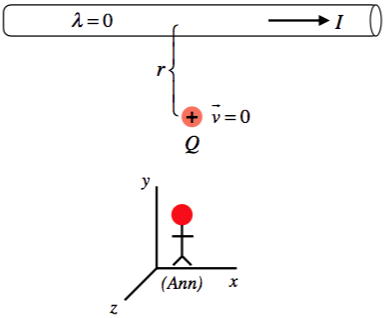
Ann observes a positive point charge \(Q\) that is at rest in her inertial frame. Close by (a distance \(r\) away), parallel to the \(x\)-axis, is a long-straight wire that carries a current \(I\) in the \(+x\)-direction. Like any other current-carrying wire, this one has zero electric charge density. It should be immediately clear that Ann will witness no net force on this charge – there is no charge density on the wire to produce an electric field, and although the current produces a magnetic field at the position of the charge, the charge isn't moving, so there is no magnetic force on it either.

Okay, all simple stuff. We continue with our thought experiment as we usually do, by considering what is seen by a different observer, Bob. Recall that electric current is typically due to movement of electrons in a conductor (while the protons remain stationary), and these electrons, being negatively-charged move in the direction opposite to the electric current. So for our thought experiment, let's choose Bob to be an observer in a frame that moves along with the electrons in the conductor:

Figure 3.4.2 – Bob Moves by the Charge with the Electrons

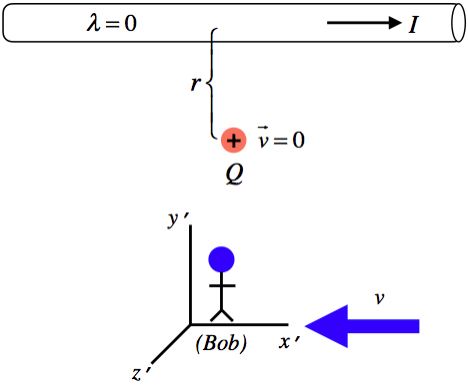
At first blush, it might seem that Bob should see a magnetic force on the charge, because according to him, the electric charge is moving in the magnetic field of the wire. Specifically, the right-hand-rule tells us that the magnetic field of the current points into the page at the position of the charge, and the charge (according to Bob) is moving to the right. So applying the RHR for the Lorentz force \(\vec F=Q\vec v\times\vec B\), we find that the force on this positive charge must be toward the wire. But if this force exists, then Bob would see the charge start moving closer to the wire, while Ann would see the charge remain stationary. Both of these results cannot be true, so what are we missing?

To answer this, we need to have a closer look at the charges that comprise the electric current. We have set things up so that Ann is stationary relative to the protons (with the electrons moving left at \(v\)), and Bob is stationary relative to the electrons, which means that relative to him, the protons are moving to the right at a speed \(v\). At the start of our thought experiment, we said that Ann witnesses zero charge density on the wire. This is because the electrons provide a negative charge density that is equal in magnitude to the positive charge density provided by the protons. These densities are determined by the spacings of the charges – the closer together they are, the more dense the charge distribution is. But relative motions changes distances with length contraction, so Bob will not measure the charge separations to be the same that Ann measures.

Figure 3.4.3 – Comparing Charge Densities Measured

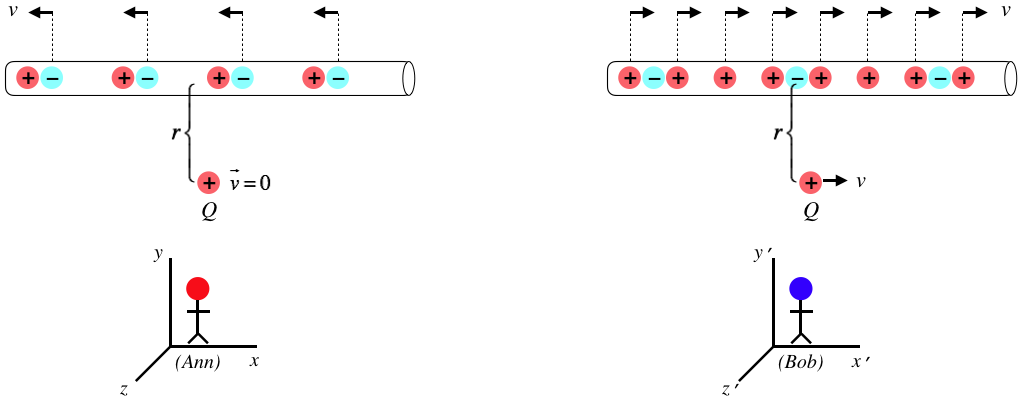
Here we see side-by side the views of each observer in their rest frames. The electrons are moving relative to Ann, so to her their separation is length-contracted. In Bob's frame their separations are not length-contracted, so he see them to be farther apart. Similarly, the protons are moving in Bob's frame, and stationary in Ann's so Bob sees them to be closer together than Ann. The end result is that while Ann sees zero charge density on the wire, Bob does not, because he sees the protons much more closely-spaced than the electrons. Interestingly, both observers see an electric current going to the right (positive charges to the right and negative charges moving to the left both result in current to the right).

Without yet doing any math, we can begin to see why Bob's conclusion could possibly agree with Ann's. With a current to the right and a right-moving point charge, as we noted above, Bob does witness a magnetic force on the point charge toward the wire. But now we see that there is also an electric force due to the net positive charge density on the wire. This will of course repel the positive point charge, so if the magnitude of this repulsive electric force happens to equal the magnitude of the attractive magnetic force, then Bob and Ann will agree, as they must!

Now for the Math

In principle the electric and magnetic forces on the point charge witnessed by Bob can cancel, but for us to actually confirm that special relativity is consistent with E&M, the math has to work out. There are a number of parts to put together here. We'll start with the charge density. We'll call the separation of neighboring charges in Ann's frame \(L\), and adjust the separations in Bob's frame by length contraction:

Figure 3.4.4 – Charge Densities in Both Frames

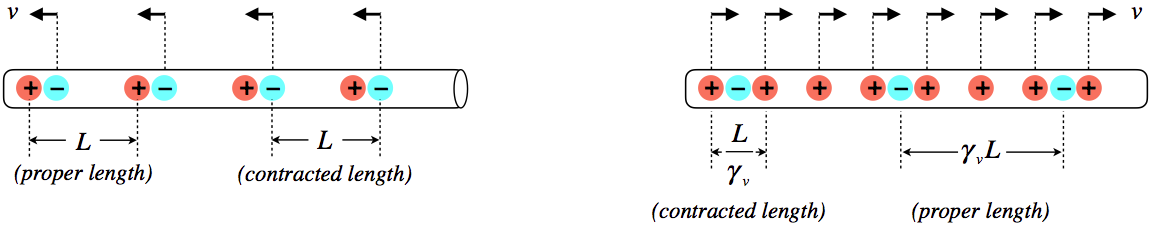
The linear density is the charge per unit length, so:

\[\lambda_{Ann}=\dfrac{+q}{L}+\dfrac{-q}{L}=0\;\;\;\;\;\;\;\;\lambda_{Bob}=\dfrac{+q}{\left(\dfrac{L}{\gamma_v}\right)}+\dfrac{-q}{\gamma_vL}=\gamma_v\dfrac{q}{L}\left(1-\dfrac{1}{\gamma_v^2}\right)=\gamma_v\dfrac{q}{L}\left(\dfrac{v}{c}\right)^2\]

From Physics 9C, we have a formula for the electric field of a line of charge, in terms of its line density. The electric field seen by Ann is clearly zero, and for Bob it is:

\[E_{Bob}=\dfrac{\lambda}{2\pi\epsilon_or}=\left(\dfrac{v^2}{c^2\epsilon_o}\right)\left(\dfrac{\gamma_vq}{2\pi rL}\right)\]

Okay, now we need the magnetic field. We start by reminding ourselves how to get the current from a moving charge density:

\[I=\dfrac{dq}{dt}=\dfrac{dq}{dx}\dfrac{dx}{dt}=\lambda v\]

Note that for Bob, only the positive charges are moving, so the \(\lambda\) that appears in this formula is the charge density of the positive charges only, not the total charge density. So the current is, according to Bob:

\[I=\left(\gamma_v\dfrac{q}{L}\right)v\]

We also have a formula for the magnetic field from the current of a long straight wire from Physics 9C, and plugging this current into it gives the magnetic field seen by Bob:

\[B_{Bob}=\dfrac{\mu_oI}{2\pi r}=\left(\mu_ov\right)\left(\dfrac{\gamma_vq}{2\pi rL}\right)\]

All that remains is to compute the Lorentz force measured by Bob. We have already establish that the electric and magnetic forces are in opposite directions, and since the motion of the point charge is perpendicular to the magnetic field, we have:

\[\vec F = Q\vec E + Q\vec v\times\vec B \;\;\;\Rightarrow\;\;\; F_{Bob}=Q\left(\dfrac{v^2}{c^2\epsilon_o}\right)\left(\dfrac{\gamma_vq}{2\pi rL}\right) - Qv\left(\mu_ov\right)\left(\dfrac{\gamma_vq}{2\pi rL}\right)=\left(\dfrac{1}{c^2\epsilon_o}-\mu_o\right)\left(\dfrac{\gamma_vv^2qQ}{2\pi rL}\right)\]

And now the calculation is completed at last using another result from Physics 9C:

\[c^2=\dfrac{1}{\mu_o\epsilon_o}\;\;\;\Rightarrow\;\;\; F_{Bob}=0\]
 

Full Unification Of Electricity and Magnetism

What this thought experiment shows us is the remarkable unification of the electric and magnetic forces started by Maxwell and completed by Einstein. Maxwell showed that a single source (electric charge) is responsible for both fields and is affected by both fields. With special relativity, Einstein went a step further, and showed that both fields are actually a single field, which has electric and magnetic properties that will be manifested differently depending upon the inertial frame in which they are observed.

It is actually possible to derive specifically how electric and magnetic fields mix into each other as one changes reference frames, in the same way that the Lorentz transformations describe how position and time variables mix into each other. We won't reproduce the derivation here, but here is the final result:

\[\begin{array}{l} \vec {E'}_\parallel = \vec E_\parallel & \vec {B'}_\parallel = \vec B_\parallel \\ \vec {E'}_\perp =\gamma_v\left(\vec E_\perp+\vec v\times\vec B\right) & \vec {B'}_\perp =\gamma_v\left(\vec B_\perp-\dfrac{1}{c^2}\vec v\times\vec E\right) \end{array}\]

In these formulas, the quantities require some explanation. The primed frame is moving with a velocity \(\vec v\) relative to the unprimed frame. The field vectors with no subscripts are the full field vectors, while those with the "\(\parallel\)" subscript are the field components parallel to \(\vec v\), and those with the "\(\perp\)" subscript are the field components perpendicular to \(\vec v\).