5.2: Non-Inertial Frames
- Page ID
- 18408
Linear Accelerated Frames
Let us return for a moment all the way back to Section 1.8, where we discussed relative motion, and in particular, the Galilean transformation equations. If you recall, this discussion was about comparing what one observer sees to what another observer sees, and the model we used simplified things by having the observers in linear relative motion at a constant speed along their common \(x\)-axis, with their clocks synchronized so that \(t'=t=0\) when their origins coincide:
Figure 5.2.1 – Relating Coordinates of Linear Reference Frames
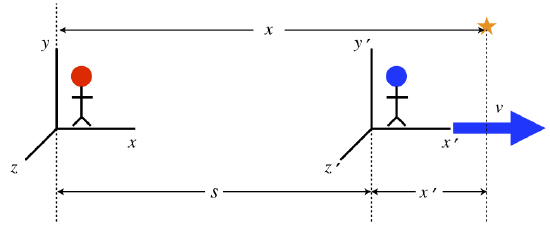
\[\begin{array}{l} t' = t \\ x' = x-vt \\y'=y \\ z'=z \end{array} \]
These equations relate how one observer logs an event in terms of position and time to how the other person logs it. Suppose these two people are observing the motion of an object. Example 1.8.2 in that section shows how we can use the transformation equations to relate the velocities witnessed by the two observers of a common object. Suppose now we want to relate the accelerations witnessed by both. Clearly with \(v\) being a constant, its derivative is zero, which means that both observers agree upon the acceleration, even the component along the \(x\)-direction:
\[\dfrac{dx'}{dt'}=\dfrac{d\left(x-vt\right)}{dt'}=\dfrac{d\left(x-vt\right)}{dt}=\dfrac{dx}{dt}-v\;\;\;\Rightarrow\;\;\; \dfrac{d^2x'}{dt'^2}=\dfrac{d^2x}{dt^2}-\cancelto{0}{\dfrac{dv}{dt}}\]
Suppose, however, that the primed frame is accelerating relative to the unprimed frame. Then the separation of the frames (shown as an \(s\) in the diagram above) has a different time dependence, and we get different transformation equations. We once again simplify things again as much as possible by insisting that:
- the acceleration is a constant value \(a\), along the line of motion in the \(+x\)-direction
- the relative velocities of the frames at the common starting time of \(t'=t=0\) is \(v_o\) in the \(+x\)-direction
- the origins coincide at the common starting time of \(t'=t=0\)
This gives us the following transformation equations:
\[\begin{array}{l} t' = t \\ x' = x-v_ot-\frac{1}{2}at^2 \\y'=y \\ z'=z \end{array} \]
In this case, the two observers would not agree on the acceleration of the commonly-observed object, as it would differ in its \(x\)-component by an amount \(a\):
\[\dfrac{d^2x'}{dt'^2} = \dfrac{d^2x}{dt^2}-\cancelto{0}{\dfrac{dv_o}{dt}}-a\]
Fictitious Forces
Now that we are talking about accelerations, the question of forces comes up. Consider an object that remains at rest in the unprimed frame. That observer must conclude, according to Newton's second law, that it is not experiencing a net force. Naturally this observer can do a careful analysis of all the forces (friction, normal, spring, etc.) that appear on the free-body diagram for that object to confirm that the forces all add up to zero.
What about the other observer's analysis of Newton's second law? The primed observer does not see the object experiencing zero acceleration, as the transformation between their frame and the frame of the other observer demonstrates. This observer therefore concludes that there must be a net force on the object, to accelerate it. But the analysis performed by the unprimed observer who looked at all the physical forces will not come out different for the primed observer – the spring scale used to measure a normal force will not read something different for these two people. So how does this primed observer confirm Newton's second law? They must invent a new, "mystery force" that has no apparent source. We call such a force that comes about purely because the frame in which it is observed is accelerating fictitious. A frame in which there are no fictitious forces present is called an inertial frame, and frames that give rise to fictitious forces are called non-inertial.
One of the defining characteristics of a fictitious force is that it results in the same acceleration regardless of any physical features of the object, because it is the acceleration of the non-inertial frame that is actually witnessed. Given that the same acceleration is observed for all objects of all masses, the accelerated observer would have to conclude that the fictitious force is proportional to the mass of the object.
\[\left. \begin{array}{l} \text{fictitious force }\mathcal F_1\text{ on }m_1\text{ and Newton's 2nd law:} && a = \dfrac{\mathcal F_1}{m_1} \\ \text{fictitious force }\mathcal F_2\text{ on }m_2\text{ and Newton's 2nd law:} && a = \dfrac{\mathcal F_2}{m_2} \end{array} \right\} \;\;\;\Rightarrow\;\;\; \dfrac{\mathcal F_1}{m_1} = \dfrac{\mathcal F_2}{m_2}\]
But wait, there is a force we use all the time that satisfies this very property – gravity! The force of gravity is given by \(mg\), and indeed every object in free fall is seen to accelerate exactly the same amount. So is gravity a fictitious force? We know there is a cause for this force – the earth exerts the force on all objects in proportion to their mass, so maybe gravity just coincidentally resembles a fictitious force. But in fact Einstein, in his theory of general relativity, proposed that gravity is essentially a fictitious force. He posited what he called the equivalence principle, which stated that an observer in a closed room in the absence of gravity that is accelerating in the "upward" direction at a rate of \(9.8\frac{m}{s^2}\) can perform no experiment that will distinguish between that circumstance and the case of the identical closed room on the surface of the earth.
Figure 5.2.2 – Equivalence Principle

As simple as this equivalence might seem to be, it is nevertheless very complicated mathematically to relate a force that attracts objects toward a single point (the center of the planet) to the fictitious force seen in a linearly-accelerated frame, so we unfortunately have to end our discussion of general relativity here and leave it for future coursework in physics.
Rotating Frames
As we know, acceleration that involves speeding up or slowing down in a straight line is not the only variety. We now want to look at how to transform between an inertial frame and one that is rotating around a fixed point in the inertial frame. We will place the origin of the inertial frame on the axis of rotation of the rotating frame, with the axis perpendicular to the plane of rotation coinciding with the \(z\)-axis of the inertial frame. The red axes in the figure below are rotating at a constant rate while the blue axes remain stationary.
Figure 5.2.3 – Relating Coordinates of Rotational Reference Frames
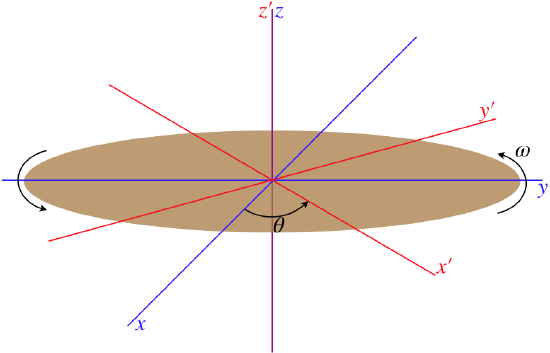
Let's imagine an object at rest on the positive \(x'\)-axis at the moment when all three axes are aligned. The observer at rest in the stationary (unprimed) frame that is watching this object will see it moving in a circle, and at the moment the axes are aligned, it is moving in the \(+y\)-direction. If we call the distance from the \(z\)-axis \(r\), then the speed of the object as seen by the observer in the unprimed frame is \(\omega \;r\). Putting the magnitude and direction together gives us the velocity vector \(\omega \;r\; \widehat j\) for this object, as measured by the stationary observer.
We can write this velocity in terms of the position vector \(\overrightarrow r = r\;\widehat i\) and the rotation vector (which we get from the right-hand rule) \(\overrightarrow \omega = \omega\;\widehat k\) as follows:
\[\omega\;r\; \widehat j = \overrightarrow \omega \times \overrightarrow r\]
This follows very simply, because the cross product of \(\widehat k \times \widehat i\) is just \(\widehat j\).
The nice thing about this way of expressing the velocity is that it doesn't depend upon the specific circumstance of being on the \(x\)-axis. Wherever the object happens to be, as long as it has zero velocity measured in the rotating frame, this cross-product combination of the angular velocity vector and the position vector gives the proper magnitude and direction of the velocity vector seen by the stationary frame.
If an object instead has zero velocity in the stationary frame, then the observer in the primed frame will see the same thing, but in the opposite direction: \(-\overrightarrow \omega \times \overrightarrow r\). Now suppose the object happens to have a non-zero velocity measured in the stationary frame. To get the velocity vector seen in the rotating frame, we simply add vectors according to Equation 1.8.3:
This is the rotational version of the Galilean transformation equations.
Let's suppose we take a snapshot of the position of an object at an instant in time. The observers in the stationary and rotating frames will agree upon the position vector that locates the object. If their axes aren't aligned, then they won't agree upon the components of this vector, but provided their origins still coincide, they will naturally agree that the two position vectors have the same length and point in the same direction. They don't agree upon the velocity of the object, and since the velocity is the time rate of change of the position vector, it must be their time derivatives that are different. Writing the velocities in terms of the time derivatives of position vectors, we get the relationship between the time derivatives:
The "empty" cross-product of "\(\overrightarrow \omega \times\)" is not a typo. The idea is that you just put a vector on the right side of everything in this equation – the derivatives act on the vector, and the vector is the second half of the cross-product. In essence, we have "divided-out" the position vector from the previous equation. This gives us a translation between time derivatives in the two frames - any time derivative of a vector in the rotating frame is equivalent to a time derivative of the vector in the stationary frame minus the cross product of the rotation vector with that same vector.
Alert
Note that this rule only applies to time derivatives, and only when they act on vectors. The former is because snapshots (holding time constant) render the two frames indistinguishable (they only differ in how they evolve through time). The latter is obvious, given that we have to take a cross product with the second term!
Example \(\PageIndex{1}\)
Given that an object can be at rest in one frame and moving in the other, observers in a stationary frame and a rotating frame will not in general agree upon the kinetic energy of an object. Consider a point mass moving directly away from the origin in the rotating frame. Show that the kinetic energy of this object measured in the stationary frame equals the kinetic energy in the rotating frame plus the rotational kinetic energy it gets from rotating along with the rotating frame.
- Solution
-
We compute the kinetic energy using the dot product of the velocity vector with itself, so the kinetic energy in the stationary frame is:
\[ KE_{stationary}=\dfrac{1}{2}mv^2 = \dfrac{1}{2}m\overrightarrow v\cdot\overrightarrow v \nonumber \]
Plugging Equation 5.2.7 into this gives:
\[ \begin{array}{l} KE_{stationary} && = &&\dfrac{1}{2}m\left[\overrightarrow v' + \overrightarrow \omega \times \overrightarrow r\right]\cdot\left[\overrightarrow v' + \overrightarrow \omega \times \overrightarrow r\right] \\ && = && \dfrac{1}{2}m\left[\overrightarrow v'\cdot \overrightarrow v' +2 \overrightarrow v'\cdot\left(\overrightarrow \omega \times \overrightarrow r\right) + \left(\overrightarrow \omega \times \overrightarrow r\right)^2\right]\end{array}\nonumber \]
With the object moving directly radially in the rotating frame, it must be that \(\overrightarrow v'\) is parallel to \(\overrightarrow r\), but the cross product \(\overrightarrow \omega \times \overrightarrow r\) is necessarily perpendicular to \(\overrightarrow r\). This means that the dot product in the middle term is between two perpendicular vectors, which gives zero. The last term is a dot product between two vectors that are the same, so it just gives the magnitude-squared of that vector. The vector \(\overrightarrow r\) is perpendicular to \(\overrightarrow \omega\), so the magnitude of the vector that comes from the cross product is:
\[\left|\overrightarrow\omega \times \overrightarrow r\right| = \omega\;r\;\sin 90^o = \omega\;r \nonumber\]
Putting this in above gives:
\[ KE_{stationary}= \dfrac{1}{2}mv'^2 + \dfrac{1}{2}mr^2\omega^2 \nonumber \]
The point mass has a moment of inertia equal to \(mr^2\) relative to the axis of rotation, so the second term is precisely the rotational energy around that axis, \(\frac{1}{2}I\omega^2\).
More Fictitious Forces
Every point on the rotating frame is accelerating, so if we are observing from that frame, we should expect to witness mysterious accelerations of objects that are not accelerating in the unprimed frame. That is, the primed observer will not be able to pinpoint a true physical force causing it to accelerate, and will need to invent a fictitious force to explain this acceleration with Newton's second law. To determine this force, we first need to derive a translation between accelerations in the two frames. We get the acceleration by taking the derivative of the velocity, so we apply Equation 5.2.8 to the velocity vector in the stationary frame:
\[\left[\dfrac{d}{dt}\overrightarrow v\right]_{stationary} = \left[\dfrac{d}{dt}\overrightarrow v\right]_{rotating} +\overrightarrow \omega \times \overrightarrow v \]
The left side of this equation is the acceleration observed in the stationary frame, but we want it in terms of the acceleration in the rotating frame, so now we plug in Equation 5.2.7:
\[\overrightarrow a = \left[\dfrac{d}{dt}\left(\overrightarrow v' + \overrightarrow \omega \times \overrightarrow r\right)\right]_{rotating} +\overrightarrow \omega \times \left(\overrightarrow v' + \overrightarrow \omega \times \overrightarrow r\right) \]
Now apply the derivative, noting that \(\omega\) is a constant and the derivative of the position vector in the stationary frame is the velocity in that frame:
\[\overrightarrow a = \overrightarrow a' +2 \overrightarrow \omega \times \overrightarrow v' + \overrightarrow \omega \times \left(\overrightarrow \omega \times \overrightarrow r\right)\ \]
Okay, suppose we have a set of real forces (tension, normal, etc.) acting on the object, resulting in a net force, and according to Newton's 2nd law, an acceleration. The net force that the observer measures for this object is therefore simply \(m\overrightarrow a\). But this isn't the net force measured in the rotating frame. This observer sees the object affected by these forces plus two other fictitious forces that arise from the rotation of the frame from which this observer is making measurements. Specifically, the rotating observer measures a net force given by:
\[\overrightarrow F' = \overrightarrow F - 2m\;\overrightarrow\omega \times \overrightarrow v' - m\;\overrightarrow\omega \times \left(\overrightarrow\omega \times\overrightarrow r\right)\]
The first of the two fictitious force terms, which depends upon the velocity measured in the rotating frame, is called the coriolis force. The second, which doesn't require that the object be moving in the rotating frame, is called the centrifugal force.
Alert
It is a common mistake to confuse the terms "centrifugal" and "centripetal." There are several reasons for this, but the main reason is that when first learning physics, students think that it is natural to continue moving in a circle, and feel like there must be a force that "pulls things away from the center" when they turn corners. From the perspective of the frame that is accelerating, this is the fictitious centrifugal force. But then we are taught that the real force that is acting is causing us to change direction, and the acceleration caused by this force is centripetal. The thing to keep in mind is that "centripetal" refers to a specific kind of acceleration, caused by real forces – it is not a type of force at all. On the other hand, "centrifugal" does refer to a force, albeit a fictitious one that arises because the observer is in a rotating frame.
Note that if the object has zero velocity in the rotating frame, then the net force keeping it going in the circle produces an acceleration that is centripetal, which when multiplied by the mass yields a force vector that has the same magnitude as the centrifugal force vector in the rotating frame, and in the opposite direction.
Example \(\PageIndex{2}\)
An object is at rest in a stationary frame.
- Is this object experiencing centripetal acceleration measured in the stationary frame?
- This same object is now observed in a rotating frame with the same origin as the stationary frame, and the object is not positioned at this origin. Does an observer in this rotating frame measure a centrifugal force acting on the object?
- Reconcile the answers to (a) and (b).
- Solution
-
a. Of course not! The object is not moving at all, let alone in a circular fashion.
b. Yes! The frame is rotating, so \(\overrightarrow\omega\) is not zero, and the object is not at the origin, so \(\overrightarrow r\) is not zero. These vectors are at right angles to each other, so the centrifugal force \(\overrightarrow\omega \times \overrightarrow\omega \times \overrightarrow r\) is not zero.
c. How can there be a centrifugal force but no centripetal acceleration? If this is confusing, it displays once again the confusion of these two terms. Let's think about what the observer in the rotating frame sees: They see the object traveling in a circle at a constant speed, in the direction opposite to their frame's rotation. So this observer sees not only a centrifugal force, but also a coriolis force. After working through all the right-hand rules, we find that the centrifugal force acts outward from the axis of rotation (as it always does), and in this particular case, the coriolis force acts inward toward the axis of rotation. Adding these two forces together gives:
\[\overrightarrow F'_{net}= 2m\omega v' \;\text{(inward)} + m\omega^2 r \;\text{(outward)}\nonumber\]
We know how the velocity measured by the rotating observer is related to the distance from the axis and the rotational speed of the frame, since the object is stationary in the rotating frame:
\[v' = r\omega\nonumber\]
Putting this in above, we find that the net force measured in the rotating frame is:
\[\overrightarrow F'_{net}= 2mr\omega^2\;\text{(inward)} + mr\omega^2 \;\text{(outward)} = mr\omega^2\;\text{(inward)} \nonumber\]
This is exactly the net force needed to keep an object moving in a circle at a constant speed, which makes sense, because this is exactly what the rotating observer sees happening. The combination of the centrifugal force and coriolis force yielded a net force in the rotating frame that resulted in centripetal acceleration measured in that frame! How's that for confusing?


