1.E: The Nature of Science and Physics (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
1.1: Physics: An Introduction
1. Models are particularly useful in relativity and quantum mechanics, where conditions are outside those normally encountered by humans. What is a model?
2. How does a model differ from a theory?
3. If two different theories describe experimental observations equally well, can one be said to be more valid than the other (assuming both use accepted rules of logic)?
4. What determines the validity of a theory?
5. Certain criteria must be satisfied if a measurement or observation is to be believed. Will the criteria necessarily be as strict for an expected result as for an unexpected result?
6. Can the validity of a model be limited, or must it be universally valid? How does this compare to the required validity of a theory or a law?
7. Classical physics is a good approximation to modern physics under certain circumstances. What are they?
8. When is it necessary to use relativistic quantum mechanics?
9. Can classical physics be used to accurately describe a satellite moving at a speed of 7500 m/s? Explain why or why not.
1.2: Physical Quantities and Units
10. Identify some advantages of metric units.
1.3: Accuracy, Precision, and Significant Figures
11. What is the relationship between the accuracy and uncertainty of a measurement?
12. Prescriptions for vision correction are given in units called diopters (D). Determine the meaning of that unit. Obtain information (perhaps by calling an optometrist or performing an internet search) on the minimum uncertainty with which corrections in diopters are determined and the accuracy with which corrective lenses can be produced. Discuss the sources of uncertainties in both the prescription and accuracy in the manufacture of lenses.
Problems & Exercises
1.2: Physical Quantities and Units
13.. The speed limit on some interstate highways is roughly 100 km/h. (a) What is this in meters per second? (b) How many miles per hour is this?
Solution:
a. 27.8m/s
b. 62.1mph
14. A car is traveling at a speed of 33m/s
(a) What is its speed in kilometers per hour?
(b) Is it exceeding the 90km/h
15. Show that 1.0m/s=3.6km/h
[Hint: Show the explicit steps involved in converting 1.0m/s=3.6km/h].
Solution
1.0ms=1.0ms×3600s1hr×1km1000m=3.6km/h
16. American football is played on a 100-yd-long field, excluding the end zones. How long is the field in meters? (Assume that 1 meter equals 3.281 feet.)
17. Soccer fields vary in size. A large soccer field is 115 m long and 85 m wide. What are its dimensions in feet and inches? (Assume that 1 meter equals 3.281 feet.)
Solution
length: 377ft;4.53×103in:width:280ft;3.3×103in
18. What is the height in meters of a person who is 6 ft 1.0 in. tall? (Assume that 1 meter equals 39.37 in.)
19. Mount Everest, at 29,028 feet, is the tallest mountain on the Earth. What is its height in kilometers? (Assume that 1 kilometer equals 3,281 feet.)
Solution
8.847 km
20. The speed of sound is measured to be 342 m/s on a certain day. What is this in km/h?
21. Tectonic plates are large segments of the Earth’s crust that move slowly. Suppose that one such plate has an average speed of 4.0 cm/year.
(a) What distance does it move in 1 s at this speed?
(b) What is its speed in kilometers per million years?
Solution
(a) 1.3×10−9m
(b) 40km/My
22. (a) Refer to Table to determine the average distance between the Earth and the Sun. Then calculate the average speed of the Earth in its orbit in kilometers per second.
(b) What is this in meters per second?
1.3: Accuracy, Precision, and Significant Figures
23. Suppose that your bathroom scale reads your mass as 65 kg with a 3% uncertainty. What is the uncertainty in your mass (in kilograms)?
Solution
2 kg
24. A good-quality measuring tape can be off by 0.50 cm over a distance of 20 m. What is its percent uncertainty?
25. (a) A car speedometer has a 5.0 uncertainty. What is the range of possible speeds when it reads 90km/h?
(b) Convert this range to miles per hour. (1km=0.6214mi)
Solution
a. 85.5to 94.5 km/h
b. 53.1to 58.7 mi/h
26. An infant’s pulse rate is measured to be 130±5 beats/min. What is the percent uncertainty in this measurement?
27. (a) Suppose that a person has an average heart rate of 72.0 beats/min. How many beats does he or she have in 2.0 y?
(b) In 2.00 y?
(c) In 2.000 y?
Solution
(a) 7.6×107 beats
(b) 7.57×107 beats
(c) 7.57×107 beats
28. A can contains 375 mL of soda. How much is left after 308 mL is removed?
29. State how many significant figures are proper in the results of the following calculations:
(a) (106.7)(98.2)/(46.210)(1.01)
(b) (18.7)2
(c) (1.60×10−19)(3712)
Solution
a. 3
b. 3
c.3
30. (a) How many significant figures are in the numbers 99 and 100?
(b) If the uncertainty in each number is 1, what is the percent uncertainty in each?
(c) Which is a more meaningful way to express the accuracy of these two numbers, significant figures or percent uncertainties?
31. (a) If your speedometer has an uncertainty of 2.0km/h at a speed of 90km/h. what is the percent uncertainty?
(b) If it has the same percent uncertainty when it reads 60km/h, what is the range of speeds you could be going?
Solution
(a) 2.2
(b) 59 to 61 km/h
32. (a) A person’s blood pressure is measured to be 120±2 mm Hg. What is its percent uncertainty?
(b) Assuming the same percent uncertainty, what is the uncertainty in a blood pressure measurement of 80 mm Hg?
33. A person measures his or her heart rate by counting the number of beats in 30s. If 40±1 beats are counted in 30.0±0.5s , what is the heart rate and its uncertainty in beats per minute?
Solution
80±3 beats/min
34. What is the area of a circle 3.102cmin diameter?
35. If a marathon runner averages 9.5 mi/h, how long does it take him or her to run a 26.22-mi marathon?
Solution
2.8h
36. A marathon runner completes a 42.188−km course in 2h, 30 min, and 12s. There is an uncertainty of 25m in the distance traveled and an uncertainty of 1 s in the elapsed time.
(a) Calculate the percent uncertainty in the distance.
(b) Calculate the uncertainty in the elapsed time.
(c) What is the average speed in meters per second?
(d) What is the uncertainty in the average speed?
37. The sides of a small rectangular box are measured to be 1.80±0.01cm,2.05±0.02cm, and 3.1±0.1cm long. Calculate its volume and uncertainty in cubic centimeters.
Solution
11±1cm3
38. When non-metric units were used in the United Kingdom, a unit of mass called the pound-mass (lbm) was employed, where 1lbm=0.4539kg
(a) If there is an uncertainty of 0.0001kg in the pound-mass unit, what is its percent uncertainty?
(b) Based on that percent uncertainty, what mass in pound-mass has an uncertainty of 1 kg when converted to kilograms?
39. The length and width of a rectangular room are measured to be 3.955±0.005m and 3.050±0.005m. Calculate the area of the room and its uncertainty in square meters.
Solution
12.06±0.04m2
40. A car engine moves a piston with a circular cross section of 7.500±0.002cm diameter a distance of 3.250±0.001cm to compress the gas in the cylinder.
(a) By what amount is the gas decreased in volume in cubic centimeters?
(b) Find the uncertainty in this volume.
1.4: Approximation
41. How many heartbeats are there in a lifetime?
Solution
Sample answer: 2×109 heartbeats
42. A generation is about one-third of a lifetime. Approximately how many generations have passed since the year 0 AD?
43. How many times longer than the mean life of an extremely unstable atomic nucleus is the lifetime of a human? (Hint: The lifetime of an unstable atomic nucleus is on the order of 10−22s.)
Solution
Sample answer: 2×1031 if an average human lifetime is taken to be about 70 years.
44. Calculate the approximate number of atoms in a bacterium. Assume that the average mass of an atom in the bacterium is ten times the mass of a hydrogen atom. (Hint: The mass of a hydrogen atom is on the order of 10−27kg and the mass of a bacterium is on the order of 10−15kg.)
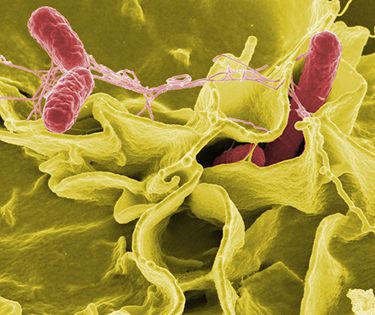
This color-enhanced photo shows Salmonella typhimurium (red) attacking human cells. These bacteria are commonly known for causing foodborne illness. Can you estimate the number of atoms in each bacterium? (credit: Rocky Mountain Laboratories, NIAID, NIH)
45. Approximately how many atoms thick is a cell membrane, assuming all atoms there average about twice the size of a hydrogen atom?
Solution
Sample answer: 50 atoms
46. (a) What fraction of Earth’s diameter is the greatest ocean depth?
(b) The greatest mountain height?
47. (a) Calculate the number of cells in a hummingbird assuming the mass of an average cell is ten times the mass of a bacterium.
(b) Making the same assumption, how many cells are there in a human?
Solution
Sample answers:
(a) 1012 cells/hummingbird
(b) 1016 cells/human
48. Assuming one nerve impulse must end before another can begin, what is the maximum firing rate of a nerve in impulses per second?
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

