25: Geometric Optics (Exercises)
- Page ID
- 4209
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conceptual Questions
25.2: The Law of Reflection
1. Using the law of reflection, explain how powder takes the shine off of a person’s nose. What is the name of the optical effect?
25.3: The Law of Refraction
2. Diffusion by reflection from a rough surface is described in this chapter. Light can also be diffused by refraction. Describe how this occurs in a specific situation, such as light interacting with crushed ice.
3. Why is the index of refraction always greater than or equal to 1?
4. Does the fact that the light flash from lightning reaches you before its sound prove that the speed of light is extremely large or simply that it is greater than the speed of sound? Discuss how you could use this effect to get an estimate of the speed of light.
5. Will light change direction toward or away from the perpendicular when it goes from air to water? Water to glass? Glass to air?
6. Explain why an object in water always appears to be at a depth shallower than it actually is? Why do people sometimes sustain neck and spinal injuries when diving into unfamiliar ponds or waters?
7. Explain why a person’s legs appear very short when wading in a pool. Justify your explanation with a ray diagram showing the path of rays from the feet to the eye of an observer who is out of the water.
8. Why is the front surface of a thermometer curved as shown?
The curved surface of the thermometer serves a purpose.
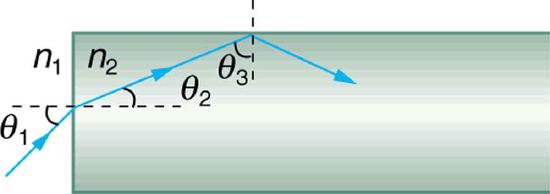
9. Suppose light were incident from air onto a material that had a negative index of refraction, say \(\displaystyle -1.3\); where does the refracted light ray go?
25.4: Total Internal Reflection
10. A ring with a colorless gemstone is dropped into water. The gemstone becomes invisible when submerged. Can it be a diamond? Explain.
11. A high-quality diamond may be quite clear and colorless, transmitting all visible wavelengths with little absorption. Explain how it can sparkle with flashes of brilliant color when illuminated by white light.
12. Is it possible that total internal reflection plays a role in rainbows? Explain in terms of indices of refraction and angles, perhaps referring to the figure. Some of us have seen the formation of a double rainbow. Is it physically possible to observe a triple rainbow?

Double rainbows are not a very common observance. (credit: InvictusOU812, Flickr)
13. The most common type of mirage is an illusion that light from faraway objects is reflected by a pool of water that is not really there. Mirages are generally observed in deserts, when there is a hot layer of air near the ground. Given that the refractive index of air is lower for air at higher temperatures, explain how mirages can be formed.
25.6: Image Formation by Lenses
14. It can be argued that a flat piece of glass, such as in a window, is like a lens with an infinite focal length. If so, where does it form an image? That is, how are \(\displaystyle d_{i}\) and \(\displaystyle d_{o}\) related?
15. You can often see a reflection when looking at a sheet of glass, particularly if it is darker on the other side. Explain why you can often see a double image in such circumstances.
16. When you focus a camera, you adjust the distance of the lens from the film. If the camera lens acts like a thin lens, why can it not be a fixed distance from the film for both near and distant objects?
17. A thin lens has two focal points, one on either side, at equal distances from its center, and should behave the same for light entering from either side. Look through your eyeglasses (or those of a friend) backward and forward and comment on whether they are thin lenses.
18. Will the focal length of a lens change when it is submerged in water? Explain.
25.7: Image Formation by Mirrors
19. What are the differences between real and virtual images? How can you tell (by looking) whether an image formed by a single lens or mirror is real or virtual?
20. Can you see a virtual image? Can you photograph one? Can one be projected onto a screen with additional lenses or mirrors? Explain your responses.
21. Is it necessary to project a real image onto a screen for it to exist?
22. At what distance is an image always located--at \(\displaystyle d_{o}\), \(\displaystyle d_{i}\), or \(\displaystyle f\)?
23. Under what circumstances will an image be located at the focal point of a lens or mirror?
24. What is meant by a negative magnification? What is meant by a magnification that is less than 1 in magnitude?
25. Can a case 1 image be larger than the object even though its magnification is always negative? Explain.
26. The figure shows a light bulb between two mirrors. One mirror produces a beam of light with parallel rays; the other keeps light from escaping without being put into the beam. Where is the filament of the light in relation to the focal point or radius of curvature of each mirror?
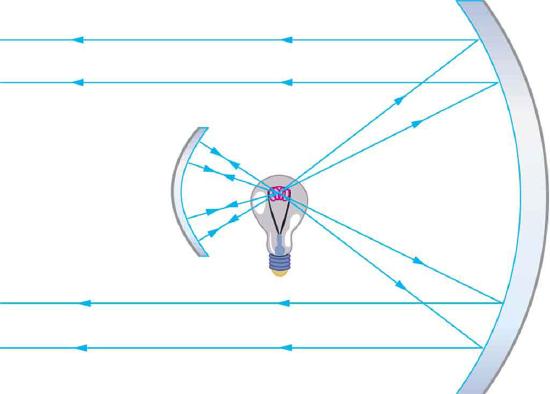
The two mirrors trap most of the bulb’s light and form a directional beam as in a headlight.
27. Devise an arrangement of mirrors allowing you to see the back of your head. What is the minimum number of mirrors needed for this task?
28. If you wish to see your entire body in a flat mirror (from head to toe), how tall should the mirror be? Does its size depend upon your distance away from the mirror? Provide a sketch.
29. It can be argued that a flat mirror has an infinite focal length. If so, where does it form an image? That is, how are \(\displaystyle d_{i}\) and \(\displaystyle d_{o}\) related?
30. Why are diverging mirrors often used for rear-view mirrors in vehicles? What is the main disadvantage of using such a mirror compared with a flat one?
Problems & Exercises
25.1: The Ray Aspect of Light
31. Suppose a man stands in front of a mirror as shown in the figure. His eyes are 1.65 m above the floor, and the top of his head is 0.13 m higher. Find the height above the floor of the top and bottom of the smallest mirror in which he can see both the top of his head and his feet. How is this distance related to the man’s height?
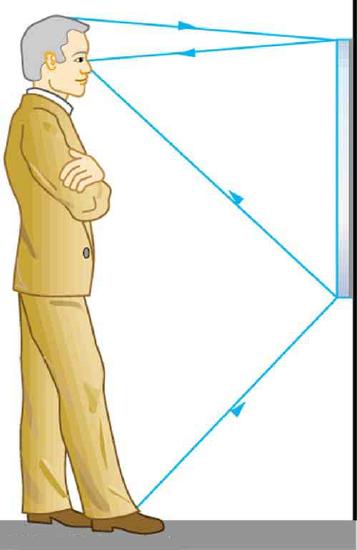
A full-length mirror is one in which you can see all of yourself. It need not be as big as you, and its size is independent of your distance from it.
Solution
top \(\displaystyle 1.715 m\) from floor; bottom \(\displaystyle 0.825 m\) from floor; height = \(\displaystyle 0.890 m\), or precisely one-half the height of the person.
25.2: The Law of Reflection
32. Show that when light reflects from two mirrors that meet each other at a right angle, the outgoing ray is parallel to the incoming ray, as illustrated in the following figure.
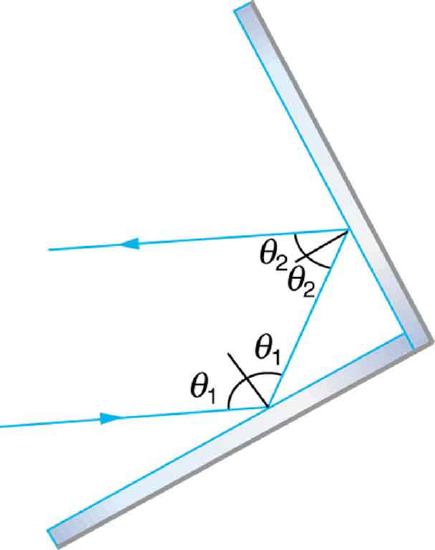
A corner reflector sends the reflected ray back in a direction parallel to the incident ray, independent of incoming direction.
33. Light shows staged with lasers use moving mirrors to swing beams and create colorful effects. Show that a light ray reflected from a mirror changes direction by \(\displaystyle 2\theta\) when the mirror is rotated by an angle \(\displaystyle \theta\).
34. A flat mirror is neither converging nor diverging. To prove this, consider two rays originating from the same point and diverging at an angle \(\displaystyle \theta\). Show that after striking a plane mirror, the angle between their directions remains \(\displaystyle \theta\).
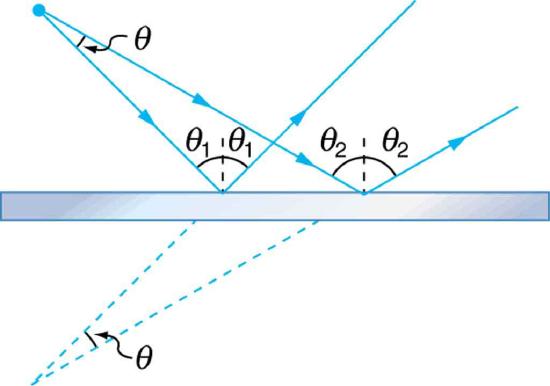
A flat mirror neither converges nor diverges light rays. Two rays continue to diverge at the same angle after reflection.
25.3: The Law of Refraction
35.What is the speed of light in water? In glycerine?
Solution
water --> \(\displaystyle 2.25 \times 10^{8} m/s\)
glycerine --> \(\displaystyle 2.04 \times 10^{8} m/s\)
36. What is the speed of light in air? In crown glass?
37. Calculate the index of refraction for a medium in which the speed of light is \(\displaystyle 2.012 \times 10^{8} m/s\), and identify the most likely substance based on the table.
Solution
\(\displaystyle 1.490\), polystyrene
38. In what substance in the table is the speed of light \(\displaystyle 2.290 \times 10^{8} m/s\)?
39. There was a major collision of an asteroid with the Moon in medieval times. It was described by monks at Canterbury Cathedral in England as a red glow on and around the Moon. How long after the asteroid hit the Moon, which is \(\displaystyle 3.84 \times 10^{5} km\) away, would the light first arrive on Earth?
Solution
\(\displaystyle 1.28 s\)
40. A scuba diver training in a pool looks at his instructor as shown in the figure. What angle does the ray from the instructor’s face make with the perpendicular to the water at the point where the ray enters? The angle between the ray in the water and the perpendicular to the water is \(\displaystyle 25.0^{\circ}\).
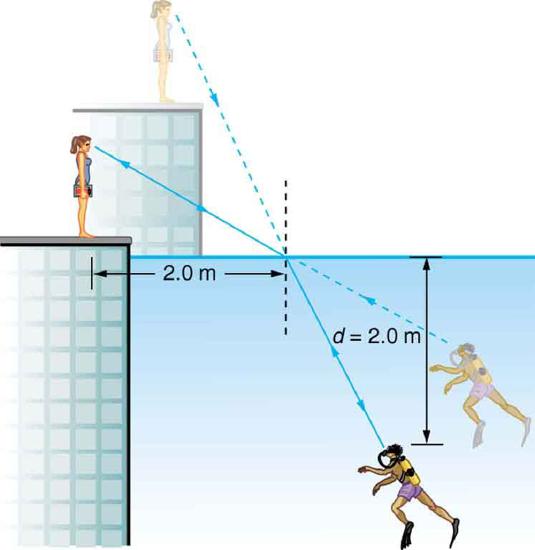
A scuba diver in a pool and his trainer look at each other.
41. Components of some computers communicate with each other through optical fibers having an index of refraction \(\displaystyle n=1.55\). What time in nanoseconds is required for a signal to travel 0.200 m through such a fiber?
Solution
\(\displaystyle 1.03 ns\)
42. Using information in the above figure,
(a) Given that the angle between the ray in the water and the perpendicular to the water is \(\displaystyle 25.0^{\circ}\), find the height of the instructor’s head above the water, noting that you will first have to calculate the angle of refraction.
(b) find the apparent depth of the diver’s head below water as seen by the instructor. Assume the diver and the diver's image are the same horizontal distance from the normal.
43. Suppose you have an unknown clear substance immersed in water, and you wish to identify it by finding its index of refraction. You arrange to have a beam of light enter it at an angle of \(\displaystyle 45.0^{\circ}\), and you observe the angle of refraction to be \(\displaystyle 40.3^{\circ}\). What is the index of refraction of the substance and its likely identity?
Solution
\(\displaystyle n = 1.46\), fused quartz
44. On the Moon’s surface, lunar astronauts placed a corner reflector, off which a laser beam is periodically reflected. The distance to the Moon is calculated from the round-trip time. What percent correction is needed to account for the delay in time due to the slowing of light in Earth’s atmosphere? Assume the distance to the Moon is precisely \(\displaystyle 3.84 \times 10^{8} m\) and Earth’s atmosphere (which varies in density with altitude) is equivalent to a layer 30.0 km thick with a constant index of refraction \(\displaystyle n = 1.000293\).
45. Suppose Figure 6 represents a ray of light going from air through crown glass into water, such as going into a fish tank. Calculate the amount the ray is displaced by the glass (\(\displaystyle \Delta x\)), given that the incident angle is \(\displaystyle 40.0^{\circ}\) and the glass is 1.00 cm thick.
46. The figure shows a ray of light passing from one medium into a second and then a third. Show that \(\displaystyle \theta_{3}\) is the same as it would be if the second medium were not present (provided total internal reflection does not occur).
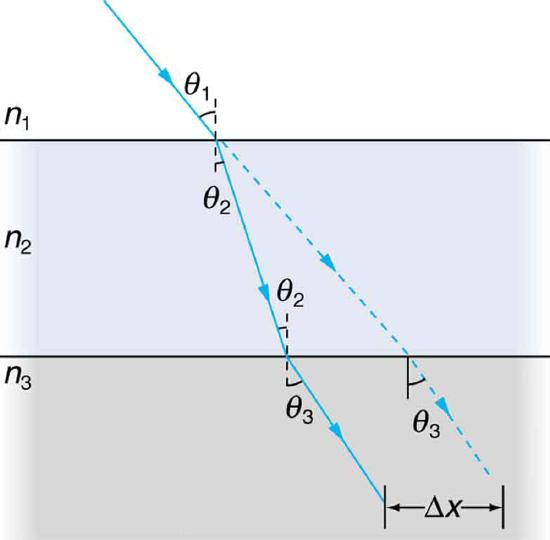
A ray of light passes from one medium to a third by traveling through a second. The final direction is the same as if the second medium were not present, but the ray is displaced by \(\displaystyle \Delta x\) (shown exaggerated).
47. Unreasonable Results
Suppose light travels from water to another substance, with an angle of incidence of \(\displaystyle 10.0^{\circ}\) and an angle of refraction of \(\displaystyle 14.9^{\circ}\).
(a) What is the index of refraction of the other substance?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
Solution
(a) 0.898
(b) can't have \(\displaystyle n \lt 1.00\) since this would imply a speed greater than \(\displaystyle c\)
(c) Refracted angle is too big relative to the angle of incidence.
48. Construct Your Own Problem
Consider sunlight entering the Earth’s atmosphere at sunrise and sunset -- that is, at a \(\displaystyle 90^{\circ}\) incident angle. Taking the boundary between nearly empty space and the atmosphere to be sudden, calculate the angle of refraction for sunlight. This lengthens the time the Sun appears to be above the horizon, both at sunrise and sunset. Now construct a problem in which you determine the angle of refraction for different models of the atmosphere, such as various layers of varying density. Your instructor may wish to guide you on the level of complexity to consider and on how the index of refraction varies with air density.
49. Unreasonable Results
Light traveling from water to a gemstone strikes the surface at an angle of \(\displaystyle 80.0^{\circ}\) and has an angle of refraction of \(\displaystyle 15.2^{\circ}\).
(a) What is the speed of light in the gemstone?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
Solution
(a) \(\displaystyle \frac{c}{5.00}\)
(b) speed of light too slow, since index is much greater than that of diamond
(c) angle of refraction is unreasonable relative to the angle of incidence
25.4: Total Internal Reflection
50. Verify that the critical angle for light going from water to air is \(\displaystyle 48.6^{\circ}\), as discussed at the end of the in-chapter example, regarding the critical angle for light traveling in a polystyrene (a type of plastic) pipe surrounded by air.
51. (a) At the end of the example, it was stated that the critical angle for light going from diamond to air is \(\displaystyle 24.4^{\circ}\). Verify this.
(b) What is the critical angle for light going from zircon to air?
52. An optical fiber uses flint glass clad with crown glass. What is the critical angle?
Solution
\(\displaystyle 66.3^{\circ}\)
53. At what minimum angle will you get total internal reflection of light traveling in water and reflected from ice?
54. Suppose you are using total internal reflection to make an efficient corner reflector. If there is air outside and the incident angle is \(\displaystyle 45.0^{\circ}\) what must be the minimum index of refraction of the material from which the reflector is made?
Solution
\(\displaystyle \gt 1.414\)
55. You can determine the index of refraction of a substance by determining its critical angle.
(a) What is the index of refraction of a substance that has a critical angle of \(\displaystyle 68.4^{\circ}\) when submerged in water? What is the substance, based on this link.
(b) What would the critical angle be for this substance in air?
56. A ray of light, emitted beneath the surface of an unknown liquid with air above it, undergoes total internal reflection as shown in the figure. What is the index of refraction for the liquid and its likely identification?
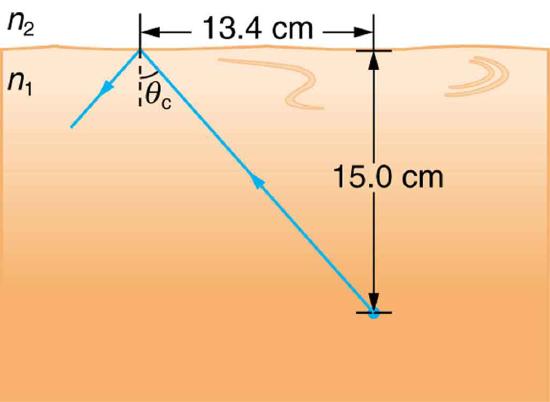
A light ray inside a liquid strikes the surface at the critical angle and undergoes total internal reflection.
Solution
1.50; benzene
57. A light ray entering an optical fiber surrounded by air is first refracted and then reflected as shown in the figure. Show that if the fiber is made from crown glass, any incident ray will be totally internally reflected.
A light ray enters the end of a fiber, the surface of which is perpendicular to its sides. Examine the conditions under which it may be totally internally reflected.
25.5: Dispersion: The Rainbow and Prisms
58. (a) What is the ratio of the speed of red light to violet light in diamond, based on the table?
(b) What is this ratio in polystyrene?
(c) Which is more dispersive?
59. A beam of white light goes from air into water at an incident angle of \(\displaystyle 75.0^{\circ}\). At what angles are the red (660 nm) and violet (410 nm) parts of the light refracted?
Solution
\(\displaystyle 46.5^{\circ}, red; 46.0^{\circ}, violet\)
60. By how much do the critical angles for red (660 nm) and violet (410 nm) light differ in a diamond surrounded by air?
61. (a) A narrow beam of light containing yellow (580 nm) and green (550 nm) wavelengths goes from polystyrene to air, striking the surface at a \(\displaystyle 30.0^{\circ}\) incident angle. What is the angle between the colors when they emerge?
(b) How far would they have to travel to be separated by 1.00 mm?
Solution
(a) \(\displaystyle 0.043^{\circ}\)
(b) \(\displaystyle 1.33 m\)
62. A parallel beam of light containing orange (610 nm) and violet (410 nm) wavelengths goes from fused quartz to water, striking the surface between them at a \(\displaystyle 60.0^{\circ}\) incident angle. What is the angle between the two colors in water?
63. A ray of 610 nm light goes from air into fused quartz at an incident angle of \(\displaystyle 55.0^{\circ}\) At what incident angle must 470 nm light enter flint glass to have the same angle of refraction?
Solution
\(\displaystyle 71.3^{\circ}\)
64. A narrow beam of light containing red (660 nm) and blue (470 nm) wavelengths travels from air through a 1.00 cm thick flat piece of crown glass and back to air again. The beam strikes at a \(\displaystyle 30.0^{\circ}\) incident angle.
(a) At what angles do the two colors emerge?
(b) By what distance are the red and blue separated when they emerge?
65. A narrow beam of white light enters a prism made of crown glass at a \(\displaystyle 45.0^{\circ}\) incident angle, as shown in the figure. At what angles, \(\displaystyle \theta_{R}\) and \(\displaystyle \theta_{V}\), do the red (660 nm) and violet (410 nm) components of the light emerge from the prism?
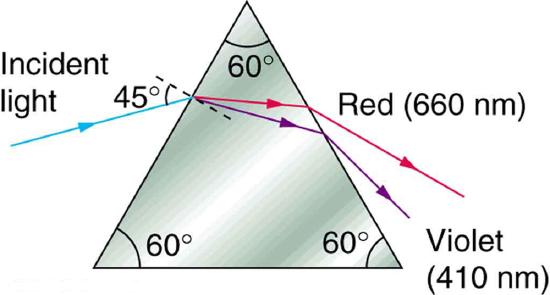
This prism will disperse the white light into a rainbow of colors. The incident angle is \(\displaystyle 45.0^{\circ}\), and the angles at which the red and violet light emerge are \(\displaystyle \theta_{R}\) and \(\displaystyle \theta_{V}\).
Solution
\(\displaystyle 53.5^{\circ}, red; 55.2^{\circ}, violet\)
25.6: Image Formation by Lenses
66. What is the power in diopters of a camera lens that has a 50.0 mm focal length?
67. Your camera’s zoom lens has an adjustable focal length ranging from 80.0 to 200 mm. What is its range of powers?
Solution
\(\displaystyle 5.00 to 12.5 D\)
68. What is the focal length of 1.75 D reading glasses found on the rack in a pharmacy?
69. You note that your prescription for new eyeglasses is –4.50 D. What will their focal length be?
Solution
\(\displaystyle -0.222 m\)
70. How far from the lens must the film in a camera be, if the lens has a 35.0 mm focal length and is being used to photograph a flower 75.0 cm away? Explicitly show how you follow the steps in the Problem-Solving Strategy for lenses.
71. A certain slide projector has a 100 mm focal length lens.
(a) How far away is the screen, if a slide is placed 103 mm from the lens and produces a sharp image?
(b) If the slide is 24.0 by 36.0 mm, what are the dimensions of the image? Explicitly show how you follow the steps in the Problem-Solving Strategy for lenses.
Solution
(a) 3.43 m
(b) 0.800 by 1.20 m
72. A doctor examines a mole with a 15.0 cm focal length magnifying glass held 13.5 cm from the mole
(a) Where is the image?
(b) What is its magnification?
(c) How big is the image of a 5.00 mm diameter mole?
Solution
(a) \(\displaystyle -1.35 m\) (on the object side of the lens)
(b) +10.0
(c) 5.00 cm
73. How far from a piece of paper must you hold your father’s 2.25 D reading glasses to try to burn a hole in the paper with sunlight?
Solution
44.4 cm
74. A camera with a 50.0 mm focal length lens is being used to photograph a person standing 3.00 m away.
(a) How far from the lens must the film be?
(b) If the film is 36.0 mm high, what fraction of a 1.75 m tall person will fit on it?
(c) Discuss how reasonable this seems, based on your experience in taking or posing for photographs.
75. A camera lens used for taking close-up photographs has a focal length of 22.0 mm. The farthest it can be placed from the film is 33.0 mm.
(a) What is the closest object that can be photographed?
(b) What is the magnification of this closest object?
Solution
(a) 6.60 cm
(b) -0.333
76. Suppose your 50.0 mm focal length camera lens is 51.0 mm away from the film in the camera.
(a) How far away is an object that is in focus?
(b) What is the height of the object if its image is 2.00 cm high?
77. (a) What is the focal length of a magnifying glass that produces a magnification of 3.00 when held 5.00 cm from an object, such as a rare coin?
(b) Calculate the power of the magnifier in diopters.
(c) Discuss how this power compares to those for store-bought reading glasses (typically 1.0 to 4.0 D). Is the magnifier’s power greater, and should it be?
Solution
(a) +7.50 cm
(b) 13.3 D
(c) much greater
78. What magnification will be produced by a lens of power –4.00 D (such as might be used to correct myopia) if an object is held 25.0 cm away?
79. In the "Image Produced by a Magnifying Glass" example, the magnification of a book held 7.50 cm from a 10.0 cm focal length lens was found to be 4.00.
(a) Find the magnification for the book when it is held 8.50 cm from the magnifier.
(b) Do the same for when it is held 9.50 cm from the magnifier.
(c) Comment on the trend in m as the object distance increases as in these two calculations.
Solution
(a) +6.67
(b) +20.0
(c) The magnification increases without limit (to infinity) as the object distance increases to the limit of the focal distance.
80. Suppose a 200 mm focal length telephoto lens is being used to photograph mountains 10.0 km away. (a) Where is the image? (b) What is the height of the image of a 1000 m high cliff on one of the mountains?
81. A camera with a 100 mm focal length lens is used to photograph the sun and moon. What is the height of the image of the sun on the film, given the sun is \(\displaystyle 1.40 \times 10^{6} km\) in diameter and is \(\displaystyle 1.50 \times 10^{8} km\) away?
Solution
-0933 mm
82. Combine thin lens equations to show that the magnification for a thin lens is determined by its focal length and the object distance and is given by \(\displaystyle m = f/\left(f - d_{o}\right)\).
25.7: Image Formation by Mirrors
83. What is the focal length of a makeup mirror that has a power of 1.50 D?
Solution
+0.667 m
84. Some telephoto cameras use a mirror rather than a lens. What radius of curvature mirror is needed to replace a 800 mm focal length telephoto lens?
85. (a) Calculate the focal length of the mirror formed by the shiny back of a spoon that has a 3.00 cm radius of curvature.
(b) What is its power in diopters?
Solution
(a) \(\displaystyle -1.5 \times 10^{-2} m\)
(b) \(\displaystyle -66.7 D\)
86. Find the magnification of the heater element in the Concave Reflector example. Note that its large magnitude helps spread out the reflected energy.
87. What is the focal length of a makeup mirror that produces a magnification of 1.50 when a person’s face is 12.0 cm away? Explicitly show how you follow the steps in the "Problem-Solving Strategy for Mirrors."
Solution
+0.360 m (concave)
88. A shopper standing 3.00 m from a convex security mirror sees his image with a magnification of 0.250. (a) Where is his image? (b) What is the focal length of the mirror? (c) What is its radius of curvature? Explicitly show how you follow the steps in the "Problem-Solving Strategy for Mirrors."
89. An object 1.50 cm high is held 3.00 cm from a person’s cornea, and its reflected image is measured to be 0.167 cm high.
(a) What is the magnification?
(b) Where is the image?
(c) Find the radius of curvature of the convex mirror formed by the cornea. (Note that this technique is used by optometrists to measure the curvature of the cornea for contact lens fitting. The instrument used is called a keratometer, or curve measurer.)
Solution
(a) +0.111
(b) -0.334 cm (behind "mirror")
(c) 0.752 cm
90. Ray tracing for a flat mirror shows that the image is located a distance behind the mirror equal to the distance of the object from the mirror. This is stated \(\displaystyle d_{i} = -d_{o}\), since this is a negative image distance (it is a virtual image).
(a) What is the focal length of a flat mirror?
(b) What is its power?
91. Show that for a flat mirror \(\displaystyle h_{i} = h_{o}\), knowing that the image is a distance behind the mirror equal in magnitude to the distance of the object from the mirror.
Solution
\[m = \frac{h_{i}}{h_{o}} = - \frac{d_{i}}{d_{o}} = - \frac{-d_{o}}{d_{o}} = \frac{d_{o}}{d_{o}} = 1 \rightarrow h_{i} = h_{o}\]
92. Use the law of reflection to prove that the focal length of a mirror is half its radius of curvature. That is, prove that \(\displaystyle f = R/2\). Note this is true for a spherical mirror only if its diameter is small compared with its radius of curvature.
93. Referring to the electric room heater considered in the first example in this section, calculate the intensity of IR radiation in \(\displaystyle W/m^{2}\) projected by the concave mirror on a person 3.00 m away. Assume that the heating element radiates 1500 W and has an area of \(\displaystyle 100 cm^{2}\), and that half of the radiated power is reflected and focused by the mirror.
Solution
\(\displaystyle 6.82 kW/m^{2}\)
94. Consider a 250-W heat lamp fixed to the ceiling in a bathroom. If the filament in one light burns out then the remaining three still work. Construct a problem in which you determine the resistance of each filament in order to obtain a certain intensity projected on the bathroom floor. The ceiling is 3.0 m high. The problem will need to involve concave mirrors behind the filaments. Your instructor may wish to guide you on the level of complexity to consider in the electrical components.
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

