27: Wave Optics (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
27.1: The Wave Aspect of Light: Interference
1. What type of experimental evidence indicates that light is a wave?
2. Give an example of a wave characteristic of light that is easily observed outside the laboratory.
27.2: Huygens's Principle: Diffraction
3. How do wave effects depend on the size of the object with which the wave interacts? For example, why does sound bend around the corner of a building while light does not?
4. Under what conditions can light be modeled like a ray? Like a wave?
5. Go outside in the sunlight and observe your shadow. It has fuzzy edges even if you do not. Is this a diffraction effect? Explain.
6. Why does the wavelength of light decrease when it passes from vacuum into a medium? State which attributes change and which stay the same and, thus, require the wavelength to decrease.
7. Does Huygens’s principle apply to all types of waves?
27.3: Young’s Double Slit Experiment
8. Young’s double slit experiment breaks a single light beam into two sources. Would the same pattern be obtained for two independent sources of light, such as the headlights of a distant car? Explain.
9. Suppose you use the same double slit to perform Young’s double slit experiment in air and then repeat the experiment in water. Do the angles to the same parts of the interference pattern get larger or smaller? Does the color of the light change? Explain.
10. Is it possible to create a situation in which there is only destructive interference? Explain.
11. The figrue shows the central part of the interference pattern for a pure wavelength of red light projected onto a double slit. The pattern is actually a combination of single slit and double slit interference. Note that the bright spots are evenly spaced. Is this a double slit or single slit characteristic? Note that some of the bright spots are dim on either side of the center. Is this a single slit or double slit characteristic? Which is smaller, the slit width or the separation between slits? Explain your responses.

This double slit interference pattern also shows signs of single slit interference. (credit: PASCO)
27.4: Multiple Slit Diffraction
12. What is the advantage of a diffraction grating over a double slit in dispersing light into a spectrum?
13. What are the advantages of a diffraction grating over a prism in dispersing light for spectral analysis?
14. Can the lines in a diffraction grating be too close together to be useful as a spectroscopic tool for visible light? If so, what type of EM radiation would the grating be suitable for? Explain.
15. If a beam of white light passes through a diffraction grating with vertical lines, the light is dispersed into rainbow colors on the right and left. If a glass prism disperses white light to the right into a rainbow, how does the sequence of colors compare with that produced on the right by a diffraction grating?
16. Suppose pure-wavelength light falls on a diffraction grating. What happens to the interference pattern if the same light falls on a grating that has more lines per centimeter? What happens to the interference pattern if a longer-wavelength light falls on the same grating? Explain how these two effects are consistent in terms of the relationship of wavelength to the distance between slits.
17. Suppose a feather appears green but has no green pigment. Explain in terms of diffraction.
18. Suppose a feather appears green but has no green pigment. Explain in terms of diffraction.
27.5: Single Slit Diffraction
19. As the width of the slit producing a single-slit diffraction pattern is reduced, how will the diffraction pattern produced change?
27.6: Limits of Resolution: The Rayleigh Criterion
20. A beam of light always spreads out. Why can a beam not be created with parallel rays to prevent spreading? Why can lenses, mirrors, or apertures not be used to correct the spreading?
27.7: Thin Film Interference
21. What effect does increasing the wedge angle have on the spacing of interference fringes? If the wedge angle is too large, fringes are not observed. Why?
22. How is the difference in paths taken by two originally in-phase light waves related to whether they interfere constructively or destructively? How can this be affected by reflection? By refraction?
23. Is there a phase change in the light reflected from either surface of a contact lens floating on a person’s tear layer? The index of refraction of the lens is about 1.5, and its top surface is dry.
24. In placing a sample on a microscope slide, a glass cover is placed over a water drop on the glass slide. Light incident from above can reflect from the top and bottom of the glass cover and from the glass slide below the water drop. At which surfaces will there be a phase change in the reflected light?
25. Answer the above question if the fluid between the two pieces of crown glass is carbon disulfide.
26. While contemplating the food value of a slice of ham, you notice a rainbow of color reflected from its moist surface. Explain its origin.
27. An inventor notices that a soap bubble is dark at its thinnest and realizes that destructive interference is taking place for all wavelengths. How could she use this knowledge to make a non-reflective coating for lenses that is effective at all wavelengths? That is, what limits would there be on the index of refraction and thickness of the coating? How might this be impractical?
28. A non-reflective coating like the one described in Example works ideally for a single wavelength and for perpendicular incidence. What happens for other wavelengths and other incident directions? Be specific.
29. Why is it much more difficult to see interference fringes for light reflected from a thick piece of glass than from a thin film? Would it be easier if monochromatic light were used?
27.8: Polarization
30. Under what circumstances is the phase of light changed by reflection? Is the phase related to polarization?
31. Can a sound wave in air be polarized? Explain.
32. No light passes through two perfect polarizing filters with perpendicular axes. However, if a third polarizing filter is placed between the original two, some light can pass. Why is this? Under what circumstances does most of the light pass?
33. Explain what happens to the energy carried by light that it is dimmed by passing it through two crossed polarizing filters.
34. When particles scattering light are much smaller than its wavelength, the amount of scattering is proportional to 1/λ4. Does this mean there is more scattering for small λ than large λ? How does this relate to the fact that the sky is blue?
35. Using the information given in the preceding question, explain why sunsets are red.
36. When light is reflected at Brewster’s angle from a smooth surface, it is 100 polarized parallel to the surface. Part of the light will be refracted into the surface. Describe how you would do an experiment to determine the polarization of the refracted light. What direction would you expect the polarization to have and would you expect it to be 100?
27.9: *Extended Topic* Microscopy Enhanced by the Wave Characteristics of Light
37. Explain how microscopes can use wave optics to improve contrast and why this is important.
38. A bright white light under water is collimated and directed upon a prism. What range of colors does one see emerging?
Problems & Exercises
27.1: The Wave Aspect of Light: Interference
39. Show that when light passes from air to water, its wavelength decreases to 0.750 times its original value.
Solution
1/1.333 = 0.750
40. Find the range of visible wavelengths of light in crown glass.
41. What is the index of refraction of a material for which the wavelength of light is 0.671 times its value in a vacuum? Identify the likely substance.
Solution
1.49, Polystyrene
42. Analysis of an interference effect in a clear solid shows that the wavelength of light in the solid is 329 nm. Knowing this light comes from a He-Ne laser and has a wavelength of 633 nm in air, is the substance zircon or diamond?
43. What is the ratio of thicknesses of crown glass and water that would contain the same number of wavelengths of light?
Solution
0.877 glass to water
27.3: Young’s Double Slit Experiment
44. At what angle is the first-order maximum for 450-nm wavelength blue light falling on double slits separated by 0.0500 mm?
Solution
0.516∘
45. Calculate the angle for the third-order maximum of 580-nm wavelength yellow light falling on double slits separated by 0.100 mm.
46. What is the separation between two slits for which 610-nm orange light has its first maximum at an angle of 30.0∘?
Solution
1.22×10−6m
47. Find the distance between two slits that produces the first minimum for 410-nm violet light at an angle of 45.0∘.
48. Calculate the wavelength of light that has its third minimum at an angle of 30.0∘ when falling on double slits separated by 3.00μm Explicitly, show how you follow the steps in "Problem-Solving Strategies for Wave Optics."
Solution
600nm
49. What is the wavelength of light falling on double slits separated by 2.00μm if the third-order maximum is at an angle of 60.0∘?
50. At what angle is the fourth-order maximum for the situation in the first exercise?
Solution
2.06∘
51. What is the highest-order maximum for 400-nm light falling on double slits separated by 25.0μm?
52. Find the largest wavelength of light falling on double slits separated by 1.20μm for which there is a first-order maximum. Is this in the visible part of the spectrum?
Solution
1200 nm (not visible)
53. What is the smallest separation between two slits that will produce a second-order maximum for 720-nm red light?
54. (a) What is the smallest separation between two slits that will produce a second-order maximum for any visible light?
(b) For all visible light?
Solution
(a) 760 nm
(b) 1520 nm
55. (a) If the first-order maximum for pure-wavelength light falling on a double slit is at an angle of 10.0∘, at what angle is the second-order maximum?
(b) What is the angle of the first minimum?
(c) What is the highest-order maximum possible here?
56. The figure shows a double slit located a distance x from a screen, with the distance from the center of the screen given by y. When the distance d between the slits is relatively large, there will be numerous bright spots, called fringes. Show that, for small angles (where sinθ≈θ, with θ in radians), the distance between fringes is given by δy=xλ/d.
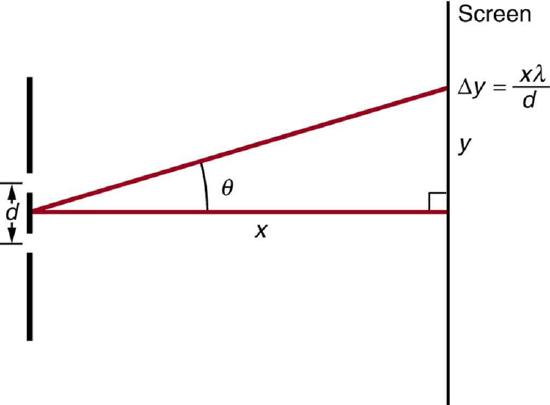
The distance between adjacent fringes is δy=xλ/d, assuming the slit separation d is large compared with λ.
Solution
For small angles sinθ−tanθ≈θ(inradians).
For two adjacent fringes we have, dsinθm=mλ and dsinθm+1=(m+1)λ Subtracting these equations gives d(sinθm+1−sinθm)=[(m+1)−m]λ d(θm+1−θm)=λ tanθm=ymx≈θm→d(ym+1x−ymx)=λ dδyx=λ→δy=xλd
57. Using the result of the problem above, calculate the distance between fringes for 633-nm light falling on double slits separated by 0.0800 mm, located 3.00 m from a screen as in Figure 8.
58. Using the result of the problem two problems prior, find the wavelength of light that produces fringes 7.50 mm apart on a screen 2.00 m from double slits separated by 0.120 mm (see Figure 8).
Solution
450 nm
27.4: Multiple Slit Diffraction
59. A diffraction grating has 2000 lines per centimeter. At what angle will the first-order maximum be for 520-nm-wavelength green light?
Solution
5.97∘
60. Find the angle for the third-order maximum for 580-nm-wavelength yellow light falling on a diffraction grating having 1500 lines per centimeter.
61. How many lines per centimeter are there on a diffraction grating that gives a first-order maximum for 470-nm blue light at an angle of 25.0∘?
Solution
8.99×103
62. What is the distance between lines on a diffraction grating that produces a second-order maximum for 760-nm red light at an angle of 60.0∘?
63. Calculate the wavelength of light that has its second-order maximum at 45.0∘ when falling on a diffraction grating that has 5000 lines per centimeter.
Solution
707 nm
64. An electric current through hydrogen gas produces several distinct wavelengths of visible light. What are the wavelengths of the hydrogen spectrum, if they form first-order maxima at angles of 24.2∘, 25.7∘, 29.1∘, and 41.0∘ when projected on a diffraction grating having 10,000 lines per centimeter? Explicitly show how you follow the steps in "Problem-Solving Strategies for Wave Optics."
65. (a) What do the four angles in the above problem become if a 5000-line-per-centimeter diffraction grating is used?
(b) Using this grating, what would the angles be for the second-order maxima?
(c) Discuss the relationship between integral reductions in lines per centimeter and the new angles of various order maxima.
Solution
(a) 11.8∘, 12.5∘, 14.1∘, 19.2∘
(b) 24.2∘, 25.7∘, 29.1∘, 41.0∘
(c) Decreasing the number of lines per centimeter by a factor of x means that the angle for the x‐order maximum is the same as the original angle for the first- order maximum.
66. What is the maximum number of lines per centimeter a diffraction grating can have and produce a complete first-order spectrum for visible light?
67. The yellow light from a sodium vapor lamp seems to be of pure wavelength, but it produces two first-order maxima at 36.093∘ and 36.129∘ when projected on a 10,000 line per centimeter diffraction grating. What are the two wavelengths to an accuracy of 0.1 nm?
Solution
589.1 nm and 589.6 nm
68. What is the spacing between structures in a feather that acts as a reflection grating, given that they produce a first-order maximum for 525-nm light at a 30.0∘ angle?
69. Structures on a bird feather act like a reflection grating having 8000 lines per centimeter. What is the angle of the first-order maximum for 600-nm light?
Solution
28.7∘
70. An opal such as that shown in Figure 2 acts like a reflection grating with rows separated by about 8μm. If the opal is illuminated normally,
(a) at what angle will red light be seen and
(b) at what angle will blue light be seen?
71. At what angle does a diffraction grating produces a second-order maximum for light having a first-order maximum at 20.0∘?
Solution
43.2∘
72. Show that a diffraction grating cannot produce a second-order maximum for a given wavelength of light unless the first-order maximum is at an angle less than 30.0∘.
73. If a diffraction grating produces a first-order maximum for the shortest wavelength of visible light at 30.0∘, at what angle will the first-order maximum be for the longest wavelength of visible light?
Solution
90.0∘
74. (a) Find the maximum number of lines per centimeter a diffraction grating can have and produce a maximum for the smallest wavelength of visible light.
(b) Would such a grating be useful for ultraviolet spectra?
(c) For infrared spectra?
75. (a) Show that a 30,000-line-per-centimeter grating will not produce a maximum for visible light.
(b) What is the longest wavelength for which it does produce a first-order maximum?
(c) What is the greatest number of lines per centimeter a diffraction grating can have and produce a complete second-order spectrum for visible light?
Solution
(a) The longest wavelength is 333.3 nm, which is not visible.
(b) 333 nm (UV)
(c) 6.58×103cm
76. A He–Ne laser beam is reflected from the surface of a CD onto a wall. The brightest spot is the reflected beam at an angle equal to the angle of incidence. However, fringes are also observed. If the wall is 1.50 m from the CD, and the first fringe is 0.600 m from the central maximum, what is the spacing of grooves on the CD?
77. The analysis shown in the figure below also applies to diffraction gratings with lines separated by a distance d. What is the distance between fringes produced by a diffraction grating having 125 lines per centimeter for 600-nm light, if the screen is 1.50 m away?
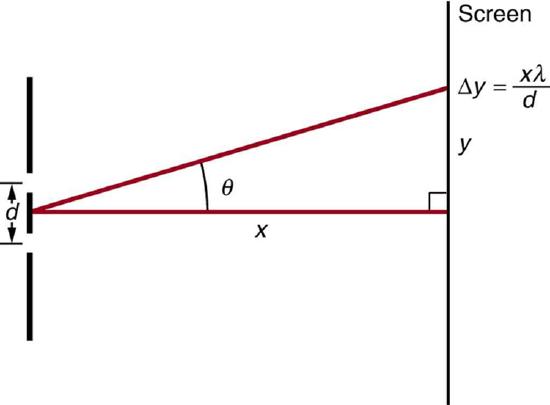
The distance between adjacent fringes is δy=xλ/d, assuming the slit separation d is large compared with λ.
Solution
1.13×10−2m
78. Unreasonable Results:
Red light of wavelength of 700 nm falls on a double slit separated by 400 nm.
(a) At what angle is the first-order maximum in the diffraction pattern?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
79. Unreasonable Results:
(a) What visible wavelength has its fourth-order maximum at an angle of 25.0∘ when projected on a 25,000-line-per-centimeter diffraction grating?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
Solution
(a) 42.3 nm
(b) Not a visible wavelength
(c) The number of slits in this diffraction grating is too large. Etching in integrated circuits can be done to a resolution of 50 nm, so slit separations of 400 nm are at the limit of what we can do today. This line spacing is too small to produce diffraction of light.
80. Construct Your Own Problem:
Consider a spectrometer based on a diffraction grating. Construct a problem in which you calculate the distance between two wavelengths of electromagnetic radiation in your spectrometer. Among the things to be considered are the wavelengths you wish to be able to distinguish, the number of lines per meter on the diffraction grating, and the distance from the grating to the screen or detector. Discuss the practicality of the device in terms of being able to discern between wavelengths of interest.
27.5: Single Slit Diffraction
81. (a) At what angle is the first minimum for 550-nm light falling on a single slit of width 1.00μm?
(b) Will there be a second minimum?
Solution
(a) 33.4∘
(b) No
82. (a) Calculate the angle at which a 2.00−μm-wide slit produces its first minimum for 410-nm violet light.
(b) Where is the first minimum for 700-nm red light?
83. (a) How wide is a single slit that produces its first minimum for 633-nm light at an angle of 28.0∘?
(b) At what angle will the second minimum be?
Solution
(a) 1.35×10−6m
(b) 69.9∘
84. (a) What is the width of a single slit that produces its first minimum at 60.0∘ for 600-nm light?
(b) Find the wavelength of light that has its first minimum at 62.0∘.
85. Find the wavelength of light that has its third minimum at an angle of 48.6∘ when it falls on a single slit of width 3.00μm.
Solution
750 nm
86. Calculate the wavelength of light that produces its first minimum at an angle of 36.9∘ when falling on a single slit of width 1.00μm.
87. (a) Sodium vapor light averaging 589 nm in wavelength falls on a single slit of width 7.50μm. At what angle does it produces its second minimum?
(b) What is the highest-order minimum produced?
Solution
(a) 9.04∘
(b) 12
88. (a) Find the angle of the third diffraction minimum for 633-nm light falling on a slit of width 20.0μm.
(b) What slit width would place this minimum at 85.0∘? Explicitly show how you follow the steps in "Problem-Solving Strategies fro Wave Optics."
89. (a) Find the angle between the first minima for the two sodium vapor lines, which have wavelengths of 589.1 and 589.6 nm, when they fall upon a single slit of width 2.00μm.
(b) What is the distance between these minima if the diffraction pattern falls on a screen 1.00 m from the slit?
(c) Discuss the ease or difficulty of measuring such a distance.
Solution
(a) 0.0150∘
(b) 0.262 mm
(c) This distance is not easily measured by human eye, but under a microscope or magnifying glass it is quite easily measurable.
90. (a) What is the minimum width of a single slit (in multiples of λ) that will produce a first minimum for a wavelength λ?
(b) What is its minimum width if it produces 50 minima?
(c) 1000 minima?
91. (a) If a single slit produces a first minimum at 14.5∘, at what angle is the second-order minimum?
(b) What is the angle of the third-order minimum?
(c) Is there a fourth-order minimum?
(d) Use your answers to illustrate how the angular width of the central maximum is about twice the angular width of the next maximum (which is the angle between the first and second minima).
Solution
(a) 30.1∘
(b) 48.7∘
(c) No
(d) 2θ1=(2)(14.5∘)=29∘,θ2−θ1=30.05∘−14.5∘=15.56∘. Thus, 29∘≈(2)(15.56∘)=31.1∘.
92. A double slit produces a diffraction pattern that is a combination of single and double slit interference. Find the ratio of the width of the slits to the separation between them, if the first minimum of the single slit pattern falls on the fifth maximum of the double slit pattern. (This will greatly reduce the intensity of the fifth maximum.)
93. Integrated Concepts:
A water break at the entrance to a harbor consists of a rock barrier with a 50.0-m-wide opening. Ocean waves of 20.0-m wavelength approach the opening straight on. At what angle to the incident direction are the boats inside the harbor most protected against wave action?
Solution
23.6∘,53.1∘
94. Integrated Concepts:
An aircraft maintenance technician walks past a tall hangar door that acts like a single slit for sound entering the hangar. Outside the door, on a line perpendicular to the opening in the door, a jet engine makes a 600-Hz sound. At what angle with the door will the technician observe the first minimum in sound intensity if the vertical opening is 0.800 m wide and the speed of sound is 340 m/s?
27.6: Limits of Resolution: The Rayleigh Criterion
95. The 300-m-diameter Arecibo radio telescope pictured in Figure 4 detects radio waves with a 4.00 cm average wavelength.
(a) What is the angle between two just-resolvable point sources for this telescope?
(b) How close together could these point sources be at the 2 million light year distance of the Andromeda galaxy?
Solution
(a) 1.63×10−4rad
(b) 326 ly
96. Assuming the angular resolution found for the Hubble Telescope in the "Calculating Diffraction Limits of the Hubble Space Telescope" example, what is the smallest detail that could be observed on the Moon?
97. Diffraction spreading for a flashlight is insignificant compared with other limitations in its optics, such as spherical aberrations in its mirror. To show this, calculate the minimum angular spreading of a flashlight beam that is originally 5.00 cm in diameter with an average wavelength of 600 nm.
Solution
1.46×10−5rad
98. (a) What is the minimum angular spread of a 633-nm wavelength He-Ne laser beam that is originally 1.00 mm in diameter?
(b) If this laser is aimed at a mountain cliff 15.0 km away, how big will the illuminated spot be?
(c) How big a spot would be illuminated on the Moon, neglecting atmospheric effects? (This might be done to hit a corner reflector to measure the round-trip time and, hence, distance.) Explicitly show how you follow the steps in "Problem-Solving Strategies for Wave Optics."
99. A telescope can be used to enlarge the diameter of a laser beam and limit diffraction spreading. The laser beam is sent through the telescope in opposite the normal direction and can then be projected onto a satellite or the Moon.
(a) If this is done with the Mount Wilson telescope, producing a 2.54-m-diameter beam of 633-nm light, what is the minimum angular spread of the beam?
(b) Neglecting atmospheric effects, what is the size of the spot this beam would make on the Moon, assuming a lunar distance of 3.84×108m?
Solution
(a) 3.04×10−7rad
(b) diameter of 235 m
100. The limit to the eye’s acuity is actually related to diffraction by the pupil.
(a) What is the angle between two just-resolvable points of light for a 3.00-mm-diameter pupil, assuming an average wavelength of 550 nm?
(b) Take your result to be the practical limit for the eye. What is the greatest possible distance a car can be from you if you can resolve its two headlights, given they are 1.30 m apart?
(c) What is the distance between two just-resolvable points held at an arm’s length (0.800 m) from your eye?
(d) How does your answer to (c) compare to details you normally observe in everyday circumstances?
101. What is the minimum diameter mirror on a telescope that would allow you to see details as small as 5.00 km on the Moon some 384,000 km away? Assume an average wavelength of 550 nm for the light received.
Solution
5.15 cm
102. You are told not to shoot until you see the whites of their eyes. If the eyes are separated by 6.5 cm and the diameter of your pupil is 5.0 mm, at what distance can you resolve the two eyes using light of wavelength 555 nm?
103. (a) The planet Pluto and its Moon Charon are separated by 19,600 km. Neglecting atmospheric effects, should the 5.08-m-diameter Mount Palomar telescope be able to resolve these bodies when they are 4.50×109km from Earth? Assume an average wavelength of 550 nm.
(b) In actuality, it is just barely possible to discern that Pluto and Charon are separate bodies using an Earth-based telescope. What are the reasons for this?
Solution
(a) Yes. Should easily be able to discern.
(b) The fact that it is just barely possible to discern that these are separate bodies indicates the severity of atmospheric aberrations.
104. The headlights of a car are 1.3 m apart. What is the maximum distance at which the eye can resolve these two headlights? Take the pupil diameter to be 0.40 cm.
105. When dots are placed on a page from a laser printer, they must be close enough so that you do not see the individual dots of ink. To do this, the separation of the dots must be less than Raleigh’s criterion. Take the pupil of the eye to be 3.0 mm and the distance from the paper to the eye of 35 cm; find the minimum separation of two dots such that they cannot be resolved. How many dots per inch (dpi) does this correspond to?
106. Unreasonable Results:
An amateur astronomer wants to build a telescope with a diffraction limit that will allow him to see if there are people on the moons of Jupiter.
a) What diameter mirror is needed to be able to see 1.00 m detail on a Jovian Moon at a distance of 7.50×108km from Earth? The wavelength of light averages 600 nm.
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
107. Construct Your Own Problem:
Consider diffraction limits for an electromagnetic wave interacting with a circular object. Construct a problem in which you calculate the limit of angular resolution with a device, using this circular object (such as a lens, mirror, or antenna) to make observations. Also calculate the limit to spatial resolution (such as the size of features observable on the Moon) for observations at a specific distance from the device. Among the things to be considered are the wavelength of electromagnetic radiation used, the size of the circular object, and the distance to the system or phenomenon being observed.
27.7: Thin Film Interference
108. A soap bubble is 100 nm thick and illuminated by white light incident perpendicular to its surface. What wavelength and color of visible light is most constructively reflected, assuming the same index of refraction as water?
Solution
532 nm (green)
109. An oil slick on water is 120 nm thick and illuminated by white light incident perpendicular to its surface. What color does the oil appear (what is the most constructively reflected wavelength), given its index of refraction is 1.40?
110. Calculate the minimum thickness of an oil slick on water that appears blue when illuminated by white light perpendicular to its surface. Take the blue wavelength to be 470 nm and the index of refraction of oil to be 1.40.
Solution
83.9 nm
111. Find the minimum thickness of a soap bubble that appears red when illuminated by white light perpendicular to its surface. Take the wavelength to be 680 nm, and assume the same index of refraction as water.
112. A film of soapy water (n=1.33) on top of a plastic cutting board has a thickness of 233 nm. What color is most strongly reflected if it is illuminated perpendicular to its surface?
Solution
620 nm (orange)
113. What are the three smallest non-zero thicknesses of soapy water (n=1.33) on Plexiglas if it appears green (constructively reflecting 520-nm light) when illuminated perpendicularly by white light? Explicitly show how you follow the steps in Problem Solving Strategies for Wave Optics.
114. Suppose you have a lens system that is to be used primarily for 700-nm red light. What is the second thinnest coating of fluorite (magnesium fluoride) that would be non-reflective for this wavelength?
Solution
380 nm
115. (a) As a soap bubble thins it becomes dark, because the path length difference becomes small compared with the wavelength of light and there is a phase shift at the top surface. If it becomes dark when the path length difference is less than one-fourth the wavelength, what is the thickest the bubble can be and appear dark at all visible wavelengths? Assume the same index of refraction as water.
(b) Discuss the fragility of the film considering the thickness found.
116. A film of oil on water will appear dark when it is very thin, because the path length difference becomes small compared with the wavelength of light and there is a phase shift at the top surface. If it becomes dark when the path length difference is less than one-fourth the wavelength, what is the thickest the oil can be and appear dark at all visible wavelengths? Oil has an index of refraction of 1.40.
Solution
33.9 nm
117. Figure shows two glass slides illuminated by pure-wavelength light incident perpendicularly. The top slide touches the bottom slide at one end and rests on a 0.100-mm-diameter hair at the other end, forming a wedge of air.
(a) How far apart are the dark bands, if the slides are 7.50 cm long and 589-nm light is used?
(b) Is there any difference if the slides are made from crown or flint glass? Explain.
118. Figure in Exercise 117 shows two 7.50-cm-long glass slides illuminated by pure 589-nm wavelength light incident perpendicularly. The top slide touches the bottom slide at one end and rests on some debris at the other end, forming a wedge of air. How thick is the debris, if the dark bands are 1.00 mm apart?
Solution
4.42×10−5m
119. Repeat Exercise, but take the light to be incident at a 45º angle.
120. Repeat Exercise, but take the light to be incident at a 45º angle.
Solution
The oil film will appear black, since the reflected light is not in the visible part of the spectrum.
121. Unreasonable Results
To save money on making military aircraft invisible to radar, an inventor decides to coat them with a non-reflective material having an index of refraction of 1.20, which is between that of air and the surface of the plane. This, he reasons, should be much cheaper than designing Stealth bombers.
(a) What thickness should the coating be to inhibit the reflection of 4.00-cm wavelength radar?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
27.8: Polarization
122. What angle is needed between the direction of polarized light and the axis of a polarizing filter to cut its intensity in half?
Solution
45.0º
123. The angle between the axes of two polarizing filters is 45.0º. By how much does the second filter reduce the intensity of the light coming through the first?
124. If you have completely polarized light of intensity 150W/m2, what will its intensity be after passing through a polarizing filter with its axis at an 89.0º angle to the light’s polarization direction?
Solution
45.7mW/m2
125. What angle would the axis of a polarizing filter need to make with the direction of polarized light of intensity 1.00kW/m2 to reduce the intensity to 10.0W/m2?
126. At the end of Example, it was stated that the intensity of polarized light is reduced to 90.0% of its original value by passing through a polarizing filter with its axis at an angle of 18.4º to the direction of polarization. Verify this statement.
Solution
90.0%
127. Show that if you have three polarizing filters, with the second at an angle of 45º to the first and the third at an angle of 90.0º to the first, the intensity of light passed by the first will be reduced to 25.0% of its value. (This is in contrast to having only the first and third, which reduces the intensity to zero, so that placing the second between them increases the intensity of the transmitted light.)
128. Prove that, if I is the intensity of light transmitted by two polarizing filters with axes at an angle θ and I′ is the intensity when the axes are at an angle 90.0º−θ, then I+I′=I0, the original intensity. (Hint: Use the trigonometric identities cos(90.0º−θ)=sinθ and cos2θ+sin2θ=1.)
Solution
I0
129. At what angle will light reflected from diamond be completely polarized?
130. What is Brewster’s angle for light traveling in water that is reflected from crown glass?
Solution
48.8º
131. A scuba diver sees light reflected from the water’s surface. At what angle will this light be completely polarized?
132. At what angle is light inside crown glass completely polarized when reflected from water, as in a fish tank?
Solution
41.2º
133. Light reflected at 55.6º from a window is completely polarized. What is the window’s index of refraction and the likely substance of which it is made?
134. (a) Light reflected at 62.5º from a gemstone in a ring is completely polarized. Can the gem be a diamond?
(b) At what angle would the light be completely polarized if the gem was in water?
Solution
(a) 1.92, not diamond (Zircon)
(b) 55.2º
135. If θb is Brewster’s angle for light reflected from the top of an interface between two substances, and θ′b is Brewster’s angle for light reflected from below, prove that θb+θ′b=90.0º.
136. Integrated Concepts
If a polarizing filter reduces the intensity of polarized light to 50.0 of its original value, by how much are the electric and magnetic fields reduced?
Solution
B2=0.707B1
137. Integrated Concepts
Suppose you put on two pairs of Polaroid sunglasses with their axes at an angle of 15.0º. How much longer will it take the light to deposit a given amount of energy in your eye compared with a single pair of sunglasses? Assume the lenses are clear except for their polarizing characteristics.
138. Integrated Concepts
(a) On a day when the intensity of sunlight is 1.00kW/m2, a circular lens 0.200 m in diameter focuses light onto water in a black beaker. Two polarizing sheets of plastic are placed in front of the lens with their axes at an angle of 20.0º. Assuming the sunlight is unpolarized and the polarizers are 100 efficient, what is the initial rate of heating of the water in ºC/s, assuming it is 80.0 absorbed? The aluminum beaker has a mass of 30.0 grams and contains 250 grams of water.
(b) Do the polarizing filters get hot? Explain.
Solution
(a) 2.07×10−2°C/s
(b) Yes, the polarizing filters get hot because they absorb some of the lost energy from the sunlight.
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

