1.21: Hot and Cold Relics of the Big Bang
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the previous chapter we worked out the abundance of a massive fermionic particles species, χ and antiparticle ˉχ under a particular set of assumptions including kinetic equilibrium as well as chemical equilibrium maintained by reactions that set the chemical potentials μχ=μˉχ=0. We saw that, given these assumptions, if we artificially set the initial values of nχ and nˉχ to zero we would, at early times when mχc2≪kBT, rapidly evolve to an abundance of them very similar to that of the photons -- only differing by the number of degrees of freedom, g, and the slight difference that arises due to the small difference in the form of f for fermionic and bosonic species. As long as all our assumptions remain valid, the abundance of the species would eventually start to decrease as kBT dropped below mχc2, suppressed by the Boltzmann factor exp(−mχc2/(kBT)). In this scenario, assuming that today mχc2≫kBT, we would have negligible amounts of these particles still around today.
Particles that at one time were driven to kinetic and chemical equilibrium abundances in the big bang, and survive to today are called "thermal relics." Survival to today sometimes require a departure from the equilibrium abundances worked out in the previous chapter. These departures, in some cases, occur because the reactions that maintained chemical equilibrium become too slow to continue to do so as the temperature drops and the equilibrium abundance changes. We refer to the process of the reactions becoming slow as "freeze-out." If freeze-out happens when the particles are still relativistic we call them "hot relics," if it occurs when they are non-relativistic we call them "cold relics." In this chapter we discuss hot and cold relics of the big bang.
Freeze-out
Calculation of reaction rates, and a complete treatment of non-equilibrium abundance evolution, is beyond the scope of this course. Here we summarize some important results:
- When per-particle reaction rates, Γ, are much greater than the expansion rate, H, then the abundance is rapidly driven to an equilibrium amount with chemical potentials governed by the reactions in question.
- The ratio Γ/H in general decreases over time as the universe expands and therefore temperature and density drops. Thus reactions tend to go from being "fast" (able to maintain equilibrium) to being "slow" (not able to maintain equilibrium). Note that both H and Γ drop with time, but Γ usually drops more rapidly.
- When Γ<<H for reactions that create and destroy χ and ˉχ particles then it is a good approximation to ignore these processes and assume their numbers just dilute with the expansion. We therefore have nχ∝a−3 and nˉχ∝a−3.
- In fact, a fairly good approximation is to define a freeze-out temperature TF to be the temperature at which Γ=H and then assume the equilibrium abundance for T>TF and nχ∝a−3 for T<TF, with the proportionality constant chosen so as to have a continuous abundance curve at T=TF.
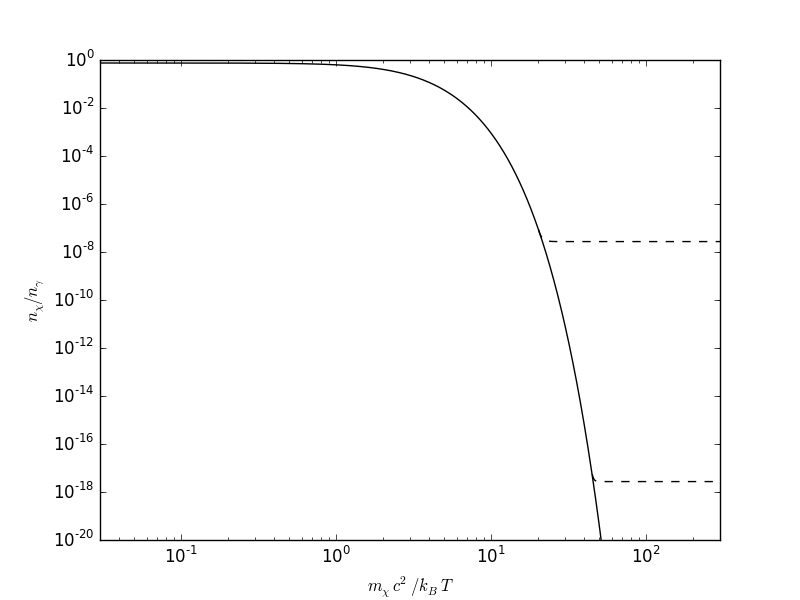 |
| Solid curve: Equilibrium abundance for a massive fermionic species with g=2 and zero chemical potential relative to massless bosonic species with g=2. This is very similar to what you were asked to sketch in the previous chapter since nγ∝a−3. Dashed curves: the same ratio for two cold relics over time, with differing values of TF. These are considered cold relics since they freeze out at mχc2>kBT. Note that the later the occurrence of freeze-out, the lower the relic abundance. Not shown: hot relics, which would freeze out at T<TF. Note that for hot relics the relic abundance is independent of when freeze-out occurs since the equilibrium curve is flat there. |
Hot Relics: Photons and Neutrinos
At z>107 or so, corresponding to temperatures greater than about kBT=4 keV reactions such as
e−+p+←→e−+p++γ
that create or destroy photons become slow. Since this happens while photons are relativistic (since photons are always relativistic), photons qualify as hot relics. This is the relic background predicted by Alpher and Herman in the 1940s and serendipitously discovered by Penzias and Wilson in 1964. We know it today as the cosmic microwave background (CMB). With a temperature of about 2.73∘K the intensity of this light peaks in the microwave region of the spectrum. The spectrum has been measured with high precision and found to be consistent with a black body.
Various different types of distortion away from black body have been constrained by these measurements, including a non-zero chemical potential. Using data from the FIRAS instrument on the COBE satellite, cosmologists have placed a limit of μ/(kBT)<10−5. This level of consistency with a black body spectrum places constraints on possible scenarios in which energy is injected into the plasma of the big bang, for example from some particle species that decays while out of equilibrium into two photons. Such injection of energy would heat up the plasma. If the energy injection occurred at z>107, the photon-number-changing reactions would ensure that the chemical potential remained zero, with the result that we would see no evidence in the spectrum of the CMB today. If the energy injection occurred at lower redshifts then the lack of photon-number-changing reactions would lead to a non-zero chemical potential. With a sufficient amount of energy injected, this distortion of the spectrum away from that of a black body would be discernible with current data.
Neutrinos are subatomic particles first inferred from examination of radioactive decay products. For example, a free neutron will decay to an electron, a proton and a neutrino. If one measures the momentum of the electron and proton from a neutron decaying at rest, one finds that either energy and momentum conservation is violated, or there must be an unseen additional decay product: the neutrino. There are three types of neutrinos in the standard model of particle physics, one paired with each of the three charged leptons in the standard model. Together these are the electron and the electron neutrino, the muon and the muon neutrino, and the tauon and the tau neutrino.
Unlike the charged leptons, which interact with other particles via both the weak and electromagnetic forces, neutrinos only interact via the weak force. This force is appropriately named: the weak interactions are very weak. Neutrinos produced in nuclear reactions in the sun stream straight out of the sun hardly interacting at all, whereas photons produced in nuclear reactions scatter around the plasma of the sun for millions of years before finally making it to the surface. Despite the weakness of the interactions, at sufficiently early times the universe was hot and dense enough that reactions that produce and destroy neutrinos were occurring rapidly, as well as neutrino scattering reactions that exchange kinetic energy. The universe was in this state at temperatures kBT>0.8 MeV. Neutrinos were highly relativistic at this time, and thus they qualify as hot relics.
We have strong indirect indications of the existence of a relic background of cosmic neutrinos. Due to the weakness of their interactions, their low energy today (having been cooled by the expansion), and the drop in reaction rates with energy, it is exceedingly difficult, and perhaps practically impossible, to directly detect the cosmic neutrino background.
When we study Big Bang Nucleosynthesis (BBN) we will see some of the indirect evidence for the neutrino background. The energy density of the cosmic neutrino background, ϵν, contributes to the total energy density and thus, via the Friedmann equation, to the expansion rate. The existence of the neutrinos means that, at a given temperature, the expansion rate is faster than it would be otherwise. We will see that this increased expansion rate affects the abundances of light elements. We will study the case of helium-4 in particular.
I have a particular interest in neutrinos and the cosmic neutrino background. The neutrinos have a somewhat-unique influence on the oscillations of standing waves in the plasma of the big bang, which follows from the fact that they can stream through the plasma at the speed of light, unlike the photons that readily scatter off of free electrons. A result of this free-streaming is that gravitational potentials that drive the standing wave oscillations decay more rapidly than they would otherwise, fast enough that they alter the temporal phases of the oscillations, an effect that is observable in the statistical properties of the cosmic microwave background. My graduate students and I were the first to isolate this effect in the data. The paper is in Physical Review Letters. There is a popular account in Scientific American, and in some blog posts including this one, and this one which is somewhat overblown about the significance, but provides, as background material, a nice summary of our historical progress on understanding the big bang. The work also led to an article about me and my research and teaching in the Sacramento Bee.
Box 1.21.1
Exercise 21.1.1: At z≃107 some reactions involving photons became slow, and at z≃103 some other reactions involving photons became slow. Which epoch corresponds to freeze-out for photons? What is the significance of the later epoch?
Exercise 21.1.2: A weaker interaction (slower production and annihilation rates) usually means freeze-out happens earlier or later?
Exercise 21.1.3: For hot relics, why is the abundance today relatively insensitive to freeze-out temperature?
Exercise 21.1.4: Why do additional species of light particles potentially lead to a faster expansion rate in the early universe at a given temperature?
Cold Relics: The WIMP Miracle (or Misleading Coincidence?)
We've learned so far that photons and neutrinos are produced thermally in the big bang. Potentially there are also particles produced in the big bang that are not in the standard model of particle physics. The cold dark matter that seems to dominate the mass density of the universe might be such a particle. Here we consider a general class of models of dark matter in which it is a Weakly Interacting Massive Particle (WIMP).
WIMPs have received a lot of attention. There are major experimental efforts underway to detect WIMPs indirectly (by seeing evidence of their annihilation into standard model decay products in regions of dense dark matter such as the galactic center or centers of dwarf galaxies) to detect them directly (via rare interactions of dark matter with baryonic matter in a sensitive detector), and to produce them in particle colliders such as the Large Hadron Collider in Europe.
This attention follows, at least in part, from a theoretical result called the "WIMP Miracle." The miracle is as follows. An idea in particle physics called "supersymmetry," which is attractive to particle physics because of problems it solves having nothing to do with cosmological observations, leads to a collection of new particles, one of which could quite naturally turn out to be the dark matter. If one works out reaction rates for these supersymmetric particles, and when freeze-out occurs for the lightest one (which is the only stable one), the lightest one can easily have (depending on choices of free parameters) the right relic abundance today. More generally, supersymmetry offers a solution to the "hierarchy" problem of particle physics, a problem associated with the weak interaction scale. Weak interaction particle cross sections are about what one needs in order to end up with relic abundances today roughly consistent with the mass density of dark matter as inferred from cosmological observations.
What is the relationship between particle cross sections and their relic abundance? Particle interaction cross sections control reaction rates. The smaller the cross sections, the slower the reaction rates. The slower the reaction rates, the earlier freeze-out occurs. The earlier freeze-out occurs (not in terms of time itself, but in terms of the time-like variable mχc2/(kBT)), the higher the resulting abundance. A weak interaction level of cross section (which the supersymmetric particles generally have) turns out to be just right for getting the right density of dark matter today. This is the WIMP miracle.
Or... it could be just a coincidence that has thrown us off the right path toward finding out what the dark matter really is. So far, searches for supersymmmetric dark matter, after decades of searching and improving sensitivity, have resulted in upper limits. There are some claimed detections, but none of these have yet been reproduced by other experiments.
Box 1.21.2
Exercise 21.21: For cold relics, why are weaker interactions associated with higher relic abundances?
Exercise 21.2.2: If there is a new particle physics theory that has in it new particles, or new interactions, or both, why is it important to consider cosmological consequences? What might they be?
Homework
21.1: Starting when kBT≃0.511 MeV, (so that mec2/(kBT)=1 ) the number density of electrons and positrons, relative to photons, begins to drop. Eventually, almost all the positrons and electrons are gone. This whole process occurs after the neutrinos have decoupled (at kBT=0.8 MeV) so the annihilations of the electrons and positrons all goes into heating up the photons (some goes into the remaining electrons and nuclei, but their number densities and kinetic energy densities are tiny compared to photon number an energy densities). Assuming that the process does not change the entropy in a comoving region, show that the end result is that neutrinos are cooler relative to photons by an amount
Tν/Tγ=(411)1/3.
You'll need to use the fact that the entropy density (physical density, not comoving density) for a relativistic species is
s=2π245gkB(kBTℏc)3
for bosons and
s=782π245gkB(kBTℏc)3
for fermions.
Some hints:
1) You have a conserved quantity. Evaluate it at a time when electrons and positrons are relativistic and at a later time when the electrons and positrons have all disappeared. Use this to figure out how the early temperature is related to the later temperature.
2) Since the neutrinos stop interacting with themselves and with electrons, positrons, and photons, their entropy is conserved separately from the electrons, positrons, and photons. The entropy of the electron, positron, and photon system is also conserved.
3) Electrons are spin 1/2 so have g=2. Same for positrons.
4) Initially neutrinos, electrons, positrons, and photons are exchanging kinetic energy and so their initial temperatures (prior to the electrons and positrons starting to disappear) are equal.
21.2: From atmospheric neutrino oscillations, we know that the lightest that the most massive neutrino can be is 0.048 eV/c2. Assuming it's as light as possible, what is a typical speed for the most massive neutrinos in the cosmic neutrino background today? (I'm looking for something correct to within a factor of 2 or so). Keep in mind that neutrinos freeze out while still relativistic so they keep f=[exp(pc/kBT)+1]−1 even though that is not equal to [exp(E/(kBT))+1]−1. For such a distribution a typical value of pc is kBT.
21.3: The number density of cosmic microwave background photons today is about 400/cm−3. Assuming there are 3 species of neutrino, each with g=2, and that their temperature is reduced relative to photons as described in problem 22.1, what is the number density of cosmic neutrinos today?
21.4: Combining results from 22.2 and 22.3, give an estimate of the number of highest-mass cosmic neutrinos flowing through you per second.
21.5: The baryon-to-photon ratio nb/nγ is about 6×10−10. Assuming, for simplicity, that all the baryons are protons, calculate the temperature at which there is one photon with energy above 13.6 eV for every baryon. You may use this result (which you could obtain by integrating over the photon energy distribution): the fraction of photons with energy above E is
n(>E)n≃(EkBT)2exp(−EkBT)
for E>>kBT.


