5.4.2: Field on the Axis of a Ring
- Page ID
- 8132
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
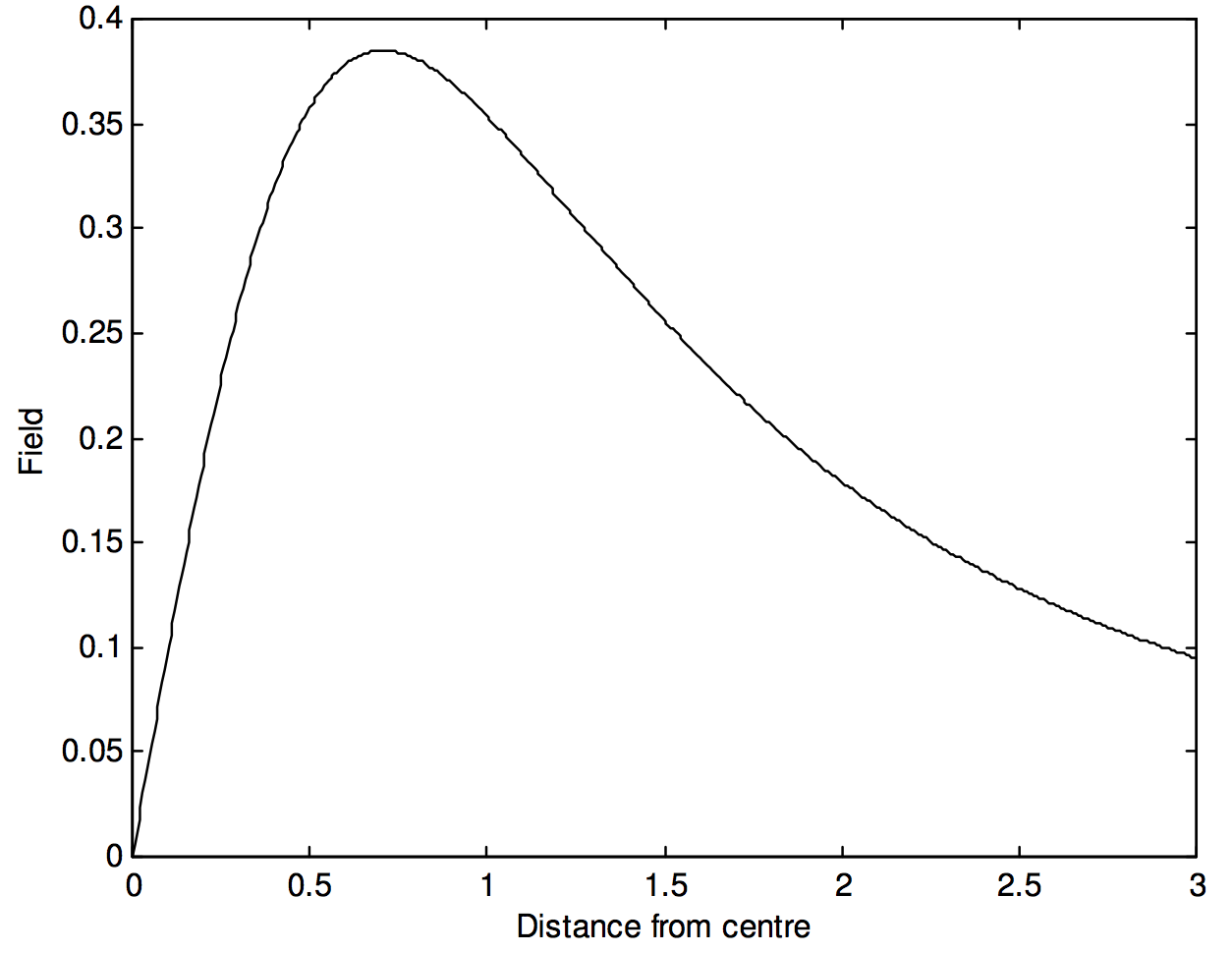
Before starting, one can obtain a qualitative idea of how the field on the axis of a ring varies with distance from the centre of the ring. Thus, the field at the centre of the ring will be zero, by symmetry. It will also be zero at an infinite distance along the axis. At other places it will not be zero; in other words, the field will first increase, then decrease, as we move along the axis. There will be some distance along the axis at which the field is greatest. We’ll want to know where this is, and what is its maximum value.
\(\text{FIGURE V.1}\)
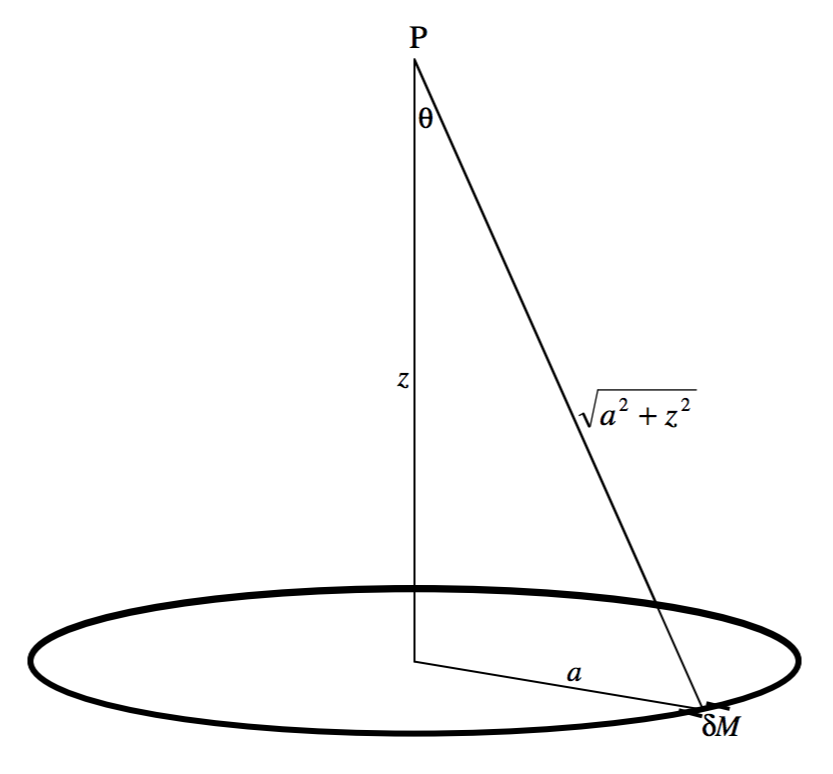
Figure V.1 shows a ring of mass \(M\), radius \(a\). The problem is to calculate the strength of the gravitational field at \(\text{P}\). We start by considering a small element of the ring of mass \(δM\). The contribution of this element to the field is
\[\frac{GδM}{a^2+z^2}, \]
directed from \(\text{P}\) towards \(δM\). This can be resolved into a component along the axis (directed to the centre of the ring) and a component at right angles to this. When the contributions to all elements around the circumference of the ring are added, the latter component will, by symmetry, be zero. The component along the axis of the ring is
\[\frac{GδM}{a^2+z^2} \cos θ = \frac{GδM}{a^2+z^2} \cdot \frac{z}{\sqrt{a^2 + z^2}} = \frac{GδM z}{\left( a^2 + z^2 \right)^{3/2}}. \]
On adding up the contributions of all elements around the circumference of the ring, we find, for the gravitational field at \(\text{P}\)
\[g = \frac{GMz}{\left( a^2 + z^2 \right)^{3/2}} \label{5.4.4} \tag{5.4.4}\]
directed towards the centre of the ring. This has the property, as expected, of being zero at the centre of the ring and at an infinite distance along the axis. If we express \(z\) in units of \(a\), and \(g\) in units of \(GM/a^2\), this becomes
\[g = \frac{z}{\left( 1 + z^2 \right)^{3/2}}. \label{5.4.5} \tag{5.4.5}\]
This is illustrated in figure V.2.
Excercise: Show that the field reaches its greatest value of \(\frac{\sqrt{12} GM}{9a^2} = \frac{0.385 GM}{a^2}\) where \(z = a/√2 = 0.707a\). Show that the field has half this maximum value where \(z = 0.2047a\) and \(z = 1.896a\).
\(\text{FIGURE V.2}\)