5.6: Calculating Surface Integrals
- Page ID
- 6817
While the concept of a surface integral sounds easy enough, how do we actually calculate one in practice? In this section I do two examples.
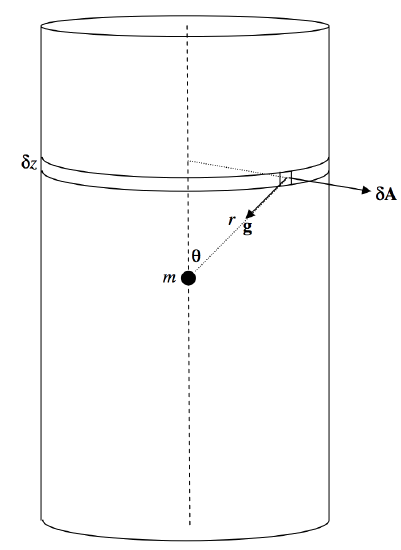
In Figure \(\text{V.19}\) I show a small mass \(m\), and I have surrounded it with a cylinder of radius \(a\) and height \(2h\). The problem is to calculate the surface integral \(∫ \textbf{g} \cdot d\textbf{A}\) through the entire surface of the cylinder. Of course we already know, from Gauss’s theorem, that the answer is \(= −4 \pi Gm\), but we would like to see a surface integral actually carried out.
\(\text{FIGURE V.19}\)
I have drawn a small element of the surface. Its area \(δA\) is \(dz\) times \(aδ \phi\), where \(\phi\) is the usual azimuthal angle of cylindrical coordinates. That is, \(δA = a \ δz \ δ\phi\). The magnitude \(g\) of the field there is \(Gm/r^2\), and the angle between \(\textbf{g}\) and \(d\textbf{A}\) is \(90^\circ + θ\). The outward flux through the small element is
\[\textbf{g} \cdot δ \textbf{A} = \frac{Gma \cos (θ+90^\circ) δz δ \phi}{r^2}.\]
(This is negative – i.e. it is actually an inward flux – because \(\cos (θ + 90^\circ ) = −\sin θ\).) When integrated around the elemental strip \(δz\), this is \(- \frac{2 \pi Gma \sin θ δz}{r^2}.\) To find the flux over the total curved surface, let’s integrate this from \(z = 0\) to \(h\) and double it, or, easier, from \(θ = \pi/2\) to \(α\) and double it, where \(\tan α = a/h\). We’ll need to express \(z\) and \(r\) in terms of \(θ\) (that’s easy:- \(z = a \cot θ\) and \(r = a \csc θ\)),and the integral becomes
\[4 \pi Gm \int_{\pi/2}^α \sin θ \ d θ = -4 \pi Gm \cos α \label{5.6.1} \tag{5.6.1}\]
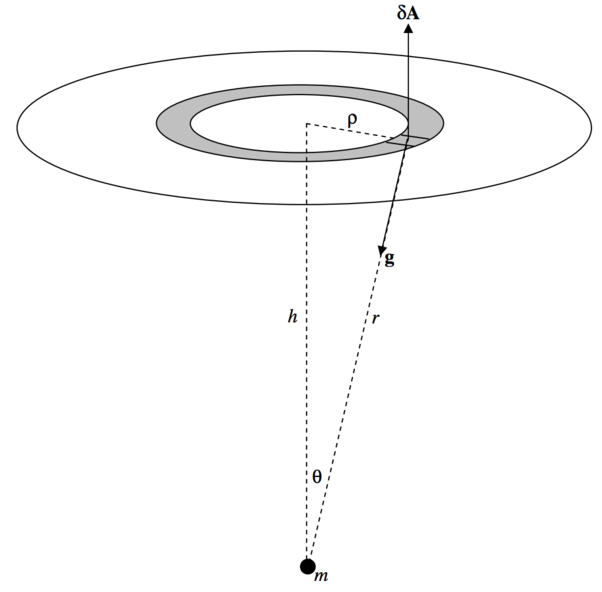
Let us now find the flux through one of the flat ends of the cylinder.
\(\text{FIGURE V.20}\)
This time, \(δA = ρ \ δρ \ δ\phi\), \(g = Gm/r^2\) and the angle between \(\textbf{g}\) and \(δ\textbf{A}\) is \(180^\circ − θ\). The outwards flux through the small element is \(\frac{Gmρ \cos (180^\circ - θ)δρδ\phi}{r^2}\) and when integrated around the annulus this becomes \(-\frac{2\pi Gm \cos θ \ ρδρ}{r^2}\). We now have to integrate this from \(ρ = 0\) to \(a\), or, better, from \(θ = 0\) to \(α\). We have \(r = h \sec θ\) and \(ρ = h \tan θ\), and the integral becomes
\[-2 \pi Gm \int_0^α \sin θ d θ = - 2\pi Gm (1- \cos α). \label{5.6.2} \tag{5.6.2}\]
There are two ends, so the total flux through the entire cylinder is twice this plus Equation \(\ref{5.6.1}\) to give
\[\phi = -4\pi Gm, \label{5.6.3} \tag{5.6.3}\]
as expected from Gauss’s theorem.
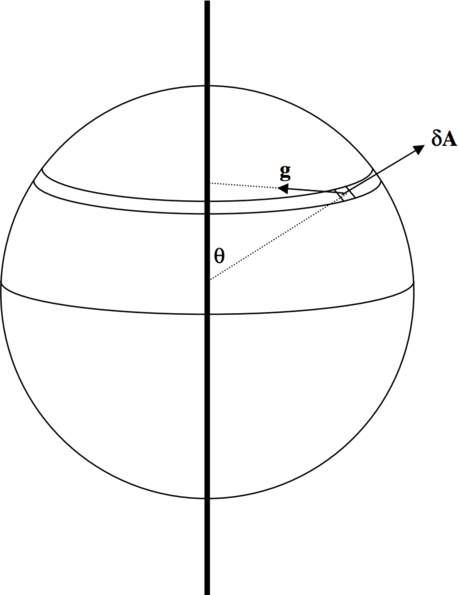
In figure \(\text{V.21}\) I have drawn (part of) an infinite rod whose mass per unit length is \(λ\). I have drawn around it a sphere of radius \(a\). The problem will be to determine the total normal flux through the sphere. From Gauss’s theorem, we know that the answer must be \(−8πGαλ\).
\(\text{FIGURE V.21}\)
The vector \(δ\textbf{A}\) representing the element of area is directed away from the centre of the sphere, and the vector \(\textbf{g}\) is directed towards the nearest point of the rod. The angle between them is \(θ + 90^\circ\). The magnitude of \(δ\textbf{A}\) in spherical coordinates is \(a^2 \sin θδθδ \phi\), and the magnitude of \(\textbf{g}\) is (see Equation 5.4.15) \(\frac{2Gλ}{a \sin θ}.\) The dot product \(\textbf{g}⋅δ \textbf{A}\) is
\[ \frac{2Gλ}{a \sin θ} \cdot a^2 \sin θδθδ \phi \cdot \cos ( θ + 90^\circ) = - 2 G λ a \sin θδθδ \phi . \label{5.6.4} \tag{5.6.4}\]
To find the total flux, this must be integrated from \(\phi = 0\) to \(2 \pi \) and from \(θ = 0\) to \(\pi\). The result, as expected, is \(−8 \pi Gαλ\).


