5.7: Potential
- Page ID
- 8143
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)If work is required to move a mass from point \(\text{A}\) to point \(\text{B}\), there is said to be a gravitational potential difference between \(\text{A}\) and \(\text{B}\), with \(\text{B}\) being at the higher potential. The work required to move unit mass from \(\text{A}\) to \(\text{B}\) is called the potential difference between \(\text{A}\) and \(\text{B}\). In SI units it is expressed in \(\text{J kg}^{−1}\).
We have defined only the potential difference between two points. If we wish to define the potential at a point, it is necessary arbitrarily to define the potential at a particular point to be zero. We might, for example define the potential at floor level to be zero, in which case the potential at a height \(h\) above the floor is \(gh\); equally we may elect to define the potential at the level of the laboratory bench top to be zero, in which case the potential at a height \(z\) above the bench top is \(gz\). Because the value of the potential at a point depends on where we define the zero of potential, one often sees that the potential at some point is equal to some mathematical expression plus an arbitrary constant. The value of the constant will be determined once we have decided where we wish to define zero potential.
In celestial mechanics it is usual to assign zero potential to all points at an infinite distance from any bodies of interest.
Suppose we decide to define the potential at point \(\text{A}\) to be zero, and that the potential at \(\text{B}\) is then \(ψ\) \(\text{J kg}^{−1}\). If we move a point mass \(m\) from \(\text{A}\) to \(\text{B}\), we shall have to do an amount of work equal to \(mψ \ \text{J}\). The potential energy of the mass \(m\) when it is at \(\text{B}\) is then \(mψ\). In these notes, I shall usually use the symbol \(ψ\) for the potential at a point, and the symbol \(V\) for the potential energy of a mass at a point.
In moving a point mass from \(\text{A}\) to \(\text{B}\), it does not matter what route is taken. All that matters is the potential difference between \(\text{A}\) and \(\text{B}\). Forces that have the property that the work required to move from one point to another is route-independent are called conservative forces; gravitational forces are conservative. The potential at a point is a scalar quantity; it has no particular direction associated with it.
If it requires work to move a body from point \(\text{A}\) to point \(\text{B}\) (i.e. if there is a potential difference between \(\text{A}\) and \(\text{B}\), and \(\text{B}\) is at a higher potential than \(\text{A}\)), this implies that there must be a gravitational field directed from \(\text{B}\) to \(\text{A}\).
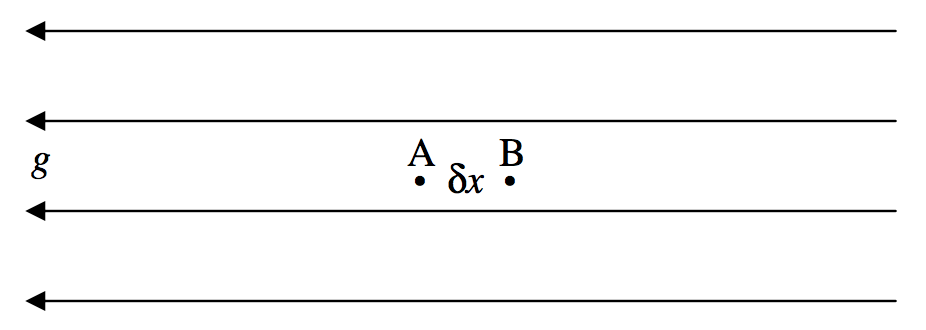
\(\text{FIGURE V.22}\)
Figure \(\text{V.22}\) shows two points, \(\text{A}\) and \(\text{B}\), a distance \(δx\) apart, in a region of space where the gravitational field is \(g\) directed in the negative \(x\) direction. We’ll suppose that the potential difference between \(\text{A}\) and \(\text{B}\) is \(δψ\). By definition, the work required to move unit mass from \(\text{A}\) to \(\text{B}\) is \(δψ\). Also by definition, the force on unit mass is \(g\), so that the work done on unit mass is \(gδx\). Thus we have
\[g = - \frac{dψ}{dx}. \label{5.7.1} \tag{5.7.1}\]
The minus sign indicates that, while the potential increases from left to right, the gravitational field is directed to the left. In words, the gravitational field is minus the potential gradient.
This was a one-dimensional example. In a later section, when we discuss the vector operator \(\nabla\), we shall write Equation \(\ref{5.7.1}\) in its three-dimensional form
\[\textbf{g} = - \textbf{grad}ψ = - \nabla ψ. \label{5.7.2} \tag{5.7.2}\]
While \(ψ\) itself is a scalar quantity, having no directional properties, its gradient is, of course, a vector.


