11.6: Curve of Growth for Voigt Profiles
Our next task is to construct curves of growth for Voigt profiles for different values of the ratio of the lorentzian and gaussian HWHMs, \(l/g\), which is
\[\tag{11.6.1}\label{11.6.1}\frac{l}{g}=\frac{\Gamma \lambda_0}{4\pi V_\text{m}\sqrt{\ln 2}}=\frac{\Gamma \lambda_0}{V_\text{m}\pi \sqrt{\ln 65536}}=\frac{\Gamma \lambda_0}{34.841V_\text{m}},\]
or, better, for different values of the gaussian ratio \(k_G =\frac{g}{l+g}\). These should look intermediate in appearance between figures XI.3 and 5.
The expression for the equivalent width in wavelength units is given by Equation 11.3.4:
\[\tag{11.3.4}\label{11.3.4}W=2\int_0^\infty \left [ 1-\text{exp}\left \{ -\tau(x)\right \}\right ]\,dx.\]
combined with Equation 10.5.20
\[\tag{10.5.20}\label{10.5.20}\tau (x) = Cl \tau (0)\int_{-\infty}^\infty \frac{\text{exp}\left [ -(ξ-x)^2\ln 2/g^2\right ]}{ξ^2+l^2}\,dξ.\]
That is:
\[\tag{11.6.2}\label{11.6.2}W=2\int_0^\infty \left ( 1-\text{exp} \left \{ -Cl\tau(0)\int_{-\infty}^\infty \frac{\text{exp}\left [ -(ξ-x)^2\ln 2/g^2 \right ]}{ξ^2+l^2}dξ\right \}\right )\,dx.\]
Here
- \(x = \lambda − \lambda_0\), \(l\) is the Lorentzian \(\text{HWHM} = \lambda_0^2\Gamma/(4\pi c)\) (where \(\Gamma\) may include a pressure-broadening contribution),
- \(g\) is the gaussian \(\text{HWHM} = V_\text{m}\lambda_0\sqrt{\ln 2} / c\) (where \(V_\text{m}\) may include a microturbulence contribution), and
- \(W\) is the equivalent width, all of dimension \(L\).
The symbol \(ξ\), also of dimension L, is a dummy variable, which disappears after the definite integration. \(\tau(0)\) is the optical thickness at the line centre. \(C\) is a dimensionless number given by Equation 10.5.23 and tabulated as a function of gaussian fraction in Chapter 10. The reader is urged to check the dimensions of Equation \ref{11.6.2} carefully. The integration of Equation \ref{11.6.2} is discussed in Appendix A.
Our aim is to calculate the equivalent width as a function of \(\tau(0)\) for different values of the gaussian fraction \(k_G = g/(l + g)\). What we find is as follows. Let \(W^\prime = W \sqrt{\ln 2 }/g\); that is, \(W^\prime\) is the equivalent width expressed in units of \(g /\sqrt{ \ln 2}\). For \(\tau(0)\) less than about 5, where the wings contribute relatively little to the equivalent width, we find that \(W^\prime\) is almost independent of the gaussian fraction. The difference in behaviour of the curve of growth for different profiles appears only for large values of \(\tau (0)\), when the wings assume a larger role. However, for any profile which is less gaussian than about \(k_G\) equal to about 0.9, the behaviour of the curve of growth (for \(\tau(0) > 5\)) mimics that for a lorentzian profile. For that reason I have drawn curves of growth in figure XI.6 only for \(k_G = 0.9, 0.99, 0.999\text{ and }1\). This corresponds to \(l/g = 0.1111, 0.0101, 0.0010\text{ and }0\), or to \(\Gamma \lambda_0 /V_m = 1.162, 0.1057, 0.0105\text{ and }0\) respectively.
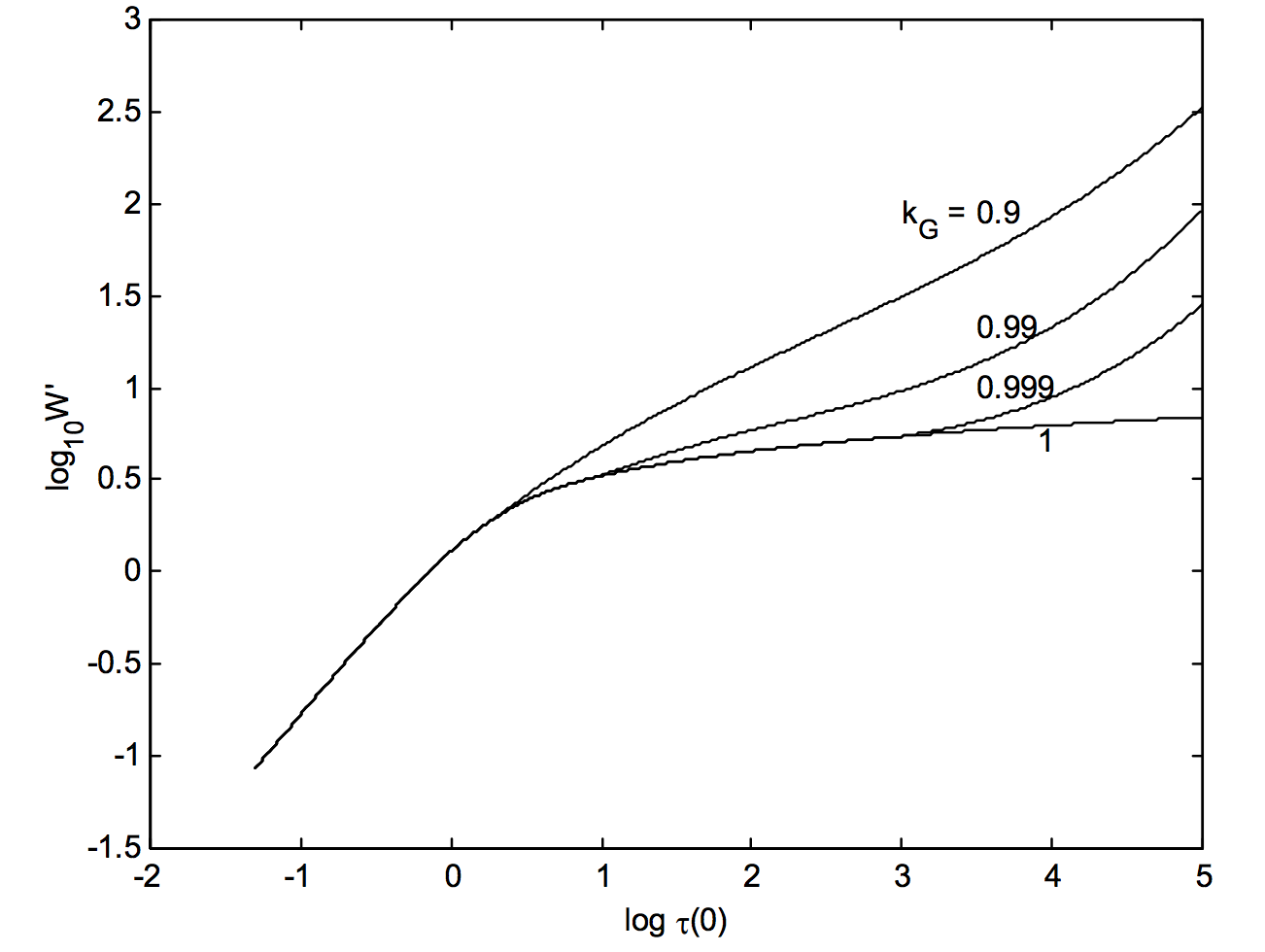
\(\text{FIGURE XI.6}\)