4.7: Electromotive Force and Internal Resistance
( \newcommand{\kernel}{\mathrm{null}\,}\)
The reader is reminded of the following definition from section 4.1:
Definition. The potential difference across the poles of a cell when no current is being taken from it is called the electromotive force (EMF) of the cell.
I shall use the symbol E for EMF.
Question. A 4 Ω resistance is connected across a cell of EMF 2 V. What current flows?
The immediate answer is 0.5 A – but this is likely to be wrong. The reason is that a cell has a resistance of its own – its internal resistance. The internal resistance of a lead-acid cell is typically quite small, but most dry cells have an appreciable internal resistance. If the external resistance is R and the internal resistance is r, the total resistance of the circuit is R+r, so that the current that flows is E/(R+r).
Whenever a current is taken from a cell (or battery) the potential difference across its poles drops to a value less than its EMF. We can think of a cell as an EMF in series with an internal resistance:
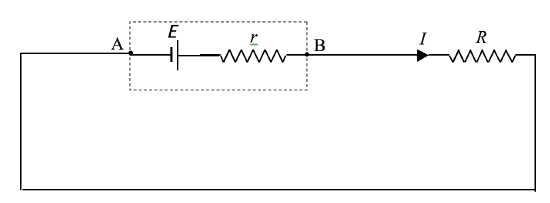
FIGURE IV.4
If we take the point A as having zero potential, we see that the potential of the point B will be E - Ir, and this, then, is the potential difference across the poles of the cell when a current I is being taken from it.


