17.9: Vibrating String

Last updated
Save as PDF

Page ID: 8503

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

It is possible that the three modes of vibration of the three masses in Section 17.8 reminded you of the fundamental and first two harmonic vibrations of a stretched string – and it is quite proper that it did. If you were to imagine ten masses attached to a stretched string and to carry out the same sort of analysis, you would find ten normal modes, of which one would be quite like the fundamental mode of a stretched string, and the remainder would remind you of the first nine harmonics. You could continue with the same analysis but with a very large number of masses, and eventually you would be analysing the vibrations of a continuous heavy string. We do that now, and we assume that we have a heavy, taut string of mass \( \mu \) per unit length, and under a tension \( F \).

alt

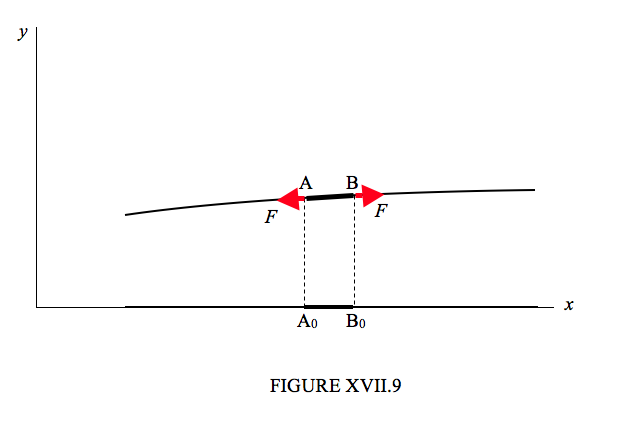
I show in Figure XVII.9 a portion of length \( \delta x \) of a vibrating rope, represented by \(A_0B_0\) in its equilibrium position and by AB in a displaced position. The rope makes an angle \(\psi \)A with the horizontal at A and an angle \(\psi\) B with the horizontal at B. The tension in the rope is \(F\). The vertical equation of motion is

\[ F(\sin \psi_B - \sin \psi_A ) = \mu\delta x\dfrac{\partial^2y}{\partial t^2} . \label{17.9.1} \]

If the angles are small, then \( \sin \psi \cong \frac{\partial y }{\partial x }\), so the expression in parenthesis is \( \frac{\partial ^2 y }{\partial x^2 }\delta x \). The equation of motion is therefore

\[ c^2 \dfrac{\partial ^2 y}{\partial x^2} = \frac{ \partial^2 y}{\partial t ^2} \label{17.9.2a} \]

where

\[c = \sqrt{\frac{T}{\mu}} \label{17.9.2b} \]

As can be verified by substitution, the general solution to this is of the form

\[ y = f (x-ct) + g(x + ct) \label{17.9.3} \]

This represents a function that can travel in either direction along the rope at a speed \( c\) given by Equation \(\ref{17.9.2b}\). Should the disturbance be a periodic disturbance, then a wave will travel along the rope at that speed. Further analysis of waves in ropes and strings is generally done in chapters concerned with wave motion. This section, however, at least establishes the speed at which a disturbance (periodic or otherwise) travels along a stretched strong or rope.