2.2: Meaning of Rotational Inertia
- Page ID
- 6933
If a force acts of a body, the body will accelerate. The ratio of the applied force to the resulting acceleration is the inertia (or mass) of the body.
If a torque acts on a body that can rotate freely about some axis, the body will undergo an angular acceleration. The ratio of the applied torque to the resulting angular acceleration is the rotational inertia of the body. It depends not only on the mass of the body, but also on how that mass is distributed with respect to the axis.
Consider the system shown in Figure II.1.
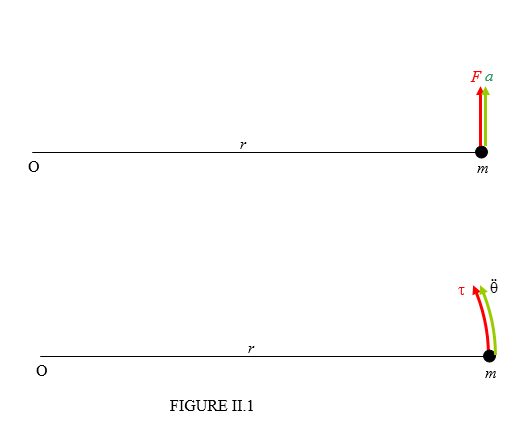
A particle of mass \( m \) is attached by a light (i.e. zero or negligible mass) arm of length \( r \) to a point at O, about which it can freely rotate. A force \( F \) is applied, and the mass consequently undergoes a linear acceleration \( a = \frac{F}{m} \). The angular acceleration is then \(\ddot{\Theta} = F.mr \). Also, the torque is \(\tau = Fr \) . The ratio of the applied torque to the angular acceleration is therefore \( mr^{2} \). Thus the rotational inertia is the second moment of inertia. Rotational inertia and (second) moment of inertia are one and the same thing, except that rotational inertia is a physical concept and moment of inertia is its mathematical representation.


