2.13: Momental Ellipse
- Page ID
- 8363
Consider a plane lamina such that its radius of gyration about some axis through the centre of mass is \(k\). Let P be a vector in the direction of that axis, originating at the centre of mass, given by
\[ {\bf P} = \frac{a^2}{k} {\bf\hat{r}} \label{eq:2.13.1} \]
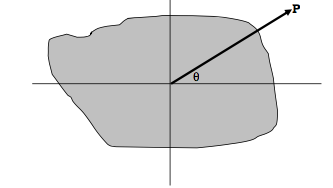
Here \( \bf \hat{r} \) is a unit vector in the direction of interest; \( k \) is the radius of gyration, and \( a \) is an arbitrary length introduced so that the dimensions of \( \bf P \) are those of length, and the length of the vector\( \bf P \) is inversely proportional to the radius of gyration. The moment of inertia is \(Mk^2 = \frac{Ma^4}{ P^2} \). That is to say
\[ \frac{Ma^4}{P^2} = A \cos ^2 \theta - 2 H \sin \theta \cos \theta + B \sin^2 \theta, \tag{2.13.2}\label{eq:2.13.2} \]
where \(A, H \) and \(B \) are the moments with respect to the \(x \)- and \(y \)-axes. Let \( (x , y)\) be the coordinates of the tip of the vector \( \bf P \), so that \(x = P\cos \theta \) and \(y = P\sin \theta \). Then
\[ Ma^4 = Ax^2 -2Hxy + By^2 .\label{eq:2.13.3} \]
Thus, no matter what the shape of the lamina, however irregular and asymmetric, the tip of the vector \( \bf P \) traces out an ellipse, whose axes are inclined at angles \( \frac{1}{2} \tan^{-1} (\frac{2H}{B-A} ) \) to the \(x \) - axis.
This is the momental ellipse, and the axes of the momental ellipse are the principal axes of the lamina.
Consider a regular \(n\)-gon. By symmetry the moment of inertia is the same about any two axes in the plane inclined at \( 2 \pi / n \) to each other. This is possible only if the momental ellipse is a circle. It follows that the moment of inertia of a uniform polygonal plane lamina is the same about any axis in its plane and passing through its centroid.
Show that the moment of inertia of a uniform plane \(n \) - gon of side \(2a \) about any axis in its plane and passing through its centroid is \( \frac{1}{12} ma^2 (1+3\cot^2 ( \pi /n)) \).
What is this for a square? For an equilateral triangle?


