20.2: Surface Tension
- Page ID
- 7059
The cause of surface tension is often explained roughly as follows. Molecules within a liquid are subject to intermolecular forces whose exact nature and origin need not concern us other than to say that they are principally van der Waals forces and they hold the liquid together and prevent it from evaporating. A molecule deep within the liquid is surrounded in all directions by other molecules, and so the net force on it averages zero. But a molecule on the surface experiences forces from beneath the surface, and consequently it tends to get dragged beneath the surface. This results in as few molecules as possible remaining on the surface; i.e. it results in the surface contracting to as small an area as possible consistent with whatever other geometrical constraints may exist. That is, the surface appears to be in a state of tension causing it to contract to the least possible area.
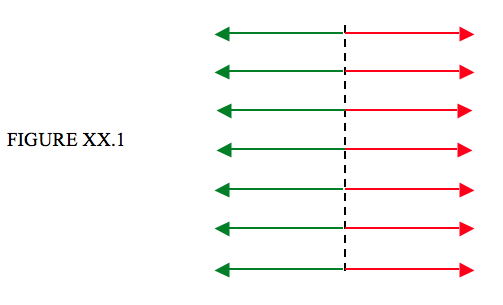
This tension can be described qualitatively thus. In Figure XX.1, the dashed line is an imaginary line drawn in the surface of a liquid. The liquid to the left of the line is being pulled to the right as indicated by the red arrows; the liquid to the right of the line is being pulled equally to the left as indicated by the green arrows. The force per unit length perpendicular to a line drawn in the surface of the liquid is the surface tension. Its SI unit is newtons per metre, and its CGS unit is dynes per centimetre. The dimensions are MT−2.
I have seen various symbols, such as \(T , S \) and \( \gamma \) used for surface tension. The first two of these symbols are already heavily worked in thermodynamics, so I shall use the symbol \( \gamma \) (although, it must be admitted, \( \gamma \) is heavily worked in thermodynamics, too.) Not everyone is comfortable with a definition involving forces perpendicular to an imaginary line drawn in the surface, and an alternative approach may be more palatable to some. The idea of a molecule beneath the surface being surrounded on all sides by other molecules and hence experiencing zero net average force, while a molecule on the surface is pulled asymmetrically by the molecules beneath it, remains. But instead of drawing an imaginary line on the surface, we reason that it requires work to move a molecule from within the liquid to the surface, and it requires a lot of work to move many molecules from beneath to the surface. That is, it requires work to create new surface. Thus we can define surface tension as the work required to create unit area of new surface. The conditions under which this work is done have to be carefully defined in any precise definition, and, from a thermodynamical point of view, the strict definition is the increase in the Gibbs free energy per unit area of new surface created under conditions of constant temperature and pressure. That is:
\[ \gamma = \left(\frac{\partial G}{\partial A}\right)_{T,P}\label{20.2.1}\tag{20.2.1} \]
This is consistent with the definition of the Gibbs free energy as a quantity whose increase is equal to the work , other than \(PdV\) work, done on a system in a reversible, isothermal isobaric process.
Such a nicety will be of interest to those versed in thermodynamics (and I have added a bit about the thermodynamics of surface energy in Chapter 12 of Thermodynamics), but for those not so versed, you may, without any serious prejudice to understanding most of the matter in this section, think of surface tension either as the force per unit length perpendicular to an imaginary line in the surface, or as the work required to create unit area of new surface. You may express surface tension either in newtons per metre or in joules per square metre (or, if you are of CGS persuasion, dynes per centimetre or ergs per square centimetre). These are dimensionally equivalent.metre or in joules per square metre (or, if you are of CGS persuasion, dynes per centimetre or ergs per square centimetre). These are dimensionally equivalent.


