4.2: Angular Velocity and Eulerian Angles
- Page ID
- 6947
Let \( Oxyz\) be a set of space-fixed axis, and let \( Ox_{0}y_{0}z_{0}\) be the body-fixed principal axes of a rigid body.
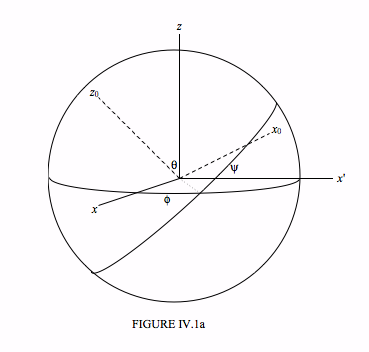
The orientation of the body-fixed principal axes \( Ox_{0}y_{0}z_{0}\) with respect to the space-fixed axes \( Oxyz\) can be described by the three Euler angles: \( \theta\), \(\phi\), and \(\psi\). These are illustrated in Figure IV.1a. Those who are not familiar with Euler angles or who would like a reminder can refer to their detailed description in Chapter 3 of my notes on Celestial Mechanics.
We are going to examine the motion of a body that is rotating about a non-principal axis. If the body is freely rotating in space with no external torques acting upon it, its angular momentum \( \bf{L}\) will be constant in magnitude and direction. The angular velocity vector \( \bf{\omega} \), however, will not be constant, but will wander with respect to both the space-fixed and body-fixed axes, and we shall be examining this motion. I am going to call the instantaneous components of \(\omega \) relative to the body-fixed axes \( \omega_{1} , \omega_{2}, \omega_{3} \), and its magnitude \(\omega\). As the body tumbles over and over, its Euler angles will be changing continuously. We are going to establish a geometrical relation between the instantaneous rates of change of the Euler angles and the instantaneous components of \( \omega\). That is, we are going to find how \( \omega_{1} , \omega_{2}\) and \( \omega_{3}\) are related to \( \dot{\theta} , \dot{\phi} \) and \( \dot{\psi}\).
I have indicated, in Figure VI.2a, the angular velocities \( \boldsymbol{\dot{\theta}} , \boldsymbol{\dot{\phi}} \) and \( \boldsymbol{\dot{\psi}}\) as vectors in what I hope will be agreed are the appropriate directions.
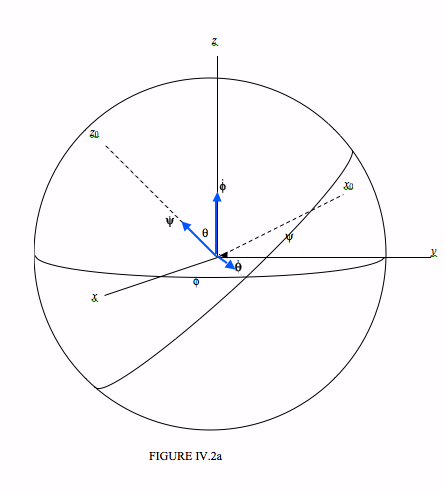
It should be clear that \(\omega_1\) is equal to the \( x_{0}\)-component of \( \boldsymbol{\dot{\phi}}\) plus the \( x_{0}\)-component of \( \boldsymbol{\dot{\theta}}\) and that \(\omega_2\) is equal to the \( y_{0}\)-component of \( \boldsymbol{\dot{\phi}}\) plus the \( y_{0}\)-component of \( \boldsymbol{\dot{\theta}}\) and that \(\omega_3\) is equal to the \( z_{0}\)-component of \( \boldsymbol{\dot{\phi}}\) plus \( \boldsymbol{\dot{\psi}}\)
Let us look at Figure IV.2b
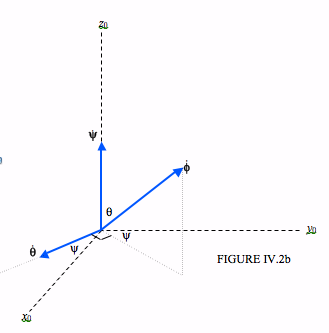
We see that the \( x_{0}\) and \( y_{0}\) components of \( \boldsymbol{\dot{\theta}}\) are \( \dot{\theta} \cos \psi \) and \( - \dot{\theta} \sin \psi \) respectively. The \( x_{0}\), \( y_{0}\) and \( z_{0}\) components of \( \boldsymbol{\dot{\phi}}\) are, respectively:
- \( \dot{\phi} \sin \theta \sin \psi\),
- \( \dot{\phi} \sin \theta \sin \psi\), and
- \( \dot{\phi} \cos \theta\).
Hence we arrive at
\[ \omega_{1} = \dot{\phi} \sin \theta \sin \psi + \dot{\theta} \cos \psi . \tag{4.2.1}\label{eq:4.2.1} \]
\[ \omega_{2} = \dot{\phi} \sin \theta \cos \psi - \dot{\theta} \sin \psi . \tag{4.2.2}\label{eq:4.2.2} \]
\[ \omega_{3} = \dot{\phi} \cos \theta + \dot{ \psi} \tag{4.2.3}\label{eq:4.2.3} \]


