5.3: Head-on Collision of a Moving Sphere with an Initially Stationary Sphere
- Page ID
- 6955
The coefficient of restitution is
\[ e = \dfrac{\text{relative speed of recession after collision}}{\text{relative speed of approach before collision}}. \tag{5.3.1}\label{eq:5.3.1} \]
We suppose that the two masses \( m_{1}\) and \( m_{2}\), the initial speed \( u\), and the coefficient of restitution \( e\) are known; we wish to find \( v_{1}\) and \( v_{2}\).
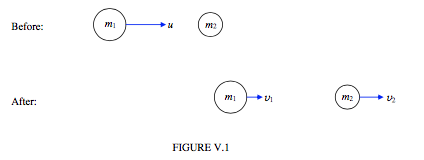
We evidently need two equations. Since there are no external forces on the system, the linear momentum of the system is conserved:
\[ m_{1}u = m_{1}v_{1} + m_{2}v_{2}. \tag{5.3.2}\label{eq:5.3.2} \]
The second equation will be the restitution equation (Equation \( \ref{eq:5.3.1}\)):
\[ v_{2}-v_{1} = eu. \tag{5.3.3}\label{eq:5.3.3} \]
These two equations can be solved to yield
\[ v_{1} = \left(\dfrac{m_{1}-m_{2}e}{m_{1}+m_{2}}\right)u \tag{5.3.4}\label{eq:5.3.4} \]
and
\[ v_{2} = \left(\dfrac{m_{1}(1+e)}{m_{1}+m_{2}}\right)u. \tag{5.3.5}\label{eq:5.3.5} \]The relation between the kinetic energy loss and the coefficient of restitution isn't quite as simple as in Section 5.2.
Show that
\[ \dfrac{\text{kinetic energy (after)}}{\text{kinetic energy (before)}} = \dfrac{m_{1}v_{1}^{2} +m_{1}v_{2}^{2} }{m_{1}u^{2}} = \dfrac{m_{1} + m_{2}e^{2}}{m_{1} + m_{2}}. \tag{5.3.6}\label{eq:5.3.6} \]
- If \( m_{2}=\infty\) (as in Section 5.2), this becomes just \( e^{2}\). If \( e = 1\), it becomes unity, so all is well.
- If \( m_{1}<<m_{2}\) (Ping-pong ball collides with cannon ball), \( v_{1}=-u,v_{2}=0\).
- If \( m_{1}=m_{2}\) (Ping-pong ball collides with ping-pong ball), \( v_{1}=0,v_{2}=u\).
- If \( m_{1}>>m_{2}\) (Cannon ball collides with ping-pong ball), \( v_{1}=u,v_{2}=2u\).
A moving sphere has a head-on elastic collision with an initially stationary sphere. After collision the kinetic energies of the two spheres are equal. Show that the mass ratio of the two spheres is 0.1716.
Which of the two spheres is the more massive? (I guarantee that your answer to this will be correct.)


