25.5: Dispersion - Rainbows and Prisms
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Explain the phenomenon of dispersion and discuss its advantages and disadvantages.
Everyone enjoys the spectacle of a rainbow glimmering against a dark stormy sky. How does sunlight falling on clear drops of rain get broken into the rainbow of colors we see? The same process causes white light to be broken into colors by a clear glass prism or a diamond. (See Figure 1.)

We see about six colors in a rainbow -- red, orange, yellow, green, blue, and violet; sometimes indigo is listed, too. Those colors are associated with different wavelengths of light, as shown in Figure 1. When our eye receives pure-wavelength light, we tend to see only one of the six colors, depending on wavelength. The thousands of other hues we can sense in other situations are our eye’s response to various mixtures of wavelengths. White light, in particular, is a fairly uniform mixture of all visible wavelengths. Sunlight, considered to be white, actually appears to be a bit yellow because of its mixture of wavelengths, but it does contain all visible wavelengths. The sequence of colors in rainbows is the same sequence as the colors plotted versus wavelength in Figure 2. What this implies is that white light is spread out according to wavelength in a rainbow. Dispersion is defined as the spreading of white light into its full spectrum of wavelengths. More technically, dispersion occurs whenever there is a process that changes the direction of light in a manner that depends on wavelength. Dispersion, as a general phenomenon, can occur for any type of wave and always involves wavelength-dependent processes.
DISPERSION
Dispersion is defined to be the spreading of white light into its full spectrum of wavelengths.
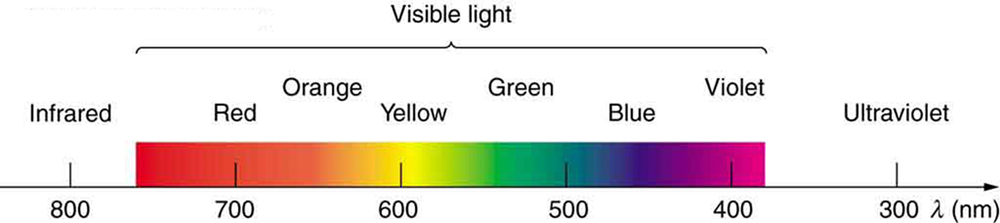
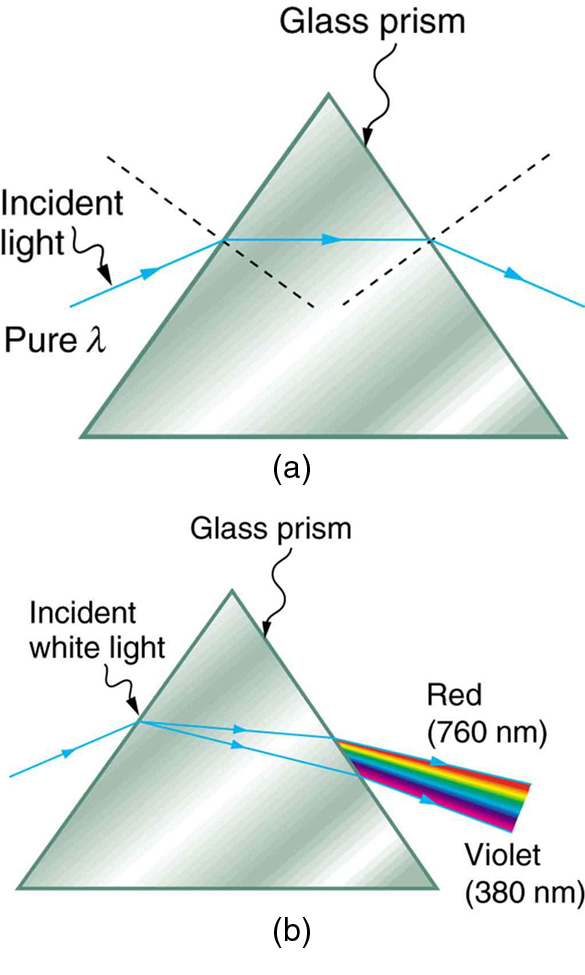
Refraction is responsible for dispersion in rainbows and many other situations. The angle of refraction depends on the index of refraction, as we saw in "The Law of Refraction." We know that the index of refraction n depends on the medium. But for a given medium, n also depends on wavelength (Table 25.5.1). Note that, for a given medium, n increases as wavelength decreases and is greatest for violet light. Thus violet light is bent more than red light, as shown for a prism in Figure 3 and the light is dispersed into the same sequence of wavelengths as seen in 1 and 2.
MAKING CONNECTIONS: DISPERSION
Any type of wave can exhibit dispersion. Sound waves, all types of electromagnetic waves, and water waves can be dispersed according to wavelength. Dispersion occurs whenever the speed of propagation depends on wavelength, thus separating and spreading out various wavelengths. Dispersion may require special circumstances and can result in spectacular displays such as in the production of a rainbow. This is also true for sound, since all frequencies ordinarily travel at the same speed. If you listen to sound through a long tube, such as a vacuum cleaner hose, you can easily hear it is dispersed by interaction with the tube. Dispersion, in fact, can reveal a great deal about what the wave has encountered that disperses its wavelengths. The dispersion of electromagnetic radiation from outer space, for example, has revealed much about what exists between the stars -- the so-called empty space.
| Medium | Red (660 nm) | Orange (610 nm) | Yellow (580 nm) | Green (550 nm) | Blue (470 nm) | Violet (410 nm) |
|---|---|---|---|---|---|---|
| Water | 1.331 | 1.332 | 1.333 | 1.335 | 1.338 | 1.342 |
| Diamond | 2.410 | 2.415 | 2.417 | 2.426 | 2.444 | 2.458 |
| Glass, crown | 1.512 | 1.514 | 1.518 | 1.519 | 1.524 | 1.530 |
| Glass, flint | 1.662 | 1.665 | 1.667 | 1.674 | 1.684 | 1.698 |
| Polustyrene | 1.488 | 1.490 | 1.492 | 1.493 | 1.499 | 1.506 |
| Quartz, fused | 1.455 | 1.456 | 1.458 | 1.459 | 1.462 | 1.468 |
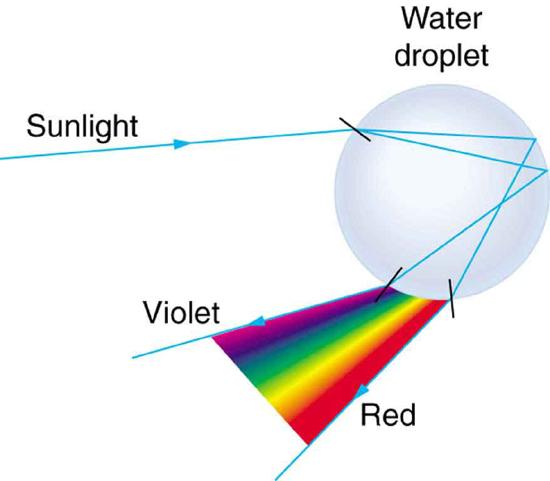
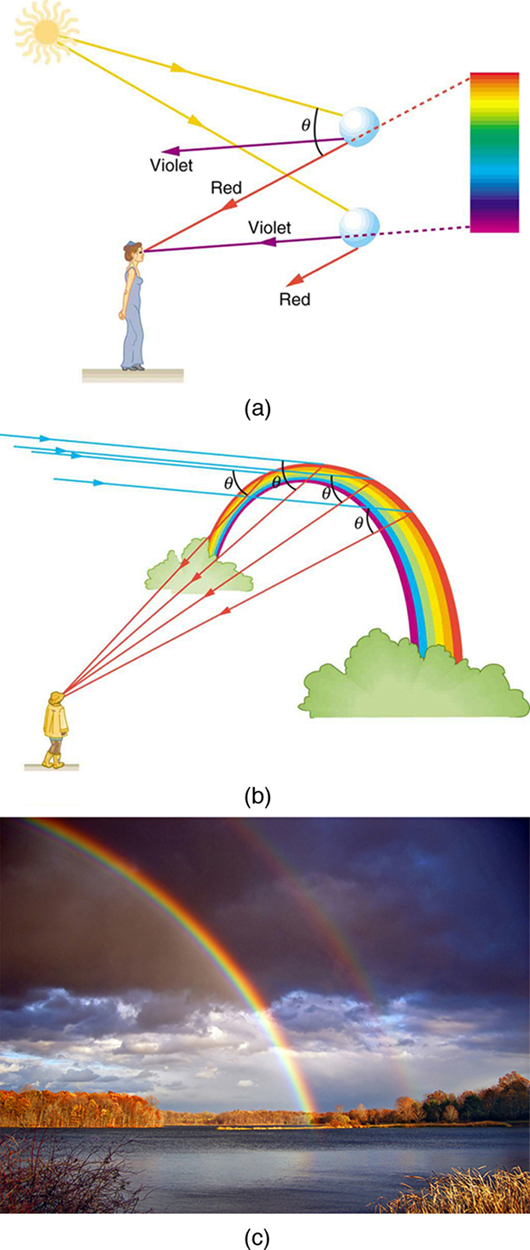
Rainbows are produced by a combination of refraction and reflection. You may have noticed that you see a rainbow only when you look away from the sun. Light enters a drop of water and is reflected from the back of the drop, as shown in Figure 4. The light is refracted both as it enters and as it leaves the drop. Since the index of refraction of water varies with wavelength, the light is dispersed, and a rainbow is observed, as shown in Figure 5a. (There is no dispersion caused by reflection at the back surface, since the law of reflection does not depend on wavelength.) The actual rainbow of colors seen by an observer depends on the myriad of rays being refracted and reflected toward the observer’s eyes from numerous drops of water. The effect is most spectacular when the background is dark, as in stormy weather, but can also be observed in waterfalls and lawn sprinklers. The arc of a rainbow comes from the need to be looking at a specific angle relative to the direction of the sun, as illustrated in Figure 5b. (If there are two reflections of light within the water drop, another “secondary” rainbow is produced. This rare event produces an arc that lies above the primary rainbow arc -- see Figure 5c.)
RAINBOWS
Rainbows are produced by a combination of refraction and reflection.
Dispersion may produce beautiful rainbows, but it can cause problems in optical systems. White light used to transmit messages in a fiber is dispersed, spreading out in time and eventually overlapping with other messages. Since a laser produces a nearly pure wavelength, its light experiences little dispersion, an advantage over white light for transmission of information. In contrast, dispersion of electromagnetic waves coming to us from outer space can be used to determine the amount of matter they pass through. As with many phenomena, dispersion can be useful or a nuisance, depending on the situation and our human goals.
PHET EXPLORATIONS: GEOMETRIC OPTICS
How does a lens form an image? See how light rays are refracted by a lens. Watch how the image changes when you adjust the focal length of the lens, move the object, move the lens, or move the screen.
Summary
- The spreading of white light into its full spectrum of wavelengths is called dispersion.
- Rainbows are produced by a combination of refraction and reflection and involve the dispersion of sunlight into a continuous distribution of colors.
- Dispersion produces beautiful rainbows but also causes problems in certain optical systems.
Glossary
- dispersion
- spreading of white light into its full spectrum of wavelengths
- rainbow
- dispersion of sunlight into a continuous distribution of colors according to wavelength, produced by the refraction and reflection of sunlight by water droplets in the sky


