12.E: Electromagnetism (Exercises)
- Page ID
- 1013
1. A particle with a charge of 1.0 C and a mass of 1.0 kg is observed moving past point P with a velocity \((1.0\ \text{m}/\text{s})\hat{\mathbf{x}}\). The electric field at point P is \((1.0\ \text{V}/\text{m})\hat{\mathbf{y}}\), and the magnetic field is \((2.0\ \text{T})\hat{\mathbf{y}}\). Find the force experienced by the particle.(answer check available at lightandmatter.com)
2. For a positively charged particle moving through a magnetic field, the directions of the \(\mathbf{v}\), \(\mathbf{B}\), and \(\mathbf{F}\) vectors are related by a right-hand rule:
Make a three-dimensional model of the three vectors using pencils or rolled-up pieces of paper to represent the vectors assembled with their tails together. Make all three vectors perpendicular to each other. Now write down every possible way in which the rule could be rewritten by scrambling up the three symbols \(\mathbf{v}\), \(\mathbf{B}\), and \(\mathbf{F}\). Referring to your model, which are correct and which are incorrect?
3. A charged particle is released from rest. We see it start to move, and as it gets going, we notice that its path starts to curve. Can we tell whether this region of space has \(\mathbf{E}\neq 0\), or \(\mathbf{B}\neq 0\), or both? Assume that no other forces are present besides the possible electrical and magnetic ones, and that the fields, if they are present, are uniform.
4. A charged particle is in a region of space in which there is a uniform magnetic field \(\mathbf{B}=B\hat{\mathbf{z}}\). There is no electric field, and no other forces act on the particle. In each case, describe the future motion of the particle, given its initial velocity.
- \(\mathbf{v}_\text{o}=0\)
- \(\mathbf{v}_\text{o}=(1\ \text{m}/\text{s})\hat{\mathbf{z}}\)
- \(\mathbf{v}_\text{o}=(1\ \text{m}/\text{s})\hat{\mathbf{y}}\)
5. (a) A line charge, with charge per unit length \(\lambda\), moves at velocity \(v\) along its own length. How much charge passes a given point in time \(dt\)? What is the resulting current? \hwans{hwans:linechargecurrent}
(b) Show that the units of your answer in part a work out correctly.
6. Two parallel wires of length \(L\) carry currents \(I_1\) and \(I_2\). They are separated by a distance \(R\), and we assume \(R\) is much less than \(L\), so that our results for long, straight wires are accurate. The goal of this problem is to compute the magnetic forces acting between the wires.
(a) Neither wire can make a force on itself. Therefore, our first step in computing wire 1's force on wire 2 is to find the magnetic field made only by wire 1, in the space occupied by wire 2. Express this field in terms of the given quantities.(answer check available at lightandmatter.com)
(b) Let's model the current in wire 2 by pretending that there is a line charge inside it, possessing density per unit length \(\lambda_2\) and moving at velocity \(v_2\). Relate \(\lambda_2\) and \(v_2\) to the current \(I_2\), using the result of problem 5a. Now find the magnetic force wire 1 makes on wire 2, in terms of \(I_1\), \(I_2\), \(L\), and \(R\). \hwans{hwans:forcebetweentwowires}
(c) Show that the units of the answer to part b work out to be newtons.
7. Suppose a charged particle is moving through a region of space in which there is an electric field perpendicular to its velocity vector, and also a magnetic field perpendicular to both the particle's velocity vector and the electric field. Show that there will be one particular velocity at which the particle can be moving that results in a total force of zero on it. Relate this velocity to the magnitudes of the electric and magnetic fields. (Such an arrangement, called a velocity filter, is one way of determining the speed of an unknown particle.)
8. The following data give the results of two experiments in which charged particles were released from the same point in space, and the forces on them were measured:
| q1 = 1 µC | \(\mathbf{v}_1=(1 m/s)\mathbf{\hat x}\) | \(\mathbf{F}_1=(-1 mN)\mathbf{\hat y}\) |
| q2 = - 2 µC | \(\mathbf{v}_2=(-1 m/s)\mathbf{\hat x}\) | \(\mathbf{F}_2=(-2 mN)\mathbf{\hat y}\) |
The data are insufficient to determine the magnetic field vector; demonstrate this by giving two different magnetic field vectors, both of which are consistent with the data.
9. The following data give the results of two experiments in which charged particles were released from the same point in space, and the forces on them were measured:
| q1 = 1 nC | \(\mathbf{v}_1=(1 m/s)\mathbf{\hat z}\) | \(\mathbf{F}_1=(5 mN)\mathbf{\hat x}+(2 mN)\mathbf{\hat y}\) |
| q2 = 1 nC | \(\mathbf{v}_2=(3 m/s)\mathbf{\hat z}\) | \(\mathbf{F}_2=(10 mN)\mathbf{\hat x}+(4 mN)\mathbf{\hat y}\) |
Is there a nonzero electric field at this point? A nonzero magnetic field?
10. This problem is a continuation of problem 6. Note that the answer to problem 6b is given on page 930.
- Interchanging the 1's and 2's in the answer to problem 6b, what is the magnitude of the magnetic force from wire 2 acting on wire 1? Is this consistent with Newton's third law?
- Suppose the currents are in the same direction. Make a sketch, and use the right-hand rule to determine whether wire 1 pulls wire 2 towards it, or pushes it away.
- Apply the right-hand rule again to find the direction of wire 2's force on wire 1. Does this agree with Newton's third law?
- What would happen if wire 1's current was in the opposite direction compared to wire 2's?
11. (a) In the photo of the vacuum tube apparatus in figure o on page 656, infer the direction of the magnetic field from the motion of the electron beam. (The answer is given in the answer to the self-check on that page.)
(b) Based on your answer to part a, find the direction of the currents in the coils.
(c) What direction are the electrons in the coils going?
(d) Are the currents in the coils repelling the currents consisting of the beam inside the tube, or attracting them? Check your answer by comparing with the result of problem 10.
12. A charged particle of mass \(m\) and charge \(q\) moves in a circle due to a uniform magnetic field of magnitude \(B\), which points perpendicular to the plane of the circle.
- Assume the particle is positively charged. Make a sketch showing the direction of motion and the direction of the field, and show that the resulting force is in the right direction to produce circular motion.
- Find the radius, \(r\), of the circle, in terms of \(m\), \(q\), \(v\), and \(B\).(answer check available at lightandmatter.com)
- Show that your result from part b has the right units.
- Discuss all four variables occurring on the right-hand side of your answer from part b. Do they make sense? For instance, what should happen to the radius when the magnetic field is made stronger? Does your equation behave this way?
- Restate your result so that it gives the particle's angular frequency, \(\omega\), in terms of the other variables, and show that \(v\) drops out.(answer check available at lightandmatter.com)
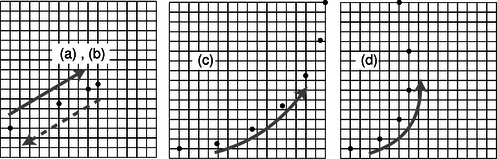
a / Problem 13.
13. Each figure represents the motion of a positively charged particle. The dots give the particles' positions at equal time intervals. In each case, determine whether the motion was caused by an electric force, a magnetic force, or a frictional force, and explain your reasoning. If possible, determine the direction of the magnetic or electric field. All fields are uniform. In (a), the particle stops for an instant at the upper right, but then comes back down and to the left, retracing the same dots. In (b), it stops on the upper right and stays there.
14. One model of the hydrogen atom has the electron circling around the proton at a speed of \(2.2\times10^6\) m/s, in an orbit with a radius of 0.05 nm. (Although the electron and proton really orbit around their common center of mass, the center of mass is very close to the proton, since it is 2000 times more massive. For this problem, assume the proton is stationary.)
- Treat the circling electron as a current loop, and calculate the current.
- Estimate the magnetic field created at the center of the atom by the electron.(answer check available at lightandmatter.com)
- Does the proton experience a nonzero force from the electron's magnetic field? Explain.
- Does the electron experience a magnetic field from the proton? Explain.
- Does the electron experience a magnetic field created by its own current? Explain.
- Is there an electric force acting between the proton and electron? If so, calculate it.(answer check available at lightandmatter.com)
- Is there a gravitational force acting between the proton and electron? If so, calculate it.
- An inward force is required to keep the electron in its orbit -- otherwise it would obey Newton's first law and go straight, leaving the atom. Based on your answers to the previous parts, which force or forces (electric, magnetic and gravitational) contributes significantly to this inward force? (Based on a problem by Arnold Arons.)
15. The equation \(B_z=\beta kIA/c^2r^3\) was found on page 666 for the distant field of a dipole. Show, as asserted there, that the constant \(\beta\) must be unitless.
16. The following data give the results of three experiments in which charged particles were released from the same point in space, and the forces on them were measured:
| q1 = 1 C | \(\mathbf{v}_1=0\) | \(\mathbf{F}_1=(1 N)\mathbf{\hat y}\) |
| q2 =1 C | \(\mathbf{v}_2=(1 m/s)\mathbf{\hat x}\) | \(\mathbf{F}_2=(1 N)\mathbf{\hat y}\) |
| q3 =1 C | \(\mathbf{v}_3=(1 m/s)\mathbf{\hat z}\) | \(\mathbf{F}_3=0\) |
Determine the electric and magnetic fields.(answer check available at lightandmatter.com)
17. If you put four times more current through a solenoid, how many times more energy is stored in its magnetic field?(answer check available at lightandmatter.com)
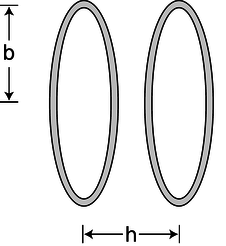
b / Problem 18.
18. A Helmholtz coil is defined as a pair of identical circular coils lying in parallel planes and separated by a distance, \(h\), equal to their radius, \(b\). (Each coil may have more than one turn of wire.) Current circulates in the same direction in each coil, so the fields tend to reinforce each other in the interior region. This configuration has the advantage of being fairly open, so that other apparatus can be easily placed inside and subjected to the field while remaining visible from the outside. The choice of \(h=b\) results in the most uniform possible field near the center. A photograph of a Helmholtz coil was shown in figure o on page 656.
(a) Find the percentage drop in the field at the center of one coil, compared to the full strength at the center of the whole apparatus. (answer check available at lightandmatter.com)
(b) What value of \(h\) (not equal to \(b)\) would make this percentage difference equal to zero?(answer check available at lightandmatter.com)
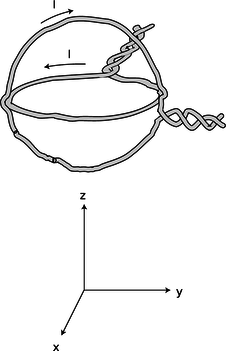
c / Problem 19.
19. The figure shows a nested pair of circular wire loops used to create magnetic fields. (The twisting of the leads is a practical trick for reducing the magnetic fields they contribute, so the fields are very nearly what we would expect for an ideal circular current loop.) The coordinate system below is to make it easier to discuss directions in space. One loop is in the \(y-z\) plane, the other in the \(x-y\) plane. Each of the loops has a radius of 1.0 cm, and carries 1.0 A in the direction indicated by the arrow.
- Calculate the magnetic field that would be produced by one such loop, at its center. (answer check available at lightandmatter.com)
- Describe the direction of the magnetic field that would be produced, at its center, by the loop in the \(x-y\) plane alone.
- Do the same for the other loop.
- Calculate the magnitude of the magnetic field produced by the two loops in combination, at their common center. Describe its direction.(answer check available at lightandmatter.com)

d / Problem 20.
20. Four long wires are arranged, as shown, so that their cross-section forms a square, with connections at the ends so that current flows through all four before exiting. Note that the current is to the right in the two back wires, but to the left in the front wires. If the dimensions of the cross-sectional square (height and front-to-back) are \(b\), find the magnetic field (magnitude and direction) along the long central axis.(answer check available at lightandmatter.com)
21. In problem 16, the three experiments gave enough information to determine both fields. Is it possible to design a procedure so that, using only two such experiments, we can always find \(\mathbf{E}\) and \(\mathbf{B}\)? If so, design it. If not, why not?
22. Use the Biot-Savart law to derive the magnetic field of a long, straight wire, and show that this reproduces the result of example 6 on page 658.
23. (a) Modify the calculation on page 663 to determine the component of the magnetic field of a sheet of charge that is perpendicular to the sheet.(answer check available at lightandmatter.com)
(b) Show that your answer has the right units.
(c) Show that your answer approaches zero as \(z\) approaches infinity.
(d) What happens to your answer in the case of \(a=b\)? Explain why this makes sense.
24. Consider two solenoids, one of which is smaller so that it can be put inside the other. Assume they are long enough so that each one only contributes significantly to the field inside itself, and the interior fields are nearly uniform. Consider the configuration where the small one is inside the big one with their currents circulating in the same direction, and a second configuration in which the currents circulate in opposite directions. Compare the energies of these configurations with the energy when the solenoids are far apart. Based on this reasoning, which configuration is stable, and in which configuration will the little solenoid tend to get twisted around or spit out? \hwhint{hwhint:nestedsolenoids}
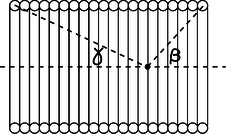
e / Problem 25.
25. (a) A solenoid can be imagined as a series of circular current loops that are spaced along their common axis. Integrate the result of example 12 on page 671 to show that the field on the axis of a solenoid can be written as \(B=(2\pi k\eta/c^2)(\cos\beta+\cos\gamma)\), where the angles \(\beta\) and \(\gamma\) are defined in the figure.
(b) Show that in the limit where the solenoid is very long, this exact result agrees with the approximate one derived in example 13 on page 674 using Ampère's law.
(c) Note that, unlike the calculation using Ampère's law, this one is valid at points that are near the mouths of the solenoid, or even outside it entirely. If the solenoid is long, at what point on the axis is the field equal to one half of its value at the center of the solenoid?
(d) What happens to your result when you apply it to points that are very far away from the solenoid? Does this make sense?
26. The first step in the proof of Ampère's law on page 675 is to show that Ampère's law holds in the case shown in figure f/1, where a circular Ampèrian loop is centered on a long, straight wire that is perpendicular to the plane of the loop. Carry out this calculation, using the result for the field of a wire that was established without using Ampère's law.
27. A certain region of space has a magnetic field given by \(\mathbf{B}=bx\hat{\mathbf{y}}\). Find the electric current flowing through the square defined by \(z=0\), \(0\le x \le a\), and \(0\le y \le a\).(answer check available at lightandmatter.com)

f / A nautilus shell is approximately a logarithmic spiral, of the type in problem 28.
28. Perform a calculation similar to the one in problem 54, but for a logarithmic spiral, defined by \(r=we^{u\theta}\), and show that the field is \(B=(kI/c^2u)(1/a-1/b)\). Note that the solution to problem 54 is given in the back of the book.
29. (a) For the geometry described in example 8 on page 661, find the field at a point the lies in the plane of the wires, but not between the wires, at a distance \(b\) from the center line. Use the same technique as in that example.
(b) Now redo the calculation using the technique demonstrated on page 666. The integrals are nearly the same, but now the reasoning is reversed: you already know \(\beta=1\), and you want to find an unknown field. The only difference in the integrals is that you are tiling a different region of the plane in order to mock up the currents in the two wires. Note that you can't tile a region that contains a point of interest, since the technique uses the field of a distant dipole.(answer check available at lightandmatter.com)
30. (a) A long, skinny solenoid consists of \(N\) turns of wire wrapped uniformly around a hollow cylinder of length \(\ell\) and cross-sectional area \(A\). Find its inductance.(answer check available at lightandmatter.com)
(b) Show that your answer has the right units to be an inductance.
31. Consider two solenoids, one of which is smaller so that it can be put inside the other. Assume they are long enough to act like ideal solenoids, so that each one only contributes significantly to the field inside itself, and the interior fields are nearly uniform. Consider the configuration where the small one is partly inside and partly hanging out of the big one, with their currents circulating in the same direction. Their axes are constrained to coincide.
(a) Find the difference in the magnetic energy between the configuration where the solenoids are separate and the configuration where the small one is inserted into the big one. Your equation will include the length \(x\) of the part of the small solenoid that is inside the big one, as well as other relevant variables describing the two solenoids.(answer check available at lightandmatter.com)
(b) Based on your answer to part a, find the force acting between the solenoids.(answer check available at lightandmatter.com)
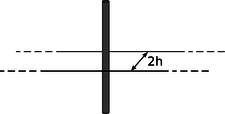
g / Problem 32.
32. Verify Ampère's law in the case shown in the figure, assuming the known equation for the field of a wire. A wire carrying current \(I\) passes perpendicularly through the center of the rectangular Ampèrian surface. The length of the rectangle is infinite, so it's not necessary to compute the contributions of the ends.
33. The purpose of this problem is to find how the gain of a transformer depends on its construction.
(a) The number of loops of wire, \(N\), in a solenoid is changed, while keeping the length constant. How does the impedance depend on \(N\)? State your answer as a proportionality, e.g., \(Z\propto N^3\) or \(Z\propto N^{-5}\).
(b) For a given AC voltage applied across the inductor, how does the magnetic field depend on \(N\)? You need to take into account both the dependence of a solenoid's field on \(N\) for a given current and your answer to part a, which affects the current.
(c) Now consider a transformer consisting of two solenoids. The input side has \(N_1\) loops, and the output \(N_2\). We wish to find how the output voltage \(V_2\) depends on \(N_1\), \(N_2\), and the input voltage \(V_1\). The text has already established \(V_2\propto V_1N_2\), so it only remains to find the dependence on \(N_1\). Use your result from part b to accomplish this. The ratio \(V_2/V_1\) is called the voltage gain.
34. Problem 33 dealt with the dependence of a transformer's gain on the number of loops of wire in the input solenoid. Carry out a similar analysis of how the gain depends on the frequency at which the circuit is operated.
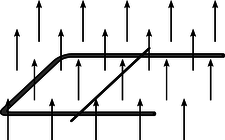
h / Problem 35.
35. A U-shaped wire makes electrical contact with a second, straight wire, which rolls along it to the right, as shown in the figure. The whole thing is immersed in a uniform magnetic field, which is perpendicular to the plane of the circuit. The resistance of the rolling wire is much greater than that of the U.
(a) Find the direction of the force on the wire based on conservation of energy.
(b) Verify the direction of the force using right-hand rules.
(c) Find magnitude of the force acting on the wire. There is more than one way to do this, but please do it using Faraday's law (which works even though it's the Ampèrian surface itself that is changing, rather than the field).(answer check available at lightandmatter.com)
(d) Consider how the answer to part a would have changed if the direction of the field had been reversed, and also do the case where the direction of the rolling wire's motion is reversed. Verify that this is in agreement with your answer to part c.
36. A charged particle is in motion at speed \(v\), in a region of vacuum through which an electromagnetic wave is passing. In what direction should the particle be moving in order to minimize the total force acting on it? Consider both possibilities for the sign of the charge. (Based on a problem by David J. Raymond.)
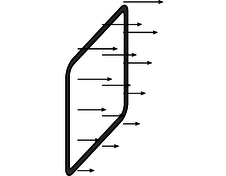
i / Problem 37.
37. A wire loop of resistance \(R\) and area \(A\), lying in the \(y-z\) plane, falls through a nonuniform magnetic field \(\mathbf{B}=kz\hat{\mathbf{x}}\), where \(k\) is a constant. The \(z\) axis is vertical.
(a) Find the direction of the force on the wire based on conservation of energy.
(b) Verify the direction of the force using right-hand rules.
(c) Find the magnetic force on the wire.(answer check available at lightandmatter.com)
38. A capacitor has parallel plates of area \(A\), separated by a distance \(h\). If there is a vacuum between the plates, then Gauss's law gives \(E=4\pi k\sigma=4\pi kq/A\) for the field between the plates, and combining this with \(E=V/h\), we find \(C=q/V=(1/4\pi k)A/h\). (a) Generalize this derivation to the case where there is a dielectric between the plates. (b) Suppose we have a list of possible materials we could choose as dielectrics, and we wish to construct a capacitor that will have the highest possible energy density, \(U_e/v\), where \(v\) is the volume. For each dielectric, we know its permittivity \(\epsilon\), and also the maximum electric field \(E\) it can sustain without breaking down and allowing sparks to cross between the plates. Write the maximum energy density in terms of these two variables, and determine a figure of merit that could be used to decide which material would be the best choice.
39. (a) For each term appearing on the right side of Maxwell's equations, give an example of an everyday situation it describes.
(b) Most people doing calculations in the SI system of units don't use \(k\) and \(k/c^2\). Instead, they express everything in terms of the constants
Rewrite Maxwell's equations in terms of these constants, eliminating \(k\) and \(c\) everywhere.
40. (a) Prove that in an electromagnetic plane wave, half the energy is in the electric field and half in the magnetic field.
(b) Based on your result from part a, find the proportionality constant in the relation \(d\mathbf{p}\propto\mathbf{E}\times\mathbf{B}dv\), where \(d \mathbf{p}\) is the momentum of the part of a plane light wave contained in the volume \(dv\). The vector \(\mathbf{E}\times\mathbf{B}\) is known as the Poynting vector. (To do this problem, you need to know the relativistic relationship between the energy and momentum of a beam of light.)(answer check available at lightandmatter.com)
41. (a) A beam of light has cross-sectional area \(A\) and power \(P\), i.e., \(P\) is the number of joules per second that enter a window through which the beam passes. Find the energy density \(U/v\) in terms of \(P\), \(A\), and universal constants.
(b) Find \(\tilde{\mathbf{E}}\) and \(\tilde{\mathbf{B}}\), the amplitudes of the electric and magnetic fields, in terms of \(P\), \(A\), and universal constants (i.e., your answer should not include \(U\) or \(v\)). You will need the result of problem 40a. A real beam of light usually consists of many short wavetrains, not one big sine wave, but don't worry about that.(answer check available at lightandmatter.com)\hwhint{hwhint:solarconstant}
(c) A beam of sunlight has an intensity of \(P/A=1.35\times10^3\ \text{W}/\text{m}^2\), assuming no clouds or atmospheric absorption. This is known as the solar constant. Compute \(\tilde{\mathbf{E}}\) and \(\tilde{\mathbf{B}}\), and compare with the strengths of static fields you experience in everyday life: \(E \sim 10^6\ \text{V}/\text{m}\) in a thunderstorm, and \(B \sim 10^{-3}\) T for the Earth's magnetic field.(answer check available at lightandmatter.com)
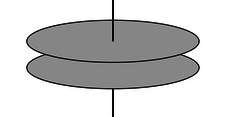
j / Problem 42.
42. The circular parallel-plate capacitor shown in the figure is being charged up over time, with the voltage difference across the plates varying as \(V=st\), where \(s\) is a constant. The plates have radius \(b\), and the distance between them is \(d\). We assume \(d \ll b\), so that the electric field between the plates is uniform, and parallel to the axis. Find the induced magnetic field at a point between the plates, at a distance \(R\) from the axis. \hwhint{hwhint:circularcap}(answer check available at lightandmatter.com)
43. A positively charged particle is released from rest at the origin at \(t=0\), in a region of vacuum through which an electromagnetic wave is passing. The particle accelerates in response to the wave. In this region of space, the wave varies as \(\mathbf{E}=\hat{\mathbf{x}}\tilde{E}\sin\omega t\), \(\mathbf{B}=\hat{\mathbf{y}}\tilde{B}\sin\omega t\), and we assume that the particle has a relatively large value of \(m/q\), so that its response to the wave is sluggish, and it never ends up moving at any speed comparable to the speed of light. Therefore we don't have to worry about the spatial variation of the wave; we can just imagine that these are uniform fields imposed by some external mechanism on this region of space.
(a) Find the particle's coordinates as functions of time.(answer check available at lightandmatter.com)
(b) Show that the motion is confined to \(-z_{max}\leq z \leq z_{max}\), where \(z_{max} = 1.101\left(q^2\tilde{E}\tilde{B}/m^2\omega^3\right)\).
44. Electromagnetic waves are supposed to have their electric and magnetic fields perpendicular to each other. (Throughout this problem, assume we're talking about waves traveling through a vacuum, and that there is only a single sine wave traveling in a single direction, not a superposition of sine waves passing through each other.) Suppose someone claims they can make an electromagnetic wave in which the electric and magnetic fields lie in the same plane. Prove that this is impossible based on Maxwell's equations.
45. Repeat the self-check on page 710, but with one change in the procedure: after we charge the capacitor, we open the circuit, and then continue with the observations.
46. On page 713, I proved that \(\mathbf{H}_{\parallel,1}=\mathbf{H}_{\parallel,2}\) at the boundary between two substances if there is no free current and the fields are static. In fact, each of Maxwell's four equations implies a constraint with a similar structure. Some are constraints on the field components parallel to the boundary, while others are constraints on the perpendicular parts. Since some of the fields referred to in Maxwell's equations are the electric and magnetic fields \(\mathbf{E}\) and \(\mathbf{B}\), while others are the auxiliary fields \(\mathbf{D}\) and \(\mathbf{H}\), some of the constraints deal with \(\mathbf{E}\) and \(\mathbf{B}\), others with \(\mathbf{D}\) and \(\mathbf{H}\). Find the other three constraints.
47. (a) Figure j on page 714 shows a hollow sphere with \(\mu/\mu_\text{o}=x\), inner radius \(a\), and outer radius \(b\), which has been subjected to an external field \(\mathbf{B}_\text{o}\). Finding the fields on the exterior, in the shell, and on the interior requires finding a set of fields that satisfies five boundary conditions: (1) far from the sphere, the field must approach the constant \(\mathbf{B}_\text{o}\); (2) at the outer surface of the sphere, the field must have \(\mathbf{H}_{\parallel,1}=\mathbf{H}_{\parallel,2}\), as discussed on page 713; (3) the same constraint applies at the inner surface of the sphere; (4) and (5) there is an additional constraint on the fields at the inner and outer surfaces, as found in problem 46. The goal of this problem is to find the solution for the fields, and from it, to prove that the interior field is uniform, and given by
This is a very difficult problem to solve from first principles, because it's not obvious what form the fields should have, and if you hadn't been told, you probably wouldn't have guessed that the interior field would be uniform. We could, however, guess that once the sphere becomes polarized by the external field, it would become a dipole, and at \(r\gg b\), the field would be a uniform field superimposed on the field of a dipole. It turns out that even close to the sphere, the solution has exactly this form. In order to complete the solution, we need to find the field in the shell (\(a\lt r\lt b\)), but the only way this field could match up with the detailed angular variation of the interior and exterior fields would be if it was also a superposition of a uniform field with a dipole field. The final result is that we have four unknowns: the strength of the dipole component of the external field, the strength of the uniform and dipole components of the field within the shell, and the strength of the uniform interior field. These four unknowns are to be determined by imposing constraints (2) through (5) above.
(b) Show that the expression from part a has physically reasonable behavior in its dependence on \(x\) and \(a/b\).
48. Two long, parallel strips of thin metal foil form a configuration like a long, narrow sandwich. The air gap between them has height \(h\), the width of each strip is \(w\), and their length is \(\ell\). Each strip carries current \(I\), and we assume for concreteness that the currents are in opposite directions, so that the magnetic force, \(F\), between the strips is repulsive.
(a) Find the force in the limit of \(w\gg h\).(answer check available at lightandmatter.com)
(b) Find the force in the limit of \(w\ll h\), which is like two ordinary wires.
(c) Discuss the relationship between the two results.
49. Suppose we are given a permanent magnet with a complicated, asymmetric shape. Describe how a series of measurements with a magnetic compass could be used to determine the strength and direction of its magnetic field at some point of interest. Assume that you are only able to see the direction to which the compass needle settles; you cannot measure the torque acting on it.
50. On page 680, the curl of \(x\hat{\mathbf{y}}\) was computed. Now consider the fields \(x\hat{\mathbf{x}}\) and \(y\hat{\mathbf{y}}\).
(a) Sketch these fields.
(b) Using the same technique of explicitly constructing a small square, prove that their curls are both zero. Do not use the component form of the curl; this was one step in deriving the component form of the curl.
51. If you watch a movie played backwards, some vectors reverse their direction. For instance, people walk backwards, with their velocity vectors flipped around. Other vectors, such as forces, keep the same direction, e.g., gravity still pulls down. An electric field is another example of a vector that doesn't turn around: positive charges are still positive in the time-reversed universe, so they still make diverging electric fields, and likewise for the converging fields around negative charges.
(a) How does the momentum of a material object behave under time-reversal?(solution in the pdf version of the book)
(b) The laws of physics are still valid in the time-reversed universe. For example, show that if two material objects are interacting, and momentum is conserved, then momentum is still conserved in the time-reversed universe.(solution in the pdf version of the book)
(c) Discuss how currents and magnetic fields would behave under time reversal. \hwhint{hwhint:timereversalem}
(d) Similarly, show that the equation \(d\mathbf{p}\propto\mathbf{E}\times\mathbf{B}\) is still valid under time reversal.
52. This problem is a more advanced exploration of the time-reversal ideas introduced in problem 51.
(a) In that problem, we assumed that charge did not flip its sign under time reversal. Suppose we make the opposite assumption, that charge does change its sign. This is an idea introduced by Richard Feynman: that antimatter is really matter traveling backward in time! Determine the time-reversal properties of \(\mathbf{E}\) and \(\mathbf{B}\) under this new assumption, and show that \(d\mathbf{p}\propto\mathbf{E}\times\mathbf{B}\) is still valid under time-reversal.
(b) Show that Maxwell's equations are time-reversal symmetric, i.e., that if the fields \(\mathbf{E}(x,y,z,t)\) and \(\mathbf{B}(x,y,z,t)\) satisfy Maxwell's equations, then so do \(\mathbf{E}(x,y,z,-t)\) and \(\mathbf{B}(x,y,z,-t)\). Demonstrate this under both possible assumptions about charge, \(q\rightarrow q\) and \(q\rightarrow -q\).
53. The purpose of this problem is to prove that the constant of proportionality \(a\) in the equation \(dU_m=aB^2 dv\), for the energy density of the magnetic field, is given by \(a=c^2/8\pi k\) as asserted on page 665. The geometry we'll use consists of two sheets of current, like a sandwich with nothing in between but some vacuum in which there is a magnetic field. The currents are in opposite directions, and we can imagine them as being joined together at the ends to form a complete circuit, like a tube made of paper that has been squashed almost flat. The sheets have lengths \(L\) in the direction parallel to the current, and widths \(w\). They are separated by a distance \(d\), which, for convenience, we assume is small compared to \(L\) and \(w\). Thus each sheet's contribution to the field is uniform, and can be approximated by the expression \(2\pi k\eta/c^2\).
(a) Make a drawing similar to the one in figure 11.2.1 on page 664, and show that in this opposite-current configuration, the magnetic fields of the two sheets reinforce in the region between them, producing double the field, but cancel on the outside.
(b) By analogy with the case of a single strand of wire, one sheet's force on the other is \(ILB_1\), were \(I=\eta w\) is the total current in one sheet, and \(B_1=B/2\) is the field contributed by only one of the sheets, since the sheet can't make any net force on itself. Based on your drawing and the right-hand rule, show that this force is repulsive.
For the rest of the problem, consider a process in which the sheets start out touching, and are then separated to a distance \(d\). Since the force between the sheets is repulsive, they do mechanical work on the outside world as they are separated, in much the same way that the piston in an engine does work as the gases inside the cylinder expand. At the same time, however, there is an induced emf which would tend to extinguish the current, so in order to maintain a constant current, energy will have to be drained from a battery. There are three types of energy involved: the increase in the magnetic field energy, the increase in the energy of the outside world, and the decrease in energy as the battery is drained. (We assume the sheets have very little resistance, so there is no ohmic heating involved.)(answer check available at lightandmatter.com)
(c) Find the mechanical work done by the sheets, which equals the increase in the energy of the outside world. Show that your result can be stated in terms of \(\eta\), the final volume \(v=wLd\), and nothing else but numerical and physical constants.(answer check available at lightandmatter.com)
(d) The power supplied by the battery is \(P=I\Gamma_E\) (like \(P=I\Delta V\), but with an emf instead of a voltage difference), and the circulation is given by \(\Gamma=-d\Phi_B/dt\). The negative sign indicates that the battery is being drained. Calculate the energy supplied by the battery, and, as in part c, show that the result can be stated in terms of \(\eta\), \(v\), and universal constants.(answer check available at lightandmatter.com)
(e) Find the increase in the magnetic-field energy, in terms of \(\eta\), \(v\), and the unknown constant \(a\).(answer check available at lightandmatter.com)
(f) Use conservation of energy to relate your answers from parts c, d, and e, and solve for \(a\).(answer check available at lightandmatter.com)
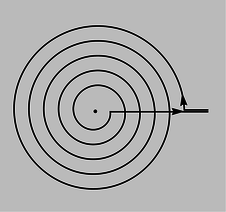
k / Problem 54.
54. Magnet coils are often wrapped in multiple layers. The figure shows the special case where the layers are all confined to a single plane, forming a spiral. Since the thickness of the wires (plus their insulation) is fixed, the spiral that results is a mathematical type known as an Archimedean spiral, in which the turns are evenly spaced. The equation of the spiral is \(r=w\theta\), where \(w\) is a constant. For a spiral that starts from \(r=a\) and ends at \(r=b\), show that the field at the center is given by \((kI/c^2w)\ln b/a\).(solution in the pdf version of the book)
Contributors and Attributions
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


