6.6: Degenerate Solutions
- Page ID
- 11579
This section can be omitted on a first reading.
At the event horizon of the Schwarzschild spacetime, the timelike and spacelike roles of the Schwarzschild \(r\) and \(t\) coordinates get swapped around, so that the signs in the metric change from +−−− to − + −−. In discussing cases like this, it becomes convenient to define a new usage of the term “signature,” as s = p − q, where p is the number of positive signs and q the number of negative ones. This can also be represented by the pair of numbers (p, q). The example of the Schwarzschild horizon is not too disturbing, both because the funny behavior arises at a singularity that can be removed by a change of coordinates and because the signature stays the same. An observer who free-falls through the horizon observes that the local properties of spacetime stay the same, with |s| = 2, as required by the equivalence principle.
But this only makes us wonder whether there are other examples in which an observer would actually detect a change in the metric’s signature. We are encouraged to think of the signature as something empirically observable because, for example, it has been proposed that our universe may have previously unsuspected additional spacelike dimensions, and these theories make testable predictions. Since we do not notice the extra dimensions in ordinary life, they would have to be wrapped up into a cylindrical topology. Some such theories, like string theory, are attempts to create a theory of quantum gravity, so the cylindrical radius is assumed to be on the order of the Planck length, which corresponds quantum-mechanically to an energy scale that we will not be able to probe using any foreseeable technology. But it is also possible that the radius is large — a possibility that goes by the name of “large extra dimensions” — so that we could see an effect at the Large Hadron Collider. Nothing in the formulation of the Einstein field equations requires a 3+1 (i.e., (1, 3)) signature, and they work equally well if the signature is instead 4+1, 5+1, . . . . Newton’s inverse-square law of gravity is described by general relativity as arising from the three-dimensional nature of space, so on small scales in a theory with n large extra dimensions, the 1/r2 behavior changes over to 1/r2+n, and it becomes possible that the LHC could produce microscopic black holes, which would immediately evaporate into Hawking radiation in a characteristic way.
So it appears that the signature of spacetime is something that is not knowable a priori, and must be determined by experiment. When a thing is supposed to be experimentally observable, general relativity tells us that it had better be coordinate-independent. Is this so? A proposition from linear algebra called Sylvester’s law of inertia encourages us to believe that it is. The theorem states that when a real matrix \(A\) is diagonalized by a real, nonsingular change of basis (a similarity transformation S−1AS), the number of positive, negative, and zero diagonal elements is uniquely determined. Since a change of coordinates has the effect of applying a similarity transformation on the metric, it appears that the signature is coordinate-independent.
This is not quite right, however, as shown by the following paradox. The coordinate invariance of general relativity tells us that if all clocks, everywhere in the universe, were to slow down simultaneously (with simultaneity defined in any way we like), there would be no observable consequences. This implies that the spacetime
\[ds^2 = −t \,dt^2 − d \ell^{2},\]
where
\[d \ell^{2} = dx^2 + dy^2 + dz^2,\]
is empirically indistinguishable from a flat spacetime. Starting from t = \(− \infty\), the positive gtt component of the metric shrinks uniformly, which should be harmless. We can indeed verify by direct evaluation of the Riemann tensor that this is a flat spacetime (problem 10). But for t > 0 the signature of the metric switches from + − −− to − − −−, i.e., from Lorentzian (|s| = 2) to Euclidean (|s| = 4). This is disquieting. For t < 0, the metric is a perfectly valid description of our own universe (which is approximately flat). Time passes, and there is no sign of any impending disaster. Then, suddenly, at some point in time, the entire structure of spacetime undergoes a horrible spasm. This is a paradox, because we could just as well have posed our initial conditions using some other coordinate system, in which the metric had the familiar form ds2 = dt2 −d\(\ell^{2}\). General relativity is supposed to be agnostic about coordinates, but a choice of coordinate leads to a differing prediction about the signature, which is a coordinate-independent quantity.
We are led to the resolution of the paradox if we explicitly construct the coordinate transformation involved. In coordinates (t, x, y, z), we have ds2 = −t dt2 − d\(\ell^{2}\). We would like to find the relationship between t and some other coordinate u such that we recover the familiar form ds2 = du2 −d\(\ell^{2}\) for the metric. The tensor transformation law gives
\[\begin{split} g_{tt} &= \left(\dfrac{\partial u}{\partial t}\right)^{2} g_{uu} \\ -t &= \left(\dfrac{\partial u}{\partial t}\right)^{2} \end{split}\]
with solution
\[u = \pm \frac{2}{3} t^{\frac{3}{2}}, \quad t < 0 \ldotp\]
There is no solution for t > 0.
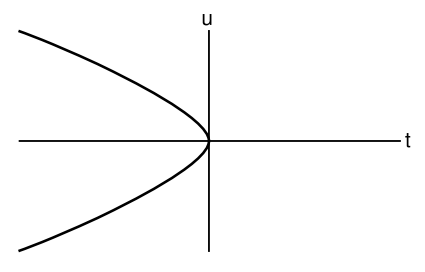
If physicists living in this universe, at t < 0, for some reason choose t as their time coordinate, there is in fact a way for them to tell that the cataclysmic event at t = 0 is not a reliable prediction. At t = 0, their metric’s time component vanishes, so its signature changes from + − −− to 0 − −−. At that moment, the machinery of the standard tensor formulation of general relativity breaks down. For example, one can no longer raise indices, because gab is the matrix inverse of gab, but gab is not invertible. Since the field equations are ultimately expressed in terms of the metric using machinery that includes raising and lowering of indices, there is no way to apply them at t = 0. They do not make a false prediction of the end of the world; they fail to make any prediction at all. Physicists accustomed to working in terms of the t coordinate can simply throw up their hands and say that they have no way to predict anything at t > 0. But they already know that their spacetime is one whose observables, such as curvature, are all constant with respect to time, so they should ask why this perfect symmetry is broken by singling out t = 0. There is physically nothing that should make one moment in time different than any other, so choosing a particular time to call t = 0 should be interpreted merely as an arbitrary choice of the placement of the origin of the coordinate system. This suggests to the physicists that all of the problems they’ve been having are not problems with any physical meaning, but merely problems arising from a poor choice of coordinates. They carry out the calculation above, and discover the u time coordinate. Expressed in terms of u, the metric is well behaved, and the machinery of prediction never breaks down.
The paradox posed earlier is resolved because Sylvester’s law of inertia only applies to a nonsingular transformation S. If S had been singular, then the S−1 referred to in the theorem wouldn’t even have existed. But the transformation from u to t has \(\frac{\partial t}{\partial u}\) = 0 at u = t = 0, so it is singular. This is all in keeping with the general philosophy of coordinate-invariance in relativity, which is that only smooth, one-to-one coordinate transformations are allowed. Someone who has found a lucky coordinate like u, and who then contemplates transforming to t, should realize that it isn’t a good idea, because the transformation is not smooth and one-to-one. Someone who has started by working with an unlucky coordinate like t finds that the machinery breaks down at t = 0, and concludes that it would be a good idea to search for a more useful set of coordinates. This situation can actually arise in practical calculations.
What about our original question: could the signature of spacetime actually change at some boundary? The answer is now clear. Such a change of signature is something that could conceivably have intrinsic physical meaning, but if so, then the standard formulation of general relativity is not capable of making predictions about it. There are other formulations of general relativity, such as Ashtekar’s, that are ordinarily equivalent to Einstein’s, but that are capable of making predictions about changes of signature. However, there is more than one such formulation, and they do not agree on their predictions about signature changes.


