6.5: Black Holes (Part 2)

Singularities can also occur without any blow-up in the curvature. An example of this is a conical singularity, Figure 6.3.2. (Cf. Figure 5.9.2) In 2+1-dimensional relativity, curvature vanishes identically in the case of a vacuum, and the only kind of curvature singularity we can have is a non-curvature singularity. Another example of a non-curvature singularity is provided by the Taub-NUT family of spacetimes, in which some lightlike geodesics spiral in toward a horizon, but tidal forces do not blow up at the horizon. There is no clear reason to expect that non-curvature singularities could actually exist in our universe, but neither is there any proof that they cannot be formed by natural processes.

Figure \(\PageIndex{2}\): A conical singularity. The cone has zero intrinsic curvature everywhere except at its tip. Geodesic 1 can be extended infinitely far, but geodesic 2 cannot; since the metric is undefined at the tip, there is no sensible way to define how geodesic 2 should be extended.

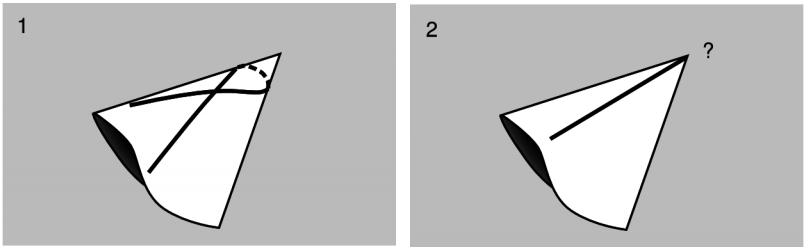
Example 4: A non-curvature singularity

Consider the metric

\[ds^{2} = \frac{1}{t} dt^{2} - t \,d \theta^{2}\]

in 1+1 dimensions, where \(\theta\) is an angle running around the circle. This is a simplified version of a Taub-NUT spacetime. Lightlike geodesics have ds = 0, so \(\frac{dt}{t}\) = ± d\(\theta\), and \(\theta\) = (const) ± ln(±t), where the two signs can be chosen independently. Single out the geodesic \(\theta\) = ln t, which is defined only for t > 0. It wraps around the circle infinitely many times as t goes to zero, and we would like to know whether it is incomplete there. If the affine parameter goes to infinity as t approaches zero, then the geodesic is not incomplete.

The nonvanishing Christoffel symbols are \(\Gamma^{t}_{tt} = − \frac{1}{2t}, \Gamma^{\theta}_{\theta t} = \Gamma^{\theta}_{t \theta} = \frac{1}{2t}\), and \(\Gamma^{t}_{\theta \theta} = \frac{t}{2}\) (Problem 3). The resulting geodesic equations are

\[\begin{split} \ddot{t} &= \frac{\dot{t}^{2}}{2t} - \frac{t}{2} \dot{\theta}^{2} \\ \ddot{\theta} &= - \frac{\dot{t}}{\dot{\theta}} t, \end{split}\]

where dots represent differentiation with respect to the affine parameter \(\lambda\). Implicit differentiation of the equation \(\theta\) = ln t gives \(\dot{\theta} = \frac{\dot{t}}{t}\), and plugging this in to the first geodesic equation results in \(\ddot{t}\)= 0. We can therefore take t = \(\lambda\). (We could also take t = a\(\lambda\) + b, which would result in a different and equally valid affine parameter.) If λ had gone to \(− \infty\) as t went to zero, then we would have demonstrated that the geodesic was complete. It approaches a finite limit instead, which suggests, but does not prove, that it is incomplete.

The change of coordinates \(\theta \rightarrow \theta\) − ln t allows the counterclockwise lightlike geodesics to be continued through t = 0. (Because this transformation is not a diffeomorphism, it is not just a renaming of points but an actual physical change in the structure of the spacetime; it is equivalent to cutting apart the halves with t < 0 and t > 0 and gluing them back together in a different way.) The corresponding geodesics in the clockwise direction, however, remain incomplete. A different change of coordinates extends the clockwise but not the counterclockwise ones. In all cases there are incomplete geodesics, so it still appears that we do have a singularity. Since curvature singularities don’t exist in less than 3+1 dimensions, this is a non-curvature singularity. (A calculation also shows that this particular spacetime is flat.)

A singularity is not considered to be a point or set of points in a spacetime; it’s more like a hole in the topology of the manifold. For example, the Big Bang didn’t occur at a point or set of points. A singularity represents a breakdown in the metric, and without a metric we may not even be able to tell the difference between one point and many. For more on these issues, see the discussions of boundary constructions in section 7.3. There is a sense in which a black hole singularity is not a thing at all, and has no definable characteristics; section 7.4.

Example 5: One point, or many?

Suppose I have a two-dimensional space with coordinates (u, v), and I ask you whether S = {(u, v)|v = 0} is a point or a curve, while refusing to divulge what metric I have in mind. You’d probably say S was a curve, and if the metric was ds² = du²+dv², you’d be right. On the other hand, if the metric was ds² = v² du² + dv², S would be a point.

This was an example where there were two possible metrics we could imagine. At a singularity, it’s even worse. There is no possible metric that we can extend to the singularity.

Because a singularity isn’t a point or a point-set, we can’t define its timelike or spacelike character in quite the way we would with, say, a curve. A timelike singularity, also referred to as a locally naked singularity, is one such that an observer with a timelike worldline can have the singularity sometimes in his future light-cone and sometimes in his past light-cone.¹⁸

Schwarzschild and Big Bang singularities are spacelike. (Note that in the Schwarzschild metric, the Schwarzschild r and t coordinates swap their timelike and spacelike characters inside the event horizon.) The definition of a timelike singularity is local. A timelike singularity would be one that you could have sitting on your desk, where you could look at it and poke it with a stick.

A naked singularity is one from which timelike or lightlike worldlines can originate and then escape to infinity. The Schwarzschild metric’s singularity is not naked. This notion is global.

Evidence Accumulating Against Cosmic Censorship

As of 2017, evidence is accumulating that cosmic censorship is false. Back in 1969 when Roger Penrose first formulated the hypothesis, relativists had been strongly influenced by a 1939 calculation by Oppenheimer and Snyder for the gravitational collapse of a uniform, spherical cloud of “dust,” meaning material particles that act like a pressureless ideal fluid (see example 1). (Cf. section 4.4 on the Tolman-Oppenheimer-Volkoff limit, derived earlier the same year.) Even though Oppenheimer and Snyder were too timid to continue the calculation past the formation of an event horizon, their result was not taken seriously for years, the notion of a runaway gravitational collapse being too distant from the state of the art in terms of observation. But later workers did complete the calculation. They found that a singularity developed, but that the horizon formed early enough to cloak it, so that no timelike or lightlike geodesic from the singularity could escape to a distant observer. This was consistent with a weak version of the cosmic censorship hypothesis, that a (globally) naked singularity cannot form from gravitational collapse.

But to interpret the result as evidence for cosmic censorship was misleading. With hindsight, there are clear Newtonian reasons to suspect that a perfectly homogeneous cloud has properties that are a little too special. In the Newtonian version the internal gravitational field is proportional to r. Starting from rest at r, a particle has to travel a distance r to reach the center, but since the acceleration is proportional to r, the time needed to reach the center is the same for all particles. There is a Newtonian singularity of infinite density, and this occurs at the same time for all particles, which is after the formation of a surface from which the escape velocity has any fixed value, such as c. Therefore in Newtonian terms, cosmic censorship holds, but it holds only because of the perfect homogeneity of the cloud.

In fact, the general-relativistic version of inhomogeneous gravitational collapse had already been worked out around 1933 by Lemaître, Tolman, and Bondi, again for the case of a spherical cloud, but now with a density profile \(\rho\)(r). This family of metrics, called the Lemaître-Tolman-Bondi metrics, is general enough to include models of cosmological expansion as well as models of local gravitational collapse. Tolman applied the collapse model to the formation of “nebulae,” i.e., galaxies, in the early universe, but did not follow the evolution of the collapse to its ultrarelativistic dénouement, as Oppenheimer and Snyder had. When one does so, dealing with some technical obstacles and imposing some constraints for physical reasonableness, it turns out that in most cases, the result is a locally naked singularity.¹⁹ That is, fine-tuning is required in order to produce something more like a standard black hole. It remains to be seen whether this holds true when the constraint of perfect spherical symmetry is relaxed.

This does not necessarily mean on the face of it that cosmic censorship is dead, since spacetimes with spherical symmetry are themselves finely tuned in some sense, but it is rather a dramatic development, since people had imagined for 75 years, based on the Oppenheimer-Snyder calculations for homogeneous dust, that a black hole was the generic result of runaway gravitational collapse. Cosmic censorship is in a sense impossible to disprove, since part of the research program is to find the most appropriate definition of the conjecture, but these results suggest that if it is to be true, then it has to be weakened so much as to be of little interest. In general, a meaningful definition of what it means to violate weak cosmic censorship should probably include something like the following ingredients.

1. The initial conditions do not make available an infinite amount of energy within a finite region.
2. The initial conditions do not contain singularities.
3. Incomplete lightlike geodesics can arrive at a distant observer.
4. Such a violation still occurs if we impose small perturbations on the initial data.
5. The forms of matter are physically realistic.

If we do not impose something like condition 1, then we can set up initial conditions that are of no interest because they are unrealistic. For this reason, one usually studies spacetimes that are asymptotically flat.²⁰ Condition 2 expresses the idea that any singularities that occur should be new ones formed by gravitational collapse. The censorship violation is expressed by condition 3. The notion of a distant observer can be further formalized by requiring that such a geodesic arrive at null infinity, I +; see p. 265. If 4 is omitted, then clear counterexamples to censorship are known. However, it is not known whether there is an appropriately rigorous way to define “small perturbations” here.²¹ Realistic matter fields, 5, are expected, for example, not to have negative mass.²²

Because weak cosmic censorship seems to be violated if described by these five conditions, people have started looking for additional conditions that could salvage the conjecture.

Wald²³ suggests adding a sixth requirement. He proposes that the types of matter be further restricted to ones having the property that if the metric is fixed, rather than dynamical as in general relativity, then no singularities occur. This seems to me to be much too strong a condition, and there are indications that it is not sufficient.

Note

²⁰ Asymptotic flatness was introduced informally in section 4.5 and is defined in detail in section 7.4. It may also be necessary to impose a requirement that the matter fields fall off at some rate as we go to infinity.

²¹ In technical terms, we do not have any topology or measure defined on the set of all possible initial conditions. In actual work to date, people have selected some set of possible initial conditions, described by some small number of adjustable parameters, and have then tried to test condition 4 using a seemingly natural topology and measure defined on the space of those parameters.

²² More rigorously, we expect them to satisfy suitable energy conditions, section 8.1.

Another proposal is along the following lines. When a naked singularity occurs, then we have a region of spacetime for which the singularity is inside the past lightcone. The lightlike surface constituting the boundary of this region is called a Cauchy horizon. An observer who passes beyond the Cauchy horizon can observe arbitrary information, i.e., phenomena not predicted by any laws of physics, and infinite fluxes of energy. Roger Penrose has, however, pointed out that in certain illustrative cases, there is a tendency for energy from the entire spacetime prior to the singularity to be focused onto the Cauchy horizon. The result could then be that such an observer is destroyed when passing through the Cauchy horizon. In other words, the Cauchy horizon actually turns into a singularity. Penrose’s mechanism appears to fail, however, for a spacetime with a positive cosmological constant, which is what we actually have in our universe.

Hawking Radiation

Radiation from Black Holes

Since event horizons are expected to emit blackbody radiation, a black hole should not be entirely black; it should radiate. This is called Hawking radiation. Suppose observer B just outside the event horizon blasts the engines of her rocket ship, producing enough acceleration to keep from being sucked in. By the equivalence principle, what she observes cannot depend on whether the acceleration she experiences is actually due to a gravitational field. She therefore detects radiation, which she interprets as coming from the event horizon below her. As she gets closer and closer to the horizon, the acceleration approaches infinity, so the intensity and frequency of the radiation grows without limit.

A distant observer A, however, sees a different picture. According to A, B’s time is extremely dilated. A sees B’s acceleration as being only ∼ 1/m, where m is the mass of the black hole; A does not perceive this acceleration as blowing up to infinity as B approaches the horizon. When A detects the radiation, it is extremely red-shifted, and it has the spectrum that one would expect for a horizon characterized by an acceleration a ∼ 1/m. The result for a 10-solar-mass black hole is T ∼ 10⁻⁸ K, which is so low that the black hole is actually absorbing more energy from the cosmic microwave background radiation than it emits.

Direct observation of black-hole radiation is therefore probably only possible for black holes of very small masses. These may have been produced soon after the big bang, or it is conceivable that they could be created artificially, by advanced technology. If blackhole radiation does exist, it may help to resolve the information paradox, since it is possible that information that goes into a black hole is eventually released via subtle correlations in the black-body radiation it emits.

Particle Physics

Hawking radiation has some intriguing properties from the point of view of particle physics. In a particle accelerator, the list of particles one can create in appreciable quantities is determined by coupling constants. In Hawking radiation, however, we expect to see a representative sampling of all types of particles, biased only by the fact that massless or low-mass particles are more likely to be produced than massive ones. For example, it has been speculated that some of the universe’s dark matter exists in the form of “sterile” particles that do not couple to any force except for gravity. Such particles would never be produced in particle accelerators, but would be seen in Hawking radiation. Based on present knowledge of particle physics, the main components of Hawking radiation, for all but the most microscopic black holes, are expected to be photons and gravitons, which would compete on roughly equal terms, depending on the angular momentum of the black hole.²⁴

Hawking radiation would violate many cherished conservation laws of particle physics. Let a hydrogen atom fall into a black hole. We’ve lost a lepton and a baryon, but if we want to preserve conservation of lepton number and baryon number, we cover this up with a fig leaf by saying that the black hole has simply increased its lepton number and baryon number by +1 each. But eventually the black hole evaporates, and the evaporation is probably mostly into zero-mass particles such as photons. Once the hole has evaporated completely, our fig leaf has evaporated as well. There is now no physical object to which we can attribute the +1 units of lepton and baryon number.

Black-hole Complementarity

A very difficult question about the relationship between quantum mechanics and general relativity occurs as follows. In our example above, observer A detects an extremely red-shifted spectrum of light from the black hole. A interprets this as evidence that the space near the event horizon is actually an intense maelstrom of radiation, with the temperature approaching infinity as one gets closer and closer to the horizon. If B returns from the region near the horizon, B will agree with this description. But suppose that observer C simply drops straight through the horizon. C does not feel any acceleration, so by the equivalence principle C does not detect any radiation at all. Passing down through the event horizon, C says, “A and B are liars! There’s no radiation at all.” A and B, however, C see as having entered a region of infinitely intense radiation. “Ah,” says A, “too bad. C should have turned back before it got too hot, just as I did.” This is an example of a principle we’ve encountered before, that when gravity and quantum mechanics are combined, different observers disagree on the number of quanta present in the vacuum. We are presented with a paradox, because A and B believe in an entirely different version of reality that C. A and B say C was fricasseed, but C knows that that didn’t happen. One suggestion is that this contradiction shows that the proper logic for describing quantum gravity is nonaristotelian, as described in section 2.3. This idea, suggested by Susskind et al., goes by the name of black-hole complementarity, by analogy with Niels Bohr’s philosophical description of wave-particle duality as being “complementary” rather than contradictory. In this interpretation, we have to accept the fact that C experiences a qualitatively different reality than A and B, and we comfort ourselves by recognizing that the contradiction can never become too acute, since C is lost behind the event horizon and can never send information back out.

Black Holes in d Dimensions

It has been proposed that our universe might actually have not d = 4 dimensions but some higher number, with the d − 4 “extra” ones being spacelike, and curled up on some small scale \(\rho\) so that we don’t see them in ordinary life. One candidate for such a scale \(\rho\) is the Planck length, and we then have to talk about theories of quantum gravity such as string theory. On the other hand, it could be the 1 TeV electroweak scale; the motivation for such an idea is that it would allow the unification of electroweak interactions with gravity. This idea goes by the name of “large extra dimensions” — “large” because \(\rho\) is bigger than the Planck length. In fact, in such theories the Planck length is the electroweak unification scale, and the number normally referred to as the Planck length is not really the Planck length.²⁵

In d dimensions, there are d−1 spatial dimensions, and a surface of spherical symmetry has d − 2. In the Newtonian weak-field limit, the density of gravitational field lines falls off like \(\frac{m}{r^{d−2}}\) with distance from a source m, and we therefore find that Newton’s law of gravity has an exponent of −(d − 2). If d ≠ 3, we can integrate to find that the gravitational potential varies as \(\Phi\) ∼ −mr^−(d−3). Passing back to the weak-field limit of general relativity, the equivalence principle dictates that the g_tt term of the metric be approximately 1 + 2\(\Phi\), so we find that the metric has the form

\[ds^{2} \approx (1 − 2mr^{−(d−3)}) dt^{2} − (\ldots) dr^{2} − r^{2} d \theta^{2} − r^{2} \sin^{2} \theta \,d \phi^{2} \ldotp\]

This looks like the Schwarzschild form with no other change than a generalization of the exponent, and in fact Tangherlini showed in 1963 that for d > 4, one obtains the exact solution simply by applying the same change of exponent to g_rr as well.²⁶

If large extra dimensions do exist, then this is the actual form of any black-hole spacetime for r << \(\rho\), where the background curvature of the extra dimensions is negligible. Since the exponents are all changed, gravitational forces become stronger than otherwise expected at small distances, and it becomes easier to make black holes. It has been proposed that if large extra dimensions exist, microscopic black holes would be observed at the Large Hadron Collider. They would immediately evaporate into Hawking radiation, with an experimental signature of violating the standard conservation laws of particle physics. As of 2010, the empirical results seem to be negative.²⁷

The reasoning given above fails in the case of d = 3, i.e., 2+1- dimensional spacetime, both because the integral of r⁻¹ is not r⁰ and because the Tangherlini-Schwarzschild metric is not a vacuum solution. As shown in problem 12, there is no counterpart of the Schwarzschild metric in 2+1 dimensions. This is essentially because for d = 3 mass is unitless, so given a source having a certain mass, there is no way to set the distance scale at which Newtonian weak-field behavior gives way to the relativistic strong field. Whereas for d ≥ 4, Newtonian gravity is the limiting case of relativity, for d = 3 they are unrelated theories. In fact, the relativistic theory of gravity for d = 3 is somewhat trivial. Spacetime does not admit curvature in vacuum solutions,²⁸ so that the only nontrivial way to make non-Minkowski 2+1-dimensional spacetimes is by gluing together Minkowski pieces in various topologies, like gluing pieces of paper to make things like cones and M¨obius strips. 2+1-dimensional gravity has conical singularities, but not Schwarzschild-style ones that are surrounded by curved spacetime.

If black-hole solutions exist in d dimensions, then one can extend such a solution to d+1 dimensions with cylindrical symmetry, forming a “black string.” The nonexistence of d = 3 black holes implies that black string solutions do not exist in our own d = 4 universe. However, different considerations arise in a universe with a negative cosmological constant. There are then 2+1-dimensional solutions known as BTZ black holes.²⁹ Since our own universe has a positive cosmological constant, not a negative one, we still find that black strings cannot exist.

References

¹⁸ Penrose, Gravitational radiation and gravitational collapse; Proceedings of the Symposium, Warsaw, 1973. Dordrecht, D. Reidel Publishing Co. pp. 82-91, free online at adsabs.harvard.edu/full/1974IAUS...64...82P

¹⁹ Joshi and Malafarina, arxiv.org/abs/1405.1146

²³ “Gravitational Collapse and Cosmic Censorship,” arxiv.org/abs/gr-qc/ 9710068

²⁴ Dong, arxiv.org/abs/1511.05642

²⁵ Kanti, arxiv.org/abs/hep-ph/0402168

²⁶ Emparan and Reall, “Black Holes in Higher Dimensions,” relativity. livingreviews.org/Articles/lrr-2008-6/

²⁷ http://arxiv.org/abs/1012.3375

²⁸ arxiv.org/abs/gr-qc/0503022v4

²⁹ arxiv.org/abs/gr-qc/9506079v1