7.2: Transformation of Vectors
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Explain how to transform vectors
Now suppose we want to transform a vector whose components are expressed in the (T,X) coordinates into components expressed in (t,x).
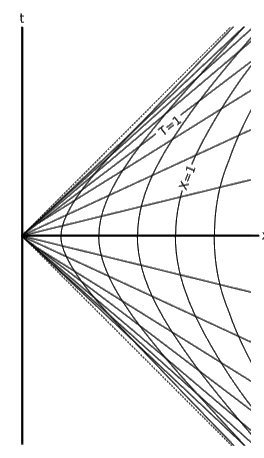
Our most basic example of a vector is a displacement (∆T,∆X), and if we make this an infinitesimal (dT,dX) then we don’t need to worry about the fact that the chart in figure 7.2.1 has curves on it — close up, curves look like straight lines.1 If we think of the coordinate t as a function of two variables, t=t(T,X), then t is changing for two different reasons: its first input T changes, and also its second input X. If t were only a function of one variable t(T), then the change in t would be given simply by the chain rule, dT=dt/dTdT. Since it actually has two such reasons to change, we add the two changes:
dt=∂t∂TdT+∂t∂XdX
The derivatives are partial derivatives, and these derivatives exist because, as we will always assume, the change of coordinates is smooth. An exactly analogous expression applies for dx.
dx=∂x∂TdT+∂x∂XdX
Before we carry out the details of this calculation, let’s stop and note that the results so far are completely general. Since we have so far made no use of the actual equations for this particular change of coordinates, these expressions would apply to any such transformation, including the special cases we’ve encountered so far, such as Lorentz transformations and scaling. (For example, if we’d been scaling by a factor α, then all of the partial derivatives would simply have equaled α.). Furthermore, our definition of a vector is that a vector is anything that transforms like a vector. Since we’ve established that the rules above apply to a displacement vector, we conclude that they would also apply to any other vector, say an energy-momentum vector.
Returning to this specific example, application of the facts
\frac{\mathrm{d} \sinh u}{\mathrm{d} u} = \cosh u\; \; \text{and}\; \; \frac{\mathrm{d} \cosh u}{\mathrm{d} u} = \sinh u
tells us that the vector (dT,dX) is transformed to:
(dt,dx) = (X \cosh T dT + \sinh T dX ,\; X \sinh T dT + \cosh T dX)
As an example of how this applies universally to any type of vector, suppose that the observer aboard a spaceship with world-line (T,X) = (τ,1) has a favorite paperweight with mass m. According to measurements carried out aboard her ship, its energy-momentum vector is:
(p_T,p_X) = (m,0)
In the unaccelerated coordinates, this becomes
\begin{align*} (p_t,p_x) &= (X \cosh T p_T + \sinh T p_X ,\; X \sinh T p_T + \cosh T p_X)\\ &= (mX\cosh T,\; mX\sinh T)\\ &= (m\cosh \tau ,\; m\sinh \tau ) \end{align*}
Since the functions cosh and sinh behave like e^x for large x, we find that after the astronaut has spent a reasonable amount of proper time τ accelerating, the paperweight’s mass-energy and momentum will have grown to the point where it’s an awesome weapon of mass destruction, capable of obliterating an entire galaxy.
References
1 Here we make use of the fact that the change of coordinate was smooth, i.e., a diffeomorphism. Otherwise the curves could have kinks in them that would still look like kinks under any magnification.


