7.E: Coordinates (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Q1
Example 7.4.2 discussed polar coordinates in the Euclidean plane. Use the technique demonstrated in section 7.3 to find the metric in these coordinates.
Q2
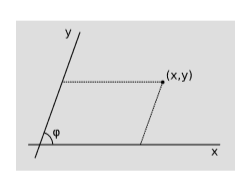
Oblique Cartesian coordinates are like normal Cartesian coordinates in the plane, but their axes are at at an angle φ≠π/2 to one another. Show that the metric in these coordinates is
ds2=dx2+dy2+2cosφdxdy
Q3
Let a 3-plane U be defined in Minkowski coordinates by the equation x=t. Is this plane spacelike, timelike, or lightlike? Find a covector S→ that is normal to U in the sense described in section 7.6, describing it in terms of its components. Compute the vector S, also in component form. Verify that S→S=0. Show that →S is tangent to M.
Q4
For the oblique Cartesian coordinates defined in problem Q2, use the determinant of the metric to show that the Levi-Civita tensor is
ϵ=(0sinφ−sinφ0)
Q5
Use the technique demonstrated in Example 7.6.6, to find the volume of the unit sphere.


